7.剛体
この記事では剛体全般について解説しています。
内容としては、剛体と質点の違いや、力のモーメントの計算方法、物体の重心の求め方などになります。
物体の重心も、力のモーメントとつりあいから求める方法と、座標から求める方法を解説しています。
また、数学的にはどのように重心を求めるかについても紹介しています。
練習問題の方で解説しているものもありますので、そちらもご覧ください。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
→剛体
Twitterアカウント→@roke_blog
目次
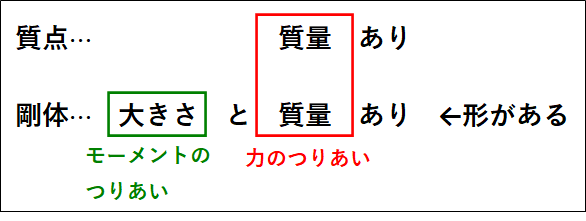
1.剛体と質点
力についての解説記事で扱ってきた物体は、全て\(\textcolor{red}{\bf{質点}}\)となります。
しかし、今回は\(\textcolor{red}{\bf{剛体}}\)というものを扱っていきます。
"質点"と"剛体"の違いは、以下のようになります。
質点:
形や大きさを無視し、質量が1点に集中したもの
剛体:
形や大きさを持ち、力を加えても変形しない物体(回転についても考える必要がある)
2.力のモーメント(トルク)
物体にはたらく力の大きさ\(F\)と、回転軸から力の作用線におろした垂線の長さ\(l\)(うでの長さ)との積は、剛体を回転軸まわりに回転させようとする能力の大きさを表しています。
これを\(\textcolor{red}{\bf{力のモーメント}}\)といいます。
力については、大きいほど回転しやすいということが分かると思います。
うでの長さについては、例えばスパナなど(扱ったことがないかもしれませんが)何かを回したいときに、なるべく遠くをもって回転させようと力を加えると、楽に回せるという経験があるかもしれません。
力のモーメントの正負は、"反時計回りを正、時計回りを負"とします。
これは、三角関数において単位円上の角度\(\theta\)の正負とおなじ考えとなります。
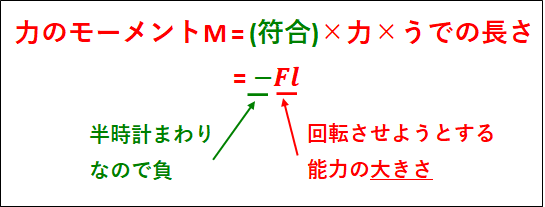
以上のことから、力のモーメント\(M\)は
\(M={\bf{(符合)×力×うでの長さ}}\)
で表されます。
単位は、力の単位である\(N\)と長さの単位である\(m\)を掛けて、
\(\displaystyle{\bf{\begin{eqnarray}{\bf{力×長さ}}&=&N×m\\\\&=&N・m\end{eqnarray}}}\)
から、\(N・m\)(ニュートンドットメートル)となります。
下記に、力のモーメントの例を載せておきます。
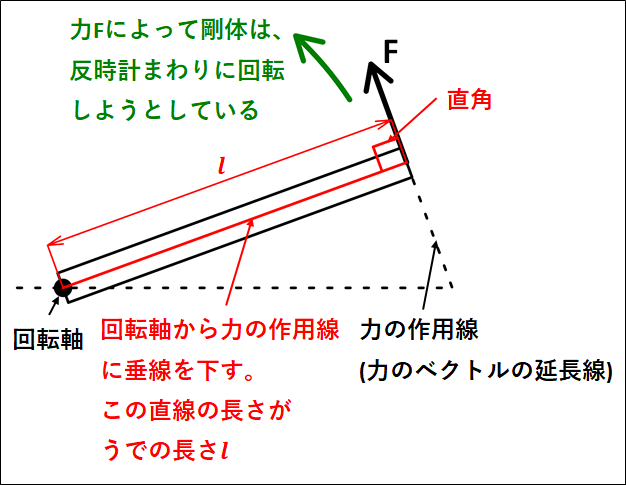
上図の場合、力\(F\)による力のモーメント\(M\)は
\(\displaystyle{M=-Fl}\)
となります。
回転の方向は、回転軸をピンで止め、かかっている力の方向に物体をはじいたときに回る方向となります。
3.剛体のつりあい
剛体は質点と異なり形と大きさをもつので、回転についてのつりあい(モーメントのつりあい)も考える必要があります。
モーメントがつりあう(回転しない)条件は、剛体にかかっている力のモーメントの和が\(0\)というものになります。
物体に複数の力がかかっており、この力によるモーメントをそれぞれ
\(M_1,M_2,M_3,\cdots\)
とすると、モーメントのつりあいの式は
\(M_1+M_2+M_3+\cdots=0\)
となります。
モーメントのつりあいを考える際には、回転軸を設定する必要がありますが、問題文で特に指定されていなければ、どこに設定してもよいです。
4.剛体にはたらく力の合成
定規やコンパスを使わずに、剛体にかかっている合力とその作用点を求めるには、
①力の大きさだけの和を考える
②力のはたらく位置を求める
\(\textcolor{green}{\bf{(モーメントが等しい)}}\)
という操作を行います。
具体的にどのように求めるかについては、練習問題の方で解説します。
5.偶力
\(\textcolor{red}{\bf{同じ大きさ}}\)で\(\textcolor{red}{\bf{反対向き}}\)の\(\textcolor{red}{\bf{平行}}\)な2力は、物体を移動させるはたらきはありませんが、物体を回転させるはたらきはもちます。
このような1組の力を"\(\textcolor{red}{\bf{偶力}}\)"といいます。
また、この2力の任意の点まわりの力のモーメントの和\(M^{\prime}\)を\(\textcolor{red}{\bf{偶力モーメント}}\)といいます。
例として、下図のような状況を考えます。
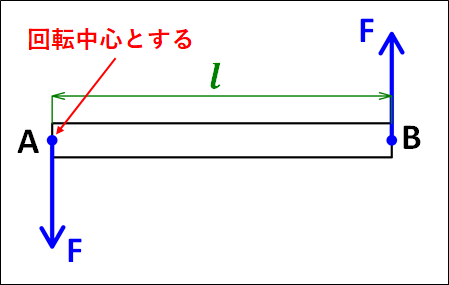
上図は力\(F\)が"同じ大きさ"、"反対向き"、"平行"に働いているので"偶力"となります。
力の和と、モーメントの和を実際に計算してみます。
\(\bf{\underline{○力の和}}\)
力は上下方向にかかっているので、どちらを正にとっても良いですが上向きを正としておきます。
そうすると、\(A\)点にかかっている力は\(-F\)、\(B\)点にかかっている力は\(+F\)となります。
なので、これらの力の和は
\((-F)+(+F)=0\)
となります。
上式の結果から、上下方向の力の和(合力)は\(0\)なので、つりあっていることがわかります。
このことから、物体を移動させるはたらきがないことが分かります。
\(\bf{\underline{○モーメントの和}}\)
次に、モーメントの和を考えていきます。
回転中心は、どこにとっても良いですが点\(A\)としておきます。
そうすると、点\(A\)を回転中心としたときの点\(A\)部分にかかっている力のモーメントは、うでの長さが\(0\)となるので
\(F×0\)
点\(A\)を回転中心としたときの点\(B\)部分にかかっている力のモーメントは、うでの長さが\(l\)、点\(A\)にピンをさして点\(B\)部分にかかっている力の方向に物体をはじくと反時計まわりに回転するので、符合は正となります。
よって、
\((+)F×l\)
となります。
これらモーメントの和を計算すると
\((F×0)+(+Fl)=+Fl\)
この\(+Fl\)が\(\textcolor{red}{\bf{偶力モーメント}}\)となります。
この場合、上記の偶力モーメントは剛体を反時計まわりに回転させようとするはたらきをもっています。(符合がプラスなので)
6.重心
剛体を無数の小さな部分の集まりと考えると、この小さな各部分には重力がはたらいています。
この\(\textcolor{red}{\bf{各部分にはたらく重力の和}}\)を、その物体の"\(\textcolor{red}{\bf{重心}}\)"といいます。
※
質点では、大きさがないので重力は1点にしかはたらかない
また、物体を重心で支えれば、回転せずにつりあうので、"重心は物体全体の全質量が集まっている点とみなすこともできます"。
\(\bf{\underline{○重心の求め方}}\)
\(\bf{i)モーメントと力のつりあいで考える}\)
\(x\)軸上に質量がそれぞれ\(m_1,m_2,m_3\)の物体があるとします。
この物体の原点(回転中心)からの距離をそれぞれ\(x_1,x_2,x_3\)とします。
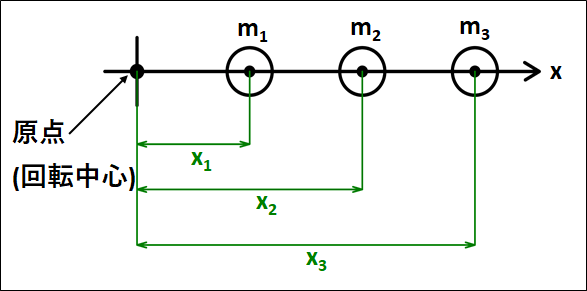
\(m_1,m_2,m_3\)にはそれぞれ重力がかかっており、重心では物体が回転せずにつりあうので、原点から重心までの距離を\(x_g\)、重心で支えている力を\(F\)とします。
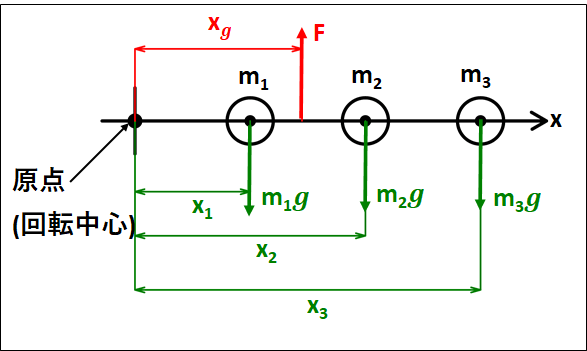
上図より、力のつりあいから
\(\displaystyle{\begin{eqnarray}F&=&m_1g+m_2g+m_3g\\\\&=&(m_1+m_2+m_3)g\cdots①\end{eqnarray}}\)
モーメントのつりあいから
\(\displaystyle{\small{\begin{eqnarray}&&(-m_1gx_1)+(-m_2gx_2)+(-m_3gx_3)+(+Fx_g)=0\\\\\Leftrightarrow&&Fx_g=(m_1x_1+m_2x_2+m_3x_3)g\cdots②\end{eqnarray}}}\)
\(①\)を\(②\)に代入して、
\(\displaystyle{\begin{eqnarray}&&(m_1+m_2+m_3)g・x_g=(m_1x_1+m_2x_2+m_3x_3)g\\\\\Leftrightarrow&&x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}\end{eqnarray}}\)
上記が回転中心からの重心の距離の公式になります。(物体が3つの場合)
\(\textcolor{green}{\bf{重心の公式}}\)
\(\displaystyle{\textcolor{green}{x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}}}\)
公式を、文字で表すと
\(\displaystyle{\bf{(重心の距離)=\frac{各物体の質量×各物体の距離 の和}{全質量}}}\)
となります。
上記は、物体が3つの場合ですが、4つや5つになった場合でも、分子に4つめや5つめの(質量×うでの長さ)を足していき、分母に4つや5つめの質量を足すと重心を求めることができます。
また、今回は\(x\)軸上(同一直線上)に並んだ物体に関して求めましたが、この場合(y)軸方向のうでの長さが\(0\)となるので、\(y\)軸に関して重心を求めると\(0\)となります。
よって、物体の重心は\(x\)軸からの距離が\(0\)の部分、すなわち\(x\)軸上にあるということになりますが、\(y\)軸方向にも物体がある場合、上記の公式を\(y\)軸方向の物体に関して立てることで、\(y\)軸方向の重心を求めることができます。
\(\bf{ii)座標で考える}\)
重心は、物体の全質量が集まっている点であるとみなせます。
また、重心ではモーメントがつりあうので、以下のことが成り立ちます。
\(\small{\bf{(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和}}\)
上式を念頭において、下図のような状況を考えます。
3つの物体は、質量がそれぞれ\(m_1,m_2,m_3\)とします。
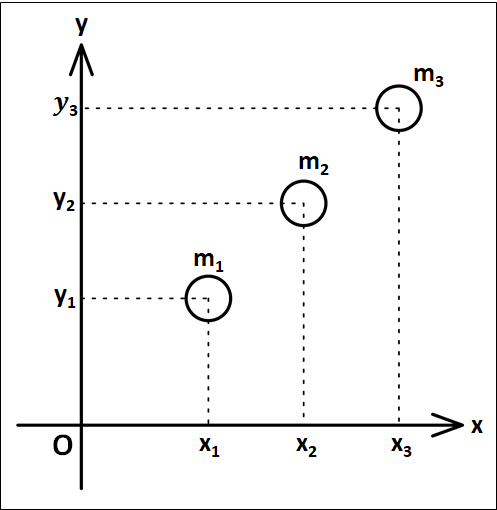
上図において、重心の\(x\)座標を\(x_g\)、\(y\)座標を\(y_g\)とします。
\(\small{\bf{(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和}}\) から、
\(x\)軸方向の重心座標\(x_g\)は
\(Mx_g=m_1x_1+m_2x_2+m_3x_3\)
ここで\(M\)は全質量で、\(M=m_1+m_2+m_3\)です。
これを先ほどの式に代入して、
\(\displaystyle{\begin{eqnarray}&&(m_1+m_2+m_3)x_g=m_1x_1+m_2x_2+m_3x_3\\\\\Leftrightarrow&&x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}\end{eqnarray}}\)
となります。
同様にして、\(y\)軸方向の重心座標\(y_g\)は、
\(\displaystyle{\begin{eqnarray}&&My_g=m_1y_1+m_2y_2+m_3y_3\\\\\Leftrightarrow&&(m_1+m_2+m_3)y_g=m_1y_1+m_2y_2+m_3y_3\\\\\Leftrightarrow&&y_g=\frac{m_1y_1+m_2y_2+m_3y_3}{m_1+m_2+m_3}\end{eqnarray}}\)
となります。
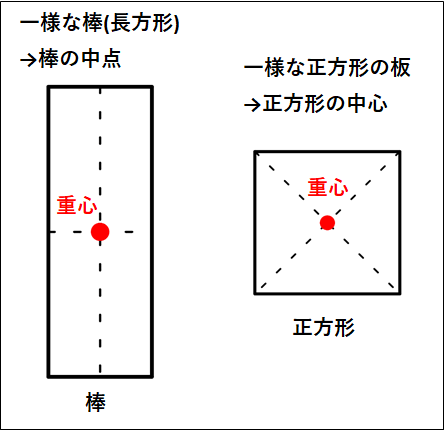
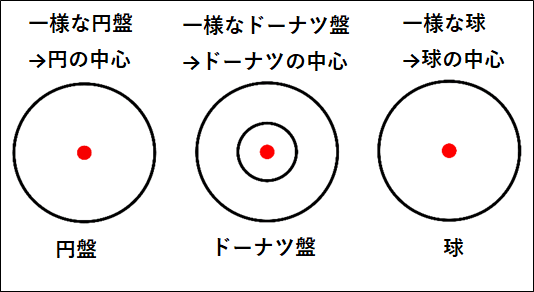
\(\bf{\underline{代表的な一様な物体の重心}}\)
代表的な一様な物体の重心位置を載せておきます。
だいたい物体の中心になるので覚えれないことはないと思います。
7.一様な棒と半球の重心(余談)
興味がない人は読み飛ばしていただいてかまいません。
積分を用いるので、積分に関してはこちらも参考にしてください
→積分法
→積分法の応用
※
大学的に…
一様な棒の重心はどう求めるのか?
\(\bf{\underline{○一様な棒の重心}}\)
以下のように座標を設定します。
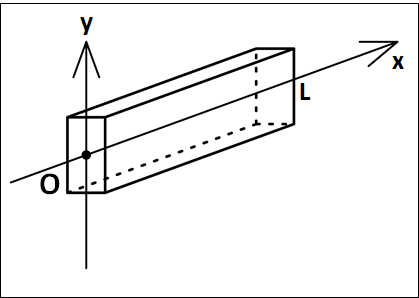
真横から見ると、次のようになります。
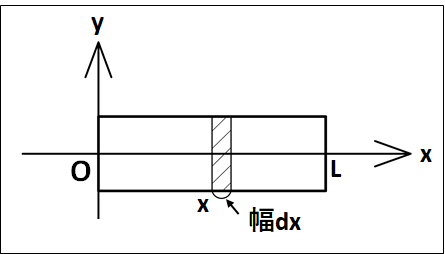
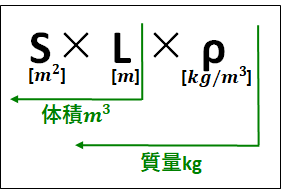
棒の断面積を\(S[m^2]\)、棒の長さを\(L[m]\)、棒の密度を\(ρ[kg/m^3]\)とします。
このとき、棒の全質量\(M\)は
\(M=S[m^2]×L[m]×ρ[kg/m^3]=SLρ[kg]\)
となります。
横から見た図のように、原点から\(x\)だけ離れた部分の微小幅\(dx\)部分の質量は、
\(S[m^2]×dx[m]×ρ[kg/m^3]=ρSdx[kg]\)
となります。
これより、微小部分の(質量×座標)は
\(ρSdx×x=ρSxdx\)
です。
これを\(x=0\)から\(x=L\)まで足すと、(各物体の質量×各物体の座標)の和、となり
\(\displaystyle{\int_0^L{ρSx}dx}\)
と表されます。
以上から、
(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和
を用いて、重心座標を\(x_g\)とすると、
\(\displaystyle{\begin{eqnarray}&&M×x_g=\int_0^L{ρSx}dx\\\\\Leftrightarrow&&SLρ×x_g=ρS\int_0^L{x}dx\\\\\Leftrightarrow&&L×x_g=\left[\frac{1}{2}x^2\right]_0^L\\\\\Leftrightarrow&&Lx_g=\frac{1}{2}L^2\\\\\Leftrightarrow&&x_g=\frac{1}{2}L\end{eqnarray}}\)
以上のことから、\(x\)軸方向の重心は、棒の中央が重心となることが分かります。
(全体の長さ\(L\)の半分の位置が重心)
\(\bf{\underline{○半球の重心}}\)
半径が\(r\)の半球の重心を求めてみます。
以下のように座標を設定し、\(y\)軸方向の重心である\(y_g\)について考えてみます。
半球は一様で、密度は\(ρ[kg/m^3]\)とします。
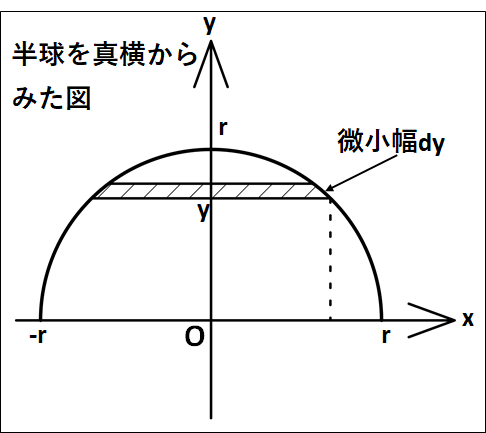
ここで、半径が\(r\)である円の方程式は
\(x^2+y^2=r^2\)
です。
図から、\(y\)座標の値が\(y\)である部分の\(x\)座標は、
\(\displaystyle{\begin{eqnarray}&&x^2+y^2=r^2\\\\\Leftrightarrow&&x^2=r^2-y^2\end{eqnarray}}\)
より、
\(x=±\sqrt{r^2-y^2}\)
これが、これから考える微小部円盤の、円の半径となります。
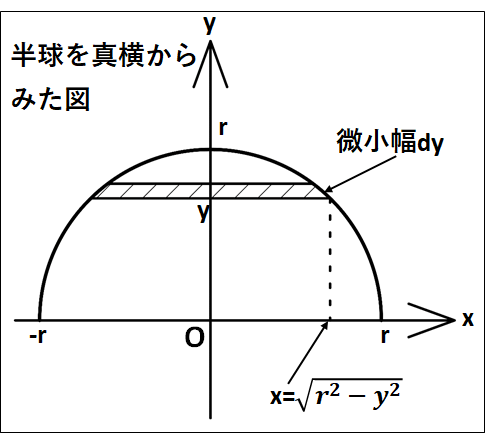
次に、微小幅\(dy\)部分の円盤の質量を考えていきます。
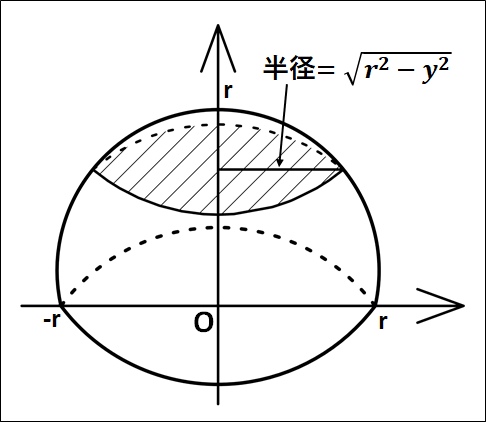
斜線部の円の半径は、先ほど求めた\(\displaystyle{\sqrt{r^2-y^2}}\)となります。
厚さ\(dy\)で半径が\(\displaystyle{\sqrt{r^2-y^2}}\)の微小円盤の質量は(円の面積×厚さ×密度)から、
\(\displaystyle{\begin{eqnarray}&&\pi{x^2}・dy・ρ\\\\=&&\pi{ρ}(r^2-y^2)dy\end{eqnarray}}\)
これより、(質量×\(y\)座標)は、
\(\displaystyle{\pi{ρ}(r^2-y^2)ydy}\)
となります。
全質量\(M\)は、球の質量の半分なので、(体積×密度÷2)から
\(\displaystyle{\begin{eqnarray}M&=&\frac{4\pi{r^3}}{3}・ρ×\frac{1}{2}\\\\&=&\frac{2}{3}\pi{ρ}r^3\end{eqnarray}}\)
以上から、一様な棒の重心を求めたときと同様にして、
(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和
を用いて
\(\displaystyle{\begin{eqnarray}&&M・y_g=\int_0^r{\pi{ρ}(r^2-y^2)y}dy\\\\\Leftrightarrow&&\frac{2}{3}\pi{ρ}r^3y_g=\pi{ρ}\int_0^r{(r^2y-y^3)}dy\\\\\Leftrightarrow&&\frac{2}{3}r^3y_g=\left[\frac{1}{2}r^2y^2-\frac{1}{4}y^4\right]_0^r\\\\\Leftrightarrow&&\frac{2}{3}r^3y_g=\frac{1}{2}r^4-\frac{1}{4}r^4=\frac{1}{4}r^4\\\\\Leftrightarrow&&y_g=\frac{3}{8}r\end{eqnarray}}\)
となります。
6-1.力の見つけ方
力とベクトルの記事で解説した内容の練習問題となります。
特に、物体にかかっている力の見つけ方や書き方の問題となっています。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、力のはたらきとつりあい記事で解説していなかった補足内容があれば、この記事に載せています。
問題の中でも特に、問題5~8は、繰り返し解いて完答できるようにしてください。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
- 1.問題1(力の描き方見つけ方)
- 2.問題2(力の描き方見つけ方)
- 3.問題3(作用・反作用の法則)
- 4.問題4(「つりあいの力」と「作用・反作用の力」の違い)
- 5.問題5(力の描き方見つけ方)
- 6.問題6(力の描き方見つけ方)
- 7.問題7(力の描き方見つけ方)
- 8.問題8(力の描き方見つけ方)
1.問題1(力の描き方見つけ方)
\(\underline{\bf{問題1}}\)
下図のように、物体に左向きの力Fを加えても動かないとき、物体は水平方向にどのような力を受けているか。
\(\underline{\bf{解答1}}\)
問題文に動かないと書いてあることから、力がつりあっていることが分かります。
(力がつりあっていない場合は動く)
このことから今、物体には左向きにFの力がかかっているので、つりあうためには右向きの力が必要であることが想像できます。
物体にかかっている接触力を見つけるには、物体をなでまわしたときに、あたってところに力がはたらいています。
今回、物体をなでまわしてみると、物体は地面とあたっていることが分かります。
地面が粗いか滑らかであるかの記述はありませんが、物体は力Fによって左向きに動こうとしているので、静止するためには、地面と物体の間にはその動きを妨げる向きにはたらく右向きの力である摩擦力がはたらいていると想像できます。
よって、この物体は水平方向に力Fと摩擦力を受けていることになります。
ちなみに、物体にかかっている全ての力は以下のようになります。
〇重力\(mg\)←"非接触力"であり、常に物体にかかっている。
〇垂直抗力N←物体は地面と接しており、地面から垂直に物体を貫く方向にかかる"接触力"。
〇力F←問題文の設定にある、物体に左向きにかかっている"接触力"。
〇摩擦力f←地面と物体の間にかかっている"接触力"で、物体の動きを妨げる向きにはたらく。
また上図と物体は動かない(物体にはたらく力がつりあっている)ことから、水平方向だけでなく鉛直方向に関しても、垂直抗力Nと重力\(mg\)がつりあっていることがわかります。
水平方向(左右方向)では、力Fと摩擦力fがつりあっていることで、物体は左右方向には動かず、鉛直方向(上下方向)には垂直抗力Nと重力\(mg\)がつりあっていることで、物体は上下方向には動かないことになります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・物体が動かない
→"力がつりあっている"はず
・接触力は、物体をなでまわしたときにあたった部分にはたらいている
2.問題2(力の描き方見つけ方)
\(\underline{\bf{問題2}}\)
下図のようになめらかな床の上に置かれた物体がある。
この物体にはばねと糸が取り付けられており、ばねの他端は壁に固定してある。
糸を水平に引き、ばねがのびた状態で物体が静止しているとき、物体が受けている力を全て答え、図示せよ。
\(\underline{\bf{解答2}}\)
物体には常に非接触力である、"重力"がかかっています。
重力の向きは、地球の中心方向(鉛直下向き)となります。
また、接触力を見つけるには、注目している物体の表面をなでまわします。
なでまわした際にぶつかる部分があれば、そこに力がはたらいています。
今回物体をなでまわしてみると、糸と床とばねにぶつかるので、この部分に力がはたらいていることが分かります。
次にそれぞれの部分にかかっている力についてみていきます。
〇物体と糸の接触部分にかかっている力
この部分の張力をTとすると、力は糸を引っ張ったときに抜ける方向にはたらきます。
今回の場合は、糸を引っ張ると右向きに抜けるので右向きに力がかかります。
〇物体と床の接触部分にかかっている力
この部分には抗力がはたらいています。
抗力には、垂直抗力と摩擦力がありますが、今回床はなめらかなので摩擦力ははたらいていません。
垂直抗力の方向は、接触面から垂直に自分を貫く方向にはたらきます。
今回の場合は鉛直上向きに力がかかっています。
この垂直抗力をNとします。
〇物体とばねの接触部分にかかっている力
ばねの弾性力は、ばねの伸びや縮みと逆方向にかかります。(ばねが元に戻ろうとする方向にかかる)
今回、ばねは伸びているので縮もうとする方向である左向きにかかります。
また、ばねの弾性力の"大きさ"はばねの伸びや縮みの大きさに比例し、比例定数をばね定数といいます。
ばねの伸びや縮みを\(x\)、ばね定数をkとすると、弾性力の大きさは\(kx\)と表せます。
以上より、それぞれの物体にはたらいている力を図示すると、下図のようになります。
これより、物体が受けている力は
・重力
・糸による張力
・床からの垂直抗力
・ばねの弾性力
となります。
ちなみに、物体が静止していることから、つりあいの式を立てると下記のようになります。
(ばねの弾性力をfとする)

\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・力には2種類ある
①接触力
…くっついている点や面ではたらく力→いろいろある
②非接触力
…くっついていなくてもはたらく力→重力\(mg\) など
3.問題3(作用・反作用の法則)
\(\underline{\bf{問題3}}\)
氷の上で静止している人が壁を押すと、人は壁から離れる向きに動いた。
このとき、人は何から力を受けて動いたか?
氷と人の間および、壁と人の間に摩擦力ははたらかないとする。
\(\underline{\bf{解答3}}\)
問題文から、人が壁を押したときに、人は図の右向き(壁から離れる向き)に動くことが分かります。
このとき、人にかかっている力を考えます。
非接触力である重力\(mg\)は常にはたらいており、鉛直下向きです。
次に接触力をみつけていきますが、人は氷と壁に接触しています。
このことから、氷と壁から垂直抗力を受けます。(問題文から摩擦力ははたらかない)
上記の重力と垂直抗力を図示すると下図のようになります。
(氷から受ける垂直抗力を\(N_{氷}\)、壁から受ける垂直抗力を\(N_{壁}\)とする)
上図から
\(\displaystyle{\begin{eqnarray}&&\bf{人は壁から\textcolor{red}{離れる向きに動く}}\\\Leftrightarrow&&\bf{右向きに力がはたらく(∵つりあっていたら動かない)}\\\Leftrightarrow&&\bf{右向きの力N_{壁}(壁から人への垂直抗力)}\end{eqnarray}}\)
よって、人は"壁から"力を受けて動いたことになります。
ここで、人は壁を押したことにより、壁は人から力を受けています。
それと同時に、作用・反作用の法則により、人も壁から力を受けます。
このことから、壁が人から受けた力の反作用で人は右向きに動いたことになります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
〇作用・反作用の法則
・接触面や接触点での力(逆向き、同じ大きさ、同一作用線)のペア
・重力や磁力でのペア(非接触力)
4.問題4(「つりあいの力」と「作用・反作用の力」の違い)
\(\underline{\bf{問題4}}\)
下図のように、水平面上に物体が静止しているとする。
このとき、物体と地球に注目し、物体にはたらいている力および、地球にはたらいている力を図示せよ。
また、図示した力のうち、「つりあいの力」の関係および、「作用・反作用」の関係にある力をそれぞれ答えよ。
\(\underline{\bf{解答4}}\)
今回は、着目する必要があるものが2つあります。(物体と地球)
このように、主人公が2つ以上あるとき(はたらいている力を考える物体が2つ以上あるとき)は\(\textcolor{green}{\bf{別々の図}}\)を描きます。
まずは物体について、いつものように力を描いていきます。
非接触力である重力\(mg\)は常にかかっており、地面と接しているので接触力である垂直抗力がかかっています。
左右方向には接触している部分はないので、力ははたらかず、静止していることから摩擦力もかかっていません。(摩擦力がかかっていれば、左右どちらかに力がかかり動いてしまう)
以上のことから、物体にかかっている力は、下図のようになります。
ここで重力について深掘りします。
詳しくは万有引力の項で学ぶことになりますが、「重力」とは地表付近における「万有引力」のこととなります。
また「万有引力」は、お互いに引き付ける方向にはたらきます。
上図の物体にはたらいている重力は、「地球」が「物体」を引き付ける力となります。
ここで注目したいのは、「万有引力(重力)」は「お互いに引き付ける力」という部分です。
よって、地球が物体を引き付けているのと同時に、物体が地球を引き付けてもいます。
以上のことをふまえて、地球にはたらいている力を考えてみます。
上述のように、物体と地球の間には「万有引力(重力)」がはたらいているので、地球の中心から物体の中心の向きに重力がはたらいています。
また、地球と物体は接しているので、この部分に垂直抗力が地球を貫く向きにはたらいています。
よって、地球にはたらいている力は下図のようになります。
比較整理すると、下図のようになります。
次に、「つりあいの力」と「作用・反作用の力」をみていきます。
つりあいの力
→「1つ」の物体に同一直線上にはたらき、同じ大きさで逆向き
作用・反作用の力
→「2つ」の物体に同一直線上にはたらき、同じ大きさで逆向き
以上のことを考えると、「つりあいの力」と「作用・反作用の力」の関係にある力は、それぞれ下図のようになります。
(力の文字の色は、比較整理した上図の色と対応しています。上図と比較しながら見てみてください)
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
〇つりあいの力
→同一の物体が受ける力
〇作用・反作用の力
→異なる2つの物体が及ぼしあう力
5.問題5(力の描き方見つけ方)
\(\underline{\bf{問題5}}\)
次の斜線で表された物体にかかっている力を、ベクトル(→)で図示せよ。
ただし、重力を\(mg\)、垂直抗力をN、張力をT、摩擦力をf、ばねの弾性力を\(f_s\)、浮力を\(f_f\)、外力をFとし、前述の記号をベクトルのそばに書き添えること。
また、同じ種類の力がかかっており、これらの力の大きさが異なる場合は\(N^{\prime}\)や\(N_1\)などで大きさが異なっていることが分かるようにせよ。(おなじ大きさならば、添え字などは必要ない)
\(\underline{\bf{解答5}}\)
解答は下図のようになります。
6.問題6(力の描き方見つけ方)
\(\underline{\bf{問題6}}\)
次の物体または人にはたらく力をベクトル(→)でそれぞれ描け。
その際、その力が重力の場合は\(mg\)、垂直抗力の場合N、摩擦力の場合f、張力の場合T、ばねの弾性力の場合\(f_s\)、浮力の場合\(f_f\)をベクトルの傍に書き添えること。
また、同じ種類の力がかかっており、これらの力の大きさが異なる場合は\(N^{\prime}\)や\(N_1\)などで大きさが異なっていることが分かるようにせよ。(おなじ大きさならば、添え字などは必要ない)
\(\underline{\bf{解答6}}\)
解答は下図のようになります。
特に、(7)と(8)について、下図の力のペアはそれぞれ作用・反作用の関係となります。
物体Bの摩擦力の向きは分かりやすいと思いますが、物体Aの摩擦力の向きを把握するのは難しいと思います。
このような場合には、まず物体Bの摩擦力を考えたあとに、物体Aには物体Bの反作用の力がはたらいていると考え、物体Bとは逆向きの摩擦力を考えると分かりやすいと思います。
7.問題7(力の描き方見つけ方)
\(\underline{\bf{問題7}}\)
次の物体または人にはたらく力をベクトル(→)でそれぞれ描け。
その際、その力が重力の場合は\(mg\)、垂直抗力の場合N、摩擦力の場合f、張力の場合T、ばねの弾性力の場合\(f_s\)、浮力の場合\(f_f\)をベクトルの傍に書き添えること。
また、同じ種類の力がかかっており、これらの力の大きさが異なる場合は\(N^{\prime}\)や\(N_1\)などで大きさが異なっていることが分かるようにせよ。(おなじ大きさならば、添え字などは必要ない)
ただし、空気抵抗は無視するものとする。
\(\underline{\bf{解答7}}\)
解答は下図のようになります。
8.問題8(力の描き方見つけ方)
\(\underline{\bf{問題8}}\)
次の物体または人にはたらく力をベクトル(→)でそれぞれ描け。
その際、その力が重力の場合は\(mg\)、垂直抗力の場合N、摩擦力の場合f、張力の場合T、ばねの弾性力の場合\(f_s\)、浮力の場合\(f_f\)をベクトルの傍に書き添えること。
また、同じ種類の力がかかっており、これらの力の大きさが異なる場合は\(N^{\prime}\)や\(N_1\)などで大きさが異なっていることが分かるようにせよ。(おなじ大きさならば、添え字などは必要ない)
ただし、空気抵抗は無視するものとする。
\(\underline{\bf{解答8}}\)
解答は下図のようになります。
(11)について、重力は下向き、垂直抗力は左斜め上向き(左向きと上向き)、ばねの弾性力は左斜め下向き(左向きと下向き)となっており、これらの力だけだと、右向きの力がないので左向きに動いてしまうことになります。
問題文の前提から、物体は静止しているので右向きの力が必要となります。
よって、コンベアと物体の間に摩擦力が必要であることがわかります。
はてなブログ内関連記事
6.力のはたらきとつりあい
この記事は力のつりあいの条件や、各種力についての解説記事になります。
力については、非接触力や接触力、物体にかかっている力の見つけ方についても述べていきます。
また、水圧ρdgや浮力ρVgの導き方についても解説しています。
作用反作用については、「つりあいの力」と「作用・反作用の力」の違いについても解説しています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.力のつりあい
物体が静止しているとき、物体にかかっている力は\(\textcolor{red}{\bf{つりあっています}}\)。
力が左右方向と上下方向にかかっている場合の、つりあいの条件は
①
物体にかかっている上向きの力の合力と下向きの力の合力の大きさが同じで、同一直線上にある。
②
物体にかかっている右向きの力の合力と左向きの力の合力の大きさが同じで、同一直線上にある。
となります。
(力の向きが逆で、大きさが同じ)
上記では、上下左右方向での条件でしたが、自分で\(x-y\)座標を定めた場合には、\(x\)軸方向と\(-x\)軸方向、\(y\)軸方向と\(-y\)軸方向の力の合力の大きさが同じという条件になります。
また、上記のことは物体にかかっている力のベクトルの合力が\(0\)であることを意味しています。
すなわち、物体にかかっている力が、\(F_1,F_2,F_3\cdots\)のとき、物体が静止している(つりあっている)なら
\(\displaystyle{\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots=\vec{0}}\)
となります。
\(F_1,F_2,F_3\cdots\)をそれぞれ\(x\)軸方向と\(y\)軸方向に分解して、成分で考えてみます。
(力の分解についてはこちら→力とベクトル)
それぞれの力の成分表示が
\(\displaystyle{\vec{F_1}=\left(\begin{eqnarray}&&F_{1x}\\&&F_{1y}\end{eqnarray}\right)}\)
\(\displaystyle{\vec{F_2}=\left(\begin{eqnarray}&&F_{2x}\\&&F_{2y}\end{eqnarray}\right)}\)
\(\displaystyle{\vec{F_3}=\left(\begin{eqnarray}&&F_{3x}\\&&F_{3y}\end{eqnarray}\right)}\)
\(\displaystyle{\vdots}\)
とすると、
\(\displaystyle{\begin{eqnarray}&&\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots=\vec{0}\\\\\Leftrightarrow&&{\left(\begin{array}{c}F_{1x}\\F_{1y}\end{array}\right)}+{\left(\begin{array}{c}F_{2x}\\F_{2y}\end{array}\right)}+{\left(\begin{array}{c}F_{3x}\\F_{3y}\end{array}\right)}+\cdots={\left(\begin{array}{c}0\\0\end{array}\right)}\end{eqnarray}}\)
となり、成分のみで考えると物体がつりあう際には
\(\displaystyle{F_{1x}+F_{2x}+F_{3x}+\cdots=0}\)
↑
\(x\)軸方向の合力が\(0\)(\(x\)軸方向のつりあい)
\(\displaystyle{F_{1y}+F_{2y}+F_{3y}+\cdots=0}\)
↑
\(y\)軸方向の合力が\(0\)(\(y\)軸方向のつりあい)
となります。
2.非接触力と接触力
力には\(\textcolor{green}{\bf{非接 触力}}\)と\(\textcolor{red}{\bf{接 触力}}\)があります。
\(\textcolor{green}{\bf{○非接 触力}}\)
物体同士が触れ合っていなくてもはたらく力。
\(\textcolor{red}{\bf{○接 触力}}\)
物体同士が触れ合ってはたらく力。
例として、代表的な力の種類と力の向きを載せておきます。
○重力(\(\textcolor{green}{\bf{非接 触力}}\))
向き:鉛直下向き
○張力(\(\textcolor{red}{\bf{接 触力}}\))
向き:糸が抜ける向き
○弾性力(\(\textcolor{red}{\bf{接 触力}}\))
向き:伸び、縮みと逆の方向(ばねが自然長に戻ろうとする方向)
○垂直抗力(\(\textcolor{red}{\bf{接 触力}}\))
向き:接触面、接触点と直角で、自分を貫く方向。
次から、上記に載せた代表的な力に加えて、様々な力について解説していきます。
3.重さと質量
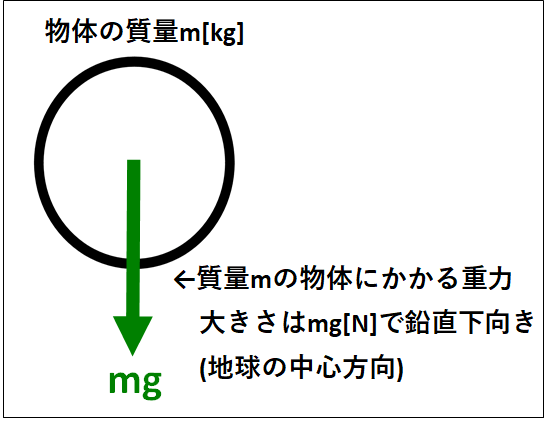
物体にはたらく重力の大きさを"物体の重さ"といいます。
重力の大きさは、
質量:\(m[kg]\)
重力加速度:\(g[m/s^2]\)
を用いて、
\(\textcolor{red}{\bf{mg[N]}}\)
と表されます。
(質量×重力加速度)
質量の\(m\)は\(mass\)(質量)の頭文字、重力加速度の\(g\)は\(gravitational acceleration\)(重力加速度)の頭文字となります。
重力の単位に用いられている"\(N\)"(ニュートン)は力の単位であり、質量と重力加速度を掛けると単位は
\(kg・m/s^2\)
となるので、\(kg・m/s^2\)の別の表し方となります。
(\(N=kg・m/s^2\))
この\(N\)は、\(kg・m/s^2\)からも分かる通り、\(1kg\)の物体に\(1m/s^2\)の加速度を生じさせる力の単位となります。
体重計などで表示される数値は、質量ではなく重さ(重力の大きさ)となります。
重力の向きは物体の中心から鉛直下向き(地球の中心方向)となり、\(\textcolor{green}{\bf{非接 触力}}\)で\(\textcolor{red}{\bf{物体に常にはたらきます}}\)。
※
質量とは、物体の状態の変わりにくさを表す量です。
↓
・静止している物体は、質量が大きいほど動かしにくい。
・運動している物体は、質量が大きいほど止めにくく、運動の方向も変えにくい。
4.張力
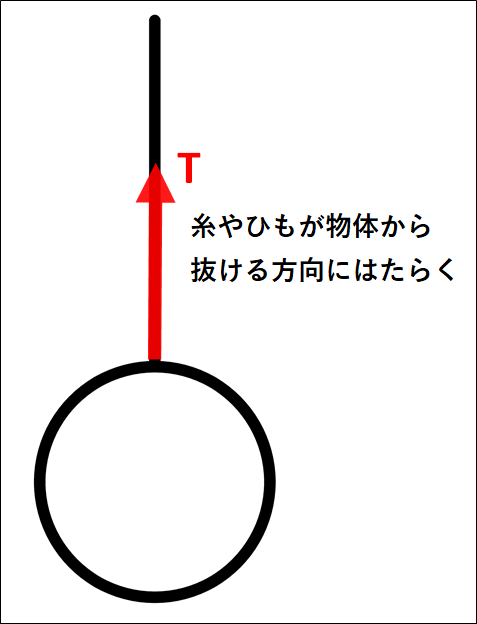
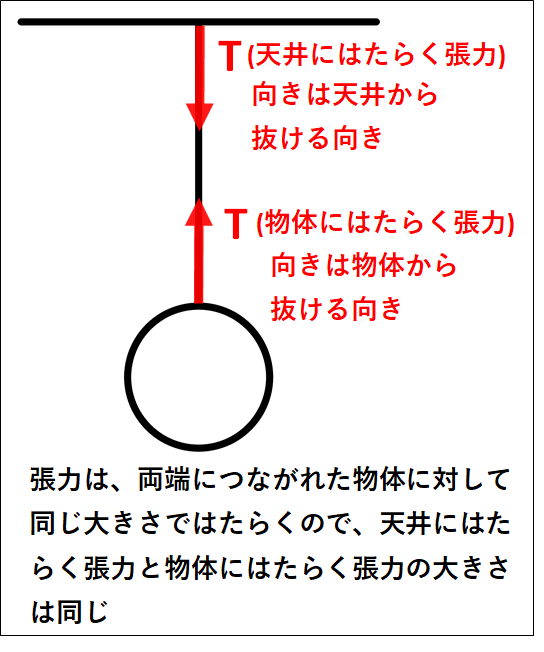
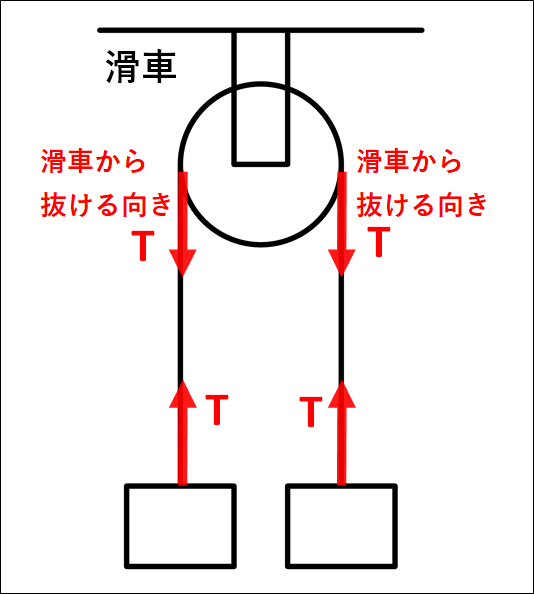
張力はたいてい文字"\(T\)"(\(tention\):張力 の頭文字)で表され、物体から糸やひもが抜ける方向にはたらきます。
また、張力は"糸やひもの両端につながれた物体に対して、同じ大きさ"ではたらきます。
張力も力なので、単位は\(N\)(ニュートン)で、\(\textcolor{red}{\bf{接 触力}}\)となります。
たいていの場合は問題文中に、"軽い糸"や"軽いひも"と記述されており、軽いというのは"質量を無視できる"ということです。
なので上記の記述があった際には、普通重力は常にはたらきますが、糸やひも自体の重力は考えなくてもよいです。
5.ばねの弾性力
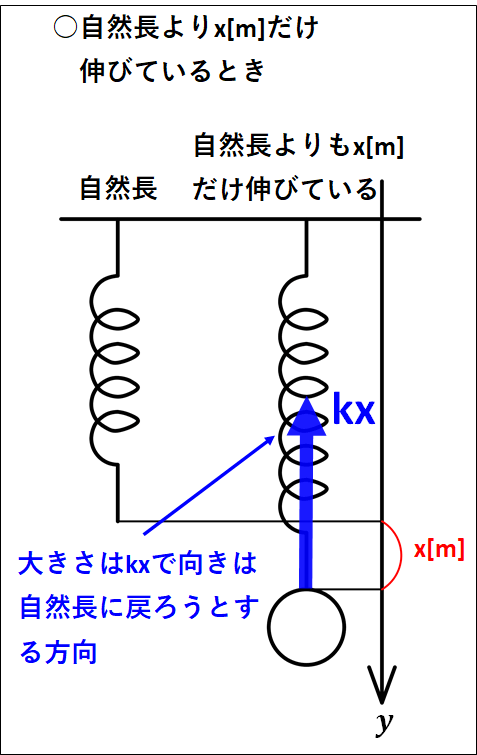
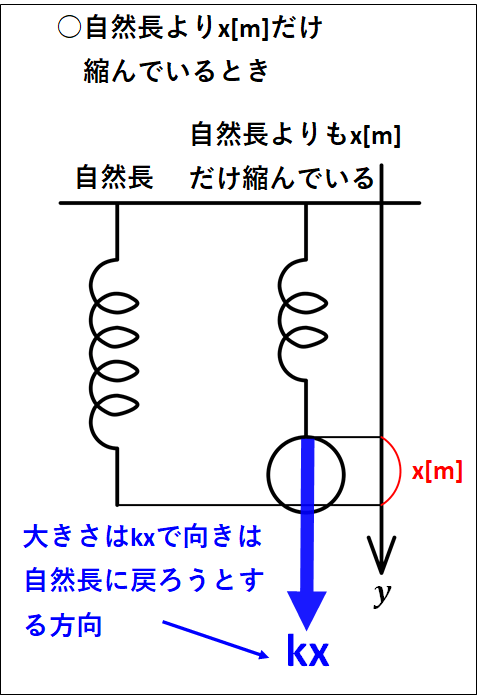
ばねに力が加わっていないときのばねの長さを"自然長"といい、ばねを自然長よりも伸ばしたり縮めたりしたときにばねは自然長に戻ろうとします。
このばねが自然長に戻ろうとする力をばねの"弾性力"といいます。
ばねの弾性力の向きは、自然長に戻ろうとする方向となります。
すなわち、ばねが伸びていれば縮む方向に、ばねが縮んでいれば伸びる方向が弾性力の向きとなります。
また、ばねの弾性力の大きさは、ばねの自然長からの伸びや縮みに比例します。
ばねの伸びまたは縮みを\(x[m]\)、比例定数を\(k[N/m]\)とするとばねの弾性力の大きさは
\(\displaystyle{kx[N]}\)
と表せます。
(比例定数×伸びor縮み)
単位は、比例定数と伸びまたは縮みを掛けているので\(N/m×m=N\)となります。
上記比例定数\(k\)を"ばね定数"といいます。
ばねの弾性力は\(\textcolor{red}{\bf{接 触力}}\)です。
6.水圧
\(\bf{\underline{○圧力について}}\)
圧力とは、流体中(気体や液体)の物体が、流体から面に対して垂直に受ける力のことです。
単位面積(\(1m^2\))あたりに受ける力(\(N\))であり、単位は\(N/m^2\)(ニュートン毎平方メートル)となります。
また、\(N/m^2\)を別の単位\(Pa\)(パスカル)で表すことが多いです。(\(Pa=N/m^2\))
圧力を\(P\)(\(pressure\):圧力 の頭文字)とすると、この圧力\(P\)は次式で表されます。
\(\displaystyle{P[P a]=\frac{F[N]}{S[m^2]}}\)
\(F[N]\)は面にかかっている力、\(S[m^2]\)は力がかかっている面積です。
上式は、圧力は力を面積で割ったものであることを表しています。
また、この式から力\(F[N]\)は圧力\(P\)と面積\(S\)で表すと
\(\displaystyle{F[N]=P[N/m^2]×S[m^2]}\)
であることが分かります。
(圧力の式の両辺に\(S[m^2]\)を掛けた。力=圧力×面積)
特に、地上における大気の圧力を大気圧といい、その大きさ\(P_0\)は約\(1.0×10^5Pa\)です。
この大気圧は、"大気の重さ"によって発生します。
\(\bf{\underline{○水圧}}\)
水圧とは、水中の物体が水から受ける圧力のことです。
水圧も、大気圧が大気の重さが原因で発生するのと同様に、"水の重さ"が原因で発生します。
ここから、水中の物体にはたらく圧力を考えていきます。
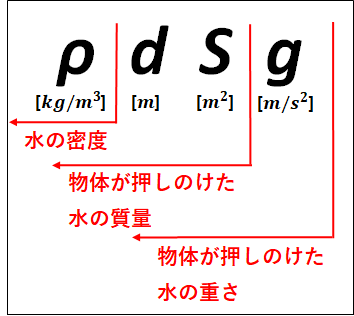
水の密度(単位体積(\(1m^3\))あたりの質量(\(kg\)))を\(ρ[kg/m^3]\)(\(ρ\)はローと読む)とし、水面から深さ\(d[m]\)の物体にはたらく圧力を考えます。
水中の物体の圧力を考えるにあたって、大気と水の角柱を考えて、この角柱の断面積を\(S[m^2]\)とします。
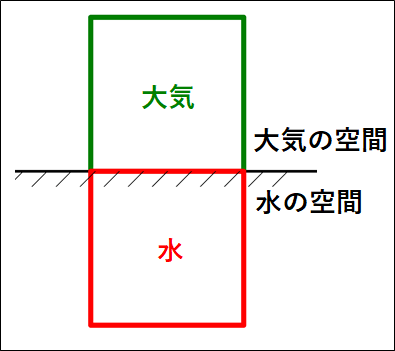
↓
大気と水を一体として考えます。
\(\textcolor{green}{m_{\bf{大}}}\)を大気の質量、\(\textcolor{red}{m_{\bf{水}}}\)を水の質量とします。
↓
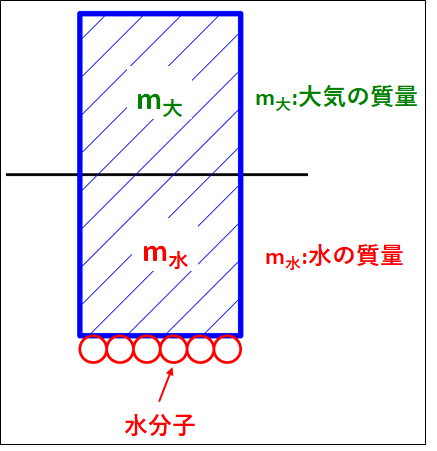
ここで、角柱の底面の水分子のつりあいについて考えます。
水分子の上には大気と水の重さ(重力)が下向きにかかっています。
水分子がつりあうためには、逆向きの力が加わっている必要があるので、これを上向きの力\(F\)(圧力による力)とします。
図示すると下図のようになります。
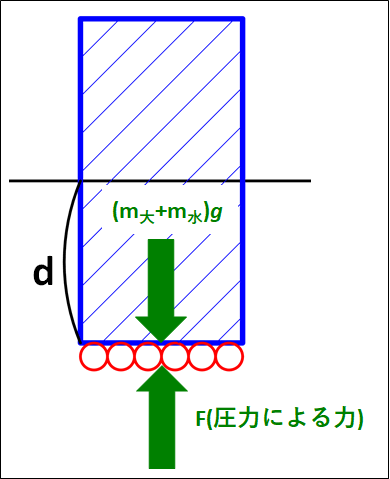
つりあうためには、上向きと力と下向きの力の大きさが等しければいいので、

上式において、力\(F\)は先ほど説明したように下から水分子にはたらく圧力を\(P\)とすると
\(\displaystyle{P=\frac{F}{S}}\)から\(F=P・S\)
大気圧は、大気の重さによって発生するので大気による重力は
\(m_{\bf{大}}g=P_0S\)
と、大気圧による力と同じものです。
また今、水の密度を\(ρ\)としているので、水の質量\(m_{\bf{水}}\)は\(Sdρ\)となります。
※
\(S[m^2]×d[m]\)で水部分の角柱の体積。
水の密度は\(ρ[kg/m^3]\)(単位体積あたりの質量)なので、これに体積を掛けると水の質量となる。
\(\displaystyle{\begin{eqnarray}&&S[m^2]×d[m]×ρ[kg/m^3]\\&=&Sd[m^3]×ρ[kg/m^3]\\\\&=&Sdρ[kg]\end{eqnarray}}\)

以上のことから、つりあいの式を変形していって

式の結果から、水圧は
\(\displaystyle{\textcolor{red}{ρdg}[N/m^2]}\)
で表され、水深(\(d[m]\))が深いほど大きくなることが分かります。
また、水面から深さ\(d[m]\)の物体にはたらく圧力\(P\)は
\(P=P_0+ρdg\)
で表されることが分かります。
7.浮力
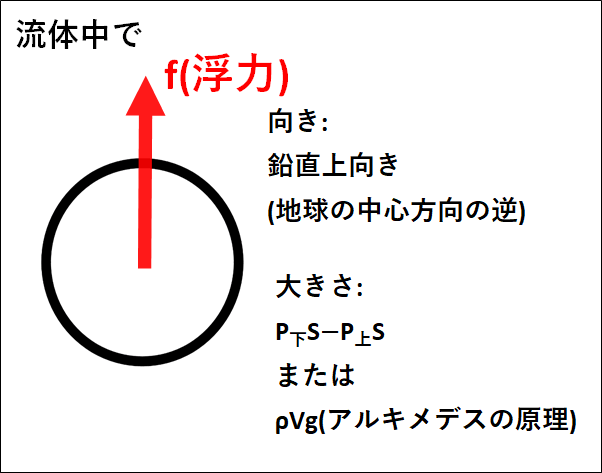
浮力とは、流体中の物体が流体から受ける力で、向きは"鉛直上向き"となります。
流体中の物体の、上面にかかる圧力と下面にかかる圧力の差によって発生します。
浮力がどのように表されるかについて考えていきます。
水の密度を\(ρ[kg/m^3]\)、物体を各面\(S[m^2]\)の立方体とし、下図のような状態を考えます。
(水圧は面に対して垂直にかかる)
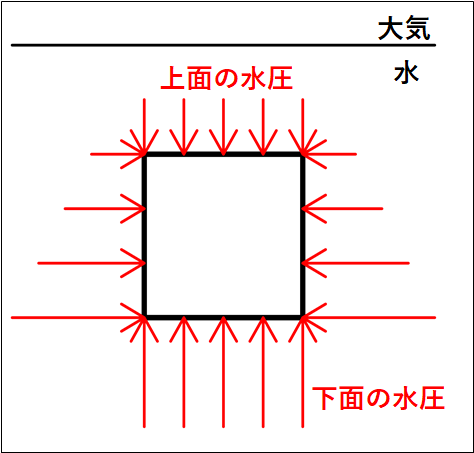
水圧は\(ρdg\)から深さが同じところでは同じ大きさとなります。
よって、左右方向の力はつりあうので、上下方向のみを考えます。
物体の上面にかかる水圧を\(P_{\bf{上}}\)、下面にかかる水圧を\(P_{\bf{下}}\)とすると、水圧による力はそれぞれ\(P_{\bf{上}}S\)、\(P_{\bf{下}}S\)となります。
水面から物体の上面までの距離を\(h[m]\)、物体の高さを\(d[m]\)とすると、下図のようになります。
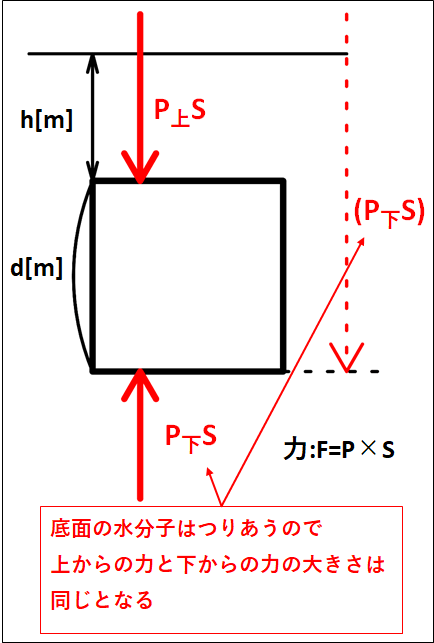
図から水圧は深い方が大きくなるので\(P_{\bf{上}}S{\lt}P_{\bf{下}}S\)。
よって、浮力の大きさを\(f\)とすると\(f=P_{\bf{下}}S-P_{\bf{上}}S\)となります。
(浮力は、上面と下面の水圧による力の差。上面にかかる力より下面にかかる力の方が大きいので、浮力は鉛直上向き)
また、水圧の部分で述べたように、水圧は\(\displaystyle{\textcolor{red}{ρdg}[N/m^2]}\)で表されます。
\(d\)は深さを表しますが、物体の上面までの深さは\(h[m]\)、下面までの深さは\( (h+d)[m]\)です。
実際に浮力\(f\)を計算してみると
\(\displaystyle{\begin{eqnarray}f&=&P_{\bf{下}}S-P_{\bf{上}}S\\\\&=&{P_0+ρ(h+d)g}S-{P_0+ρhg}S\\\\&=&P_0S+ρ(h+d)Sg-(P_0S+ρhSg)\\\\&=&P_0S+ρhSg+ρdSg-(P_0S+ρhSg)\\\\&=&ρdSg\end{eqnarray}}\)
よって、浮力\(f\)は
\(f=ρdSg[N]\)
で表されます。
この\(ρdSg\)の意味は以下のようなものになります。
また、上式の\(dS\)は物体の体積を表しているので、これを体積\(V\)で書きなおすと、
\(ρdSg=ρVg\)
となります。
単位をみてみると、
\(kg/m^3×m^3×m/s^2=kg・m/s^2=N\)
と、力の単位となっています。

上記の式を"アルキメデスの原理"といい、流体中の物体にはたらく浮力は、その物体が押しの出た流体の重さに等しいことを表しています。
問題を解く上で、
浮力:\(P_{\bf{下}}S-P_{\bf{上}}S\)
アルキメデスの原理:\(ρVg\)
のどちらの式を使うのかについてですが、問題文中に大気圧\(P_0\)があらわれたのなら、\(P_{\bf{下}}S-P_{\bf{上}}S\)を用います。
(アルキメデスの原理に\(P_0\)は現れないから)
下記に、浮力の向きと大きさを図示しておきます。
8.抗力
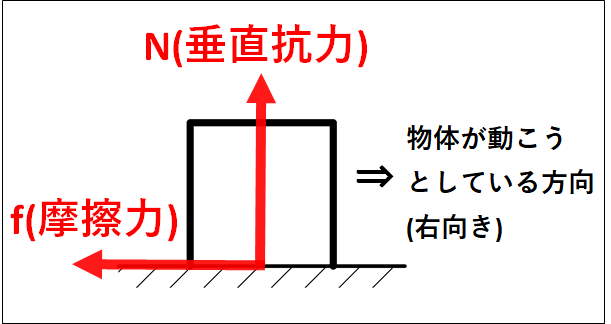
抗力とは、物体が接触面や接触点から受ける力のことです。
特に、面に垂直な成分を\(\textcolor{red}{\bf{垂直抗力}}\)、面に平行な成分を\(\textcolor{red}{\bf{摩擦力}}\)といいます。
抗力は、\(\textcolor{red}{\bf{接 触力}}\)です。
垂直抗力\(N\):
接触面や接触点に垂直で、自分を貫く方向にはたらく。
摩擦力\(f\):
接触面や接触点に平行で、物体が動こうとする向きと逆向きにはたらく。
摩擦力については、次で詳しく解説します。
9.摩擦力
摩擦力には、\(\textcolor{red}{\bf{静止摩擦力}}\)と\(\textcolor{red}{\bf{動摩擦力}}\)があります。
摩擦力がはたらいていても、物体が静止しているときには静止摩擦力が、物体が動いているときには動摩擦力がはたらきます。
この2つの摩擦力について説明していきます。
\(\bf{\underline{○静止摩擦力}}\)
"粗い面上"の物体にかかり、物体が動こうとする向きと逆向きにかかります。
粗い面上の物体に力を加えても、小さい力では物体は動きません。
これは、物体が動こうとする向きと逆向きに静止摩擦力がかかるからです。
物体に加える力を大きくしていくと、静止摩擦力も大きくなっていき、物体が動き出す直前で最大となります。
物体が"静止"しているときの摩擦力を"\(\textcolor{red}{\bf{静止摩擦力}}\)"といい、動き出す直前の摩擦力を"\(\textcolor{red}{\bf{最大静止摩擦力(最大摩擦力)}}\)"といいます。
実験から、最大静止摩擦力\(f_0[N]\)は、物体にはたらく垂直抗力の大きさ\(N[N]\)に比例し、
\(f_0=μN\)
と表されることがわかっています。
\(μ\)はミューと読み、この比例定数を"\(\textcolor{red}{\bf{静止摩擦係数}}\)"といいます。
\(\bf{\underline{○動摩擦力}}\)
"\(\textcolor{red}{\bf{動摩擦力}}\)"は粗い面上で、物体が"動いているとき"にはたらく摩擦力になります。
実験から、動摩擦力\(f^{\prime}[N]\)は垂直抗力の大きさ\(N[N]\)に比例し、
\(f^{\prime}=μ^{\prime}N\)
と表されることがわかっています。
上記の比例定数\(μ^{\prime}\)を"\(\textcolor{red}{\bf{動摩擦係数}}\)"といいます。
静止摩擦力は、力を加えていくと大きくなっていきますが、最大静止摩擦力を越えて物体が動き出すと、このときの動摩擦力は"一定の値"となります。
\(\bf{\underline{○摩擦力と力のグラフ}}\)
摩擦力(静止摩擦力と動摩擦力)と物体に加えた力\(F\)の関係を表したグラフを載せておきます。
物体に加えた力が大きくなっていくと、静止摩擦力も大きくなってく様子や、最大静止摩擦力を超えると物体が動き出し、動摩擦力がはたらく様子を観察してください。
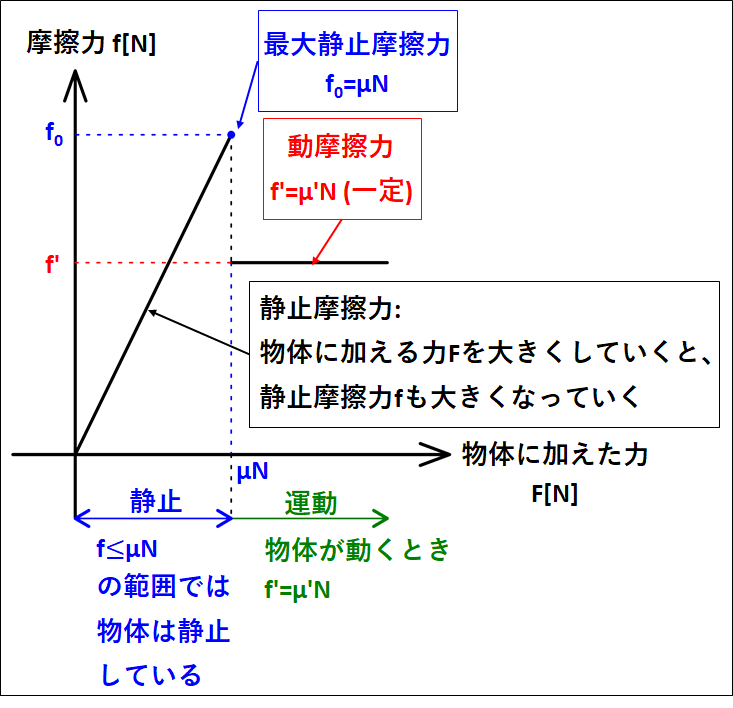
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\begin{eqnarray}&&{\bf{物体は静止する}}\\\Leftrightarrow&&f{\le}μN (静止摩擦力)\\\\&&μ:{\bf{静止摩擦係数}}\end{eqnarray}}\)
\(\textcolor{red}{\begin{eqnarray}&&{\bf{物体は動いている}}\\\Leftrightarrow&&f^{\prime}=μ^{\prime}N (動摩擦力)\\\\&&μ^{\prime}:{\bf{動摩擦係数}}\end{eqnarray}}\)
また、一般に
\(μ^{\prime}{\lt}μ\)
(動摩擦係数<静止摩擦係数)
10.物体にかかっている力の見つけ方
物体にかかっている\(\textcolor{red}{\bf{接 触力}}\)をみつけるには、注目している物体の表面をなでまわすと良いです。
なでまわしたときに、当たる部分があるのでそこに何らかの力がかかっています。
(あたる部分がなければ、接触力ははたらいていない)
\(\textcolor{green}{\bf{非接 触力}}\)
→重力は、必ず物体にはたらく
\(\textcolor{red}{\bf{接 触力}}\)
→物体の表面をなでまわしたときに当たる、面や点にはたらく
例として、次のような状況について考えていきます。
例)
質量\(m\)の物体\(A\)の左側にばねが取り付けられ、右側に軽いひもがつけられている。
この物体\(A\)が右向きに引っ張られて、ばねが自然長から\(x\)だけ伸びており、この状態で静止している。
床はなめらかで、ばね定数を\(k\)、重力加速度を\(g\)とする。
まず、非接触力について考えます。
物体\(A\)には非接触力である重力がはたらいています。
物体\(A\)の質量は\(m\)なので、重力の大きさは\(mg\)(質量×重力加速度)で、鉛直下向きにはたらきます。
次に、接触力について考えていきます。
先ほど述べたように、物体の表面をなでまわしてみます。
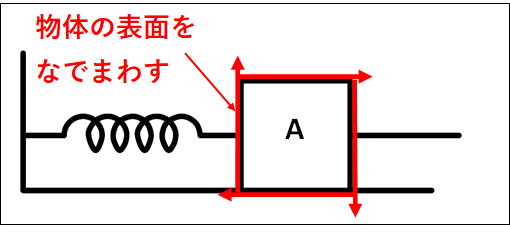
そうすると、なでまわしている最中にあたる部分があることがわかると思います。
この部分に接触力がはたらいています。
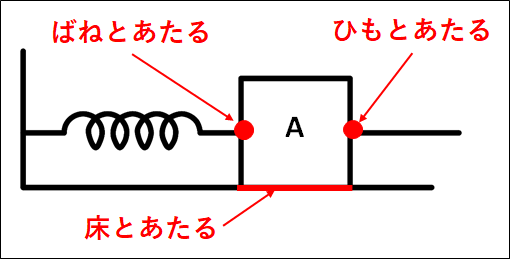
これで、接触力がはたらいている部分はわかりました。
次に、接触力の種類について考えていきます。
\(\bf{\underline{○ばねとあたっている部分}}\)
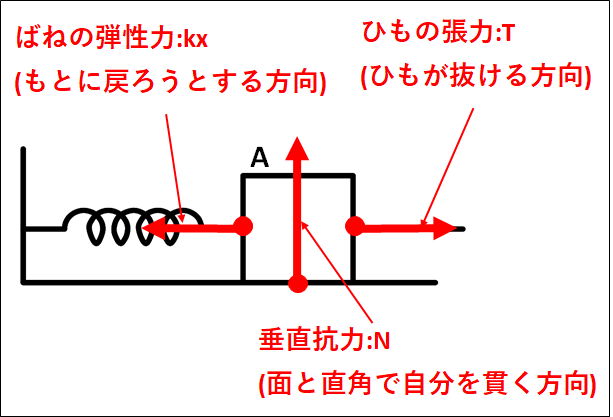
この部分は、ばねとあたっているので"ばねの弾性力"がはたらいています。
いま、物体は右向きに引っ張られており、ばねは\(x\)だけ伸びているので、この弾性力の大きさは\(kx\)となります。
向きは、ばねが右向きに伸びているので、自然長に戻ろうとする左向きとなります。
\(\bf{\underline{○ひもとあたっている部分}}\)
この部分はひもとあたっているので張力となります。
この張力を\(T\)としておきます。
向きは、ひもが抜ける方向なので、右向きとなります。
\(\bf{\underline{○床とあたっている部分}}\)
この部分には抗力がはたらいていますが、床はなめらかなので摩擦力ははたらいておらず、垂直抗力のみがはたらいています。
(摩擦力は粗い面ではたらく。なめらかな面でははたらかない)
この垂直抗力を\(N\)としておきます。
向きは、面と垂直で自分(物体\(A\))を貫く方向になるので、鉛直上向きとなります。
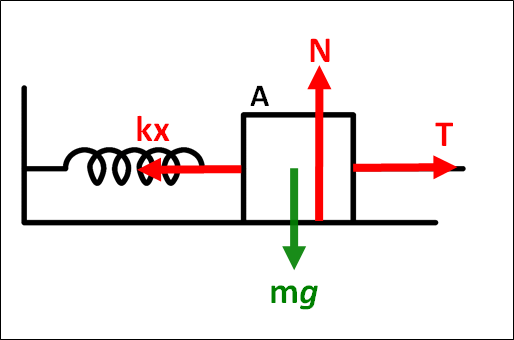
以上を図示すると、下図のようになります。
物体\(A\)にかかっているすべての力を図示すると、以下のようになります。
ついでに、物体は静止しているのでつりあいの条件も確認しておきます。
物体が静止する(つりあう)条件は、上向きの力と下向きの力の大きさが等しい、右向きの力と左向きの力の大きさが等しい、なので
\(\displaystyle{\left\{\begin{eqnarray}&&{\bf{(上向きの力)}}={\bf{(下向きの力)}}\\&&{\bf{(右向きの力)}}={\bf{(左向きの力)}}\end{eqnarray}\right.}\)
となります。
今、図示した力から
上向きの力→垂直抗力:\(N\)
下向きの力→重力:\(mg\)
右向きの力→張力:\(T\)
左向きの力→弾性力:\(kx\)
なので、物体が静止する条件(つりあいの条件)は以下のようになります。

また、つりあいの条件を立てることで、静止しているときの物体にはたらく未知の力の大きさがわかります。
上記の例でいうと、ひもの張力\(T\)と垂直抗力\(N\)の力の大きさは分かりませんでしたが、つりあいの条件を立式したことでそれぞれ\(mg\)と\(kx\)であることがわかりました。
11.作用・反作用の法則
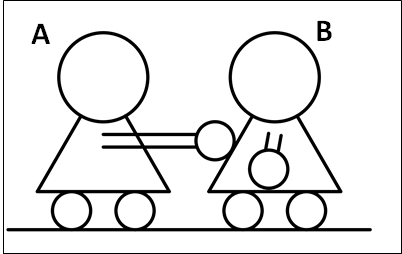
\(A\)さんが\(B\)さんを手で押すときを考えてみます。
\(A\)さんに注目すると、\(A\)さんの手は\(B\)さんにあたっているので\(A\)さんは\(B\)さんから垂直抗力を受けます。
逆に\(B\)さんに注目すると、\(B\)さんは\(A\)さんに手をあてられているので、\(B\)さんは\(A\)さんから垂直抗力を受けます。
それぞれの垂直抗力は、自分を貫く方向となるので、\(A\)さんにはたらいている垂直抗力と\(B\)さんにはたらいている垂直抗力の向きは逆向きとなります。
しかし、与えているまたは、与えられている力の大きさは同じなので、この2つの垂直抗力の大きさは同じになります。
このような同じ大きさで逆向き、また同一直線上にある、お互いに及ぼしあっている力の一方を作用、もう一方を反作用といいます。
一般的に、2つの物体が互いに力を及ぼし合うとき、作用と反作用は同一直線上にあり、逆向きで大きさが等しくなります。
これを、"\(\textcolor{red}{\bf{作用・反作用の法則}}\)"といいます。
(逆向き、同じ大きさ、同一直線上の力のペア)
また、"作用・反作用の法則"を"運動の第三法則"ともいいます。
上記に関して、実際に力を図示してみます。
例として、なめらかな床の上(氷など)で、静止している\(A\)が静止している\(B\)を押すことを考えます。
状況を図示すると以下のようになります。
次に、\(A\)、\(B\)それぞれについて注目して、かかっている力を考えていきます。
\(\bf{\underline{○Aについて}}\)
\(A\)に注目します。
まず、非接触力である重力が鉛直下向きにかかっているので、これを\(m_Ag\)とします。
次に、床から垂直抗力を受けます。
向きは、床と垂直で自分を貫く方向なので鉛直上向きにはたらきます。
この垂直抗力を\(N_A\)とします。
最後に、\(A\)は\(B\)を押しているので、この接触点で垂直抗力がはたらいています。
この垂直抗力を\(N\)とすると、\(N\)は自分を貫く方向である左向きにはたらきます。
これらすべての力を図示すると、下図のようになります。
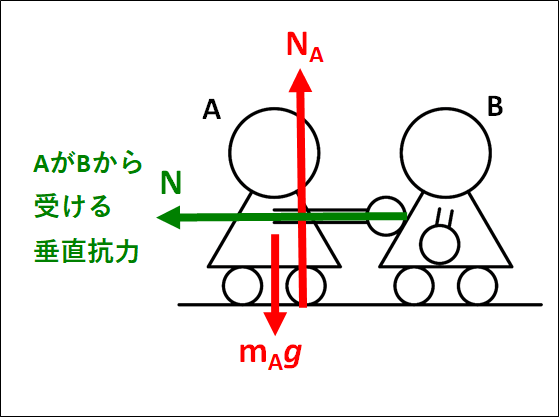
床からの垂直抗力\(N_A\)は、\(A\)をなでまわすと足が2点で接していますが、各足にはたらく垂直抗力の合力を\(N_A\)としています。
\(\bf{\underline{○Bについて}}\)
次に\(B\)に注目します。
まず、非接触力である重力が鉛直下向きにかかっているので、これを\(m_Bg\)とします。
次に、床から垂直抗力を受けます。
向きは、床と垂直で自分を貫く方向なので鉛直上向きにはたらきます。
この垂直抗力を\(N_B\)とします。
最後に、\(B\)は\(A\)に押されているので、この接触点で垂直抗力がはたらいています。
この垂直抗力を\(N\)とすると、\(N\)は自分を貫く方向である右向きにはたらきます。
これらすべての力を図示すると、下図のようになります。
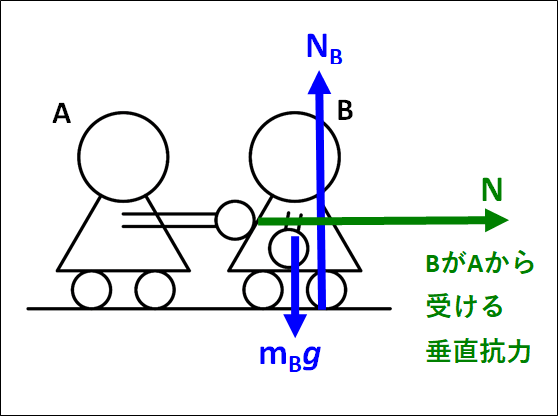
床からの垂直抗力\(N_B\)は、\(B\)をなでまわすと足が2点で接していますが、各足にはたらく垂直抗力の合力を\(N_B\)としています。
上の\(A\)に注目した場合にかかっている力と、\(B\)に注目した場合にかかっている力を見比べてみると、垂直抗力\(N\)は\(B\)が\(A\)から受けている力であると同時に、\(A\)が\(B\)から受けている力でもあります。
なので、この\(A\)が受けている垂直抗力と\(B\)が受けている垂直抗力は"作用・反作用"の関係となっています。
(逆向き、同じ大きさ、同一直線上のペア)
※
\(A\)について、上下方向では垂直抗力\(N_A\)と重力\(m_Ag\)がつりあいますが(上下方向には動かない)、左右方向については、左向きの垂直抗力\(N\)に対して、右向きの力がありません。
また\(B\)について、上下方向では垂直抗力\(N_B\)と重力\(m_Bg\)がつりあいますが(上下方向には動かない)、左右方向については、右向きの垂直抗力\(N\)に対して、左向きの力がありません。
なので、\(A\)と\(B\)は上下方向には動かないですが、左右方向には動きます。
はじめは\(A\)と\(B\)はともに静止しているので、\(A\)が\(B\)を押すと、\(A\)は垂直抗力\(N\)がはたらく左方向へ、\(B\)は垂直抗力\(N\)がはたらく右方向へそれぞれ動きます。
\(A\)が\(B\)を押した場合でも、なめらかな床の上では両者とも逆方向へと動くのは作用・反作用の力がはたらいているからということになります。
また、作用・反作用の法則は"接触力だけでなく、非接触力についても成り立ちます"。
作用・反作用例)
接触力の例:
\(A\)が床から受ける垂直抗力について
\(A\)は床から垂直抗力\(N_A\)を受けているが、床に注目すると、床も\(A\)から垂直抗力\(N_A\)を受けている。
\(A\)が受ける垂直抗力は鉛直上向き
床が受ける垂直抗力は、床を貫く方向である鉛直下向き
この\(A\)が床から受ける垂直抗力と、床が\(A\)から受ける垂直抗力は作用・反作用の関係にあります。
(逆向き、同じ大きさ、同一直線上のペア)
非接触力の例:
\(A\)が受ける重力について
\(A\)は地球の中心方向に引っ張られる重力\(m_Ag\)を受けているが、地球に注目すると、地球も\(A\)に引っ張られる重力\(m_Ag\)を受けている。(2つの物体がお互いに引き付けあう力を万有引力という)
\(A\)が地球から受ける重力は
\(A\)の中心→地球の中心
に向かう向き。
地球が\(A\)から受ける重力は
地球の中心→\(A\)の中心
に向かう向き。
この\(A\)が地球から受ける重力と、地球が\(A\)から受ける重力は作用・反作用の関係にあります。
(逆向き、同じ大きさ、同一直線上のペア)
また、「つりあいの力」と「作用・反作用の力」について、間違うこともあるので、この2つの違いについて述べておきます。
つりあいの力
→同一の物体が受ける力
作用・反作用の力
→"異なる2つの物体"が及ぼしあう力
となります。
はてなブログ内関連記事
5-1.力とベクトル(補足解説と練習問題)
力とベクトルの記事で解説した内容の練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、力とベクトルの記事で解説していなかった補足内容があれば、この記事に載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
本記事の関連記事はこちらになります。
目次
1.力の合成
1-1.問題1
\(\underline{\bf{問題1}}\)
次の力\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)の合成ベクトルを図示せよ。
\(\underline{\bf{解答1}}\)
ベクトルに関する知識を用いますので、こちらも参考にしてください。
→ベクトルの演算と成分表示
求めるベクトルは\(\overrightarrow{F_1}+\overrightarrow{F_2}\)なので、始点を決めて、この始点から\(\overrightarrow{F_1}\)進んでさらに\(\overrightarrow{F_2}\)だけ進んだ点を終点とするベクトルが求めるベクトルになります。
見やすくするためにベクトルをずらしていますが、\(\overrightarrow{F_1}\)の始点を求めるベクトルの始点として、\(\overrightarrow{F_1}\)の終点に\(\overrightarrow{F_2}\)の始点を平行移動します。
この\(\overrightarrow{F_1}\)の始点と\(\overrightarrow{F_2}\)の終点を結んだ下図の赤色のベクトルが求める\(\overrightarrow{F_1}+\overrightarrow{F_2}\)となります。
※座標で考えると
下図のようにx-y座標を設定し、1マス分を1Nとします。
(N(ニュートン)は力の単位)
\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)をそれぞれ成分表示すると
\(\displaystyle{\overrightarrow{F_1}=\left(\begin{array}{r}0\\+3\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_2}=\left(\begin{array}{r}0\\-2\end{array}\right)}\)
よって求めるベクトル\(\overrightarrow{F_1}+\overrightarrow{F_2}\)は成分同士を計算して
\(\displaystyle{\begin{eqnarray}\overrightarrow{F_1}+\overrightarrow{F_2}&=&\left(\begin{array}{r}0\\+3\end{array}\right)+\left(\begin{array}{r}0\\-2\end{array}\right)\\\\&=&\left(\begin{array}{r}0+0\\+3-2\end{array}\right)\\\\&=&\left(\begin{array}{r}0\\+1\end{array}\right)\end{eqnarray}}\)
これより、求めるベクトルは、設定した原点からx軸方向に0、y軸方向に+1だけ進んだ、先ほどの解答の赤色のベクトルとなります。
1-2.問題2
\(\underline{\bf{問題2}}\)
次の力\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)の合成ベクトルを図示せよ。
\(\underline{\bf{解答2}}\)
問題1のときと同様にして、始点を決めて、\(\overrightarrow{F_1}\)だけ進んだとことから\(\overrightarrow{F_2}\)だけ進んだ部分を終点とするベクトルを求めればよいです。
そのために\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)を平行移動してできる平行四辺形をつくります。
始点とした部分と、作成した平行四辺形の対角点を結んだベクトルが求めるベクトルである\(\overrightarrow{F_1}+\overrightarrow{F_2}\)となります。
よって、下図の赤色のベクトルが求めるベクトルとなります。
上図をみてみると、始点から右側に進むルートでは、\(\overrightarrow{F_1}\)だけ進んでから平行移動した\(\overrightarrow{F_2}\)だけ進んでいることがわかります。
また、始点から左下側に進むルートでは、\(\overrightarrow{F_2}\)だけ進んでから平行移動した\(\overrightarrow{F_1}\)だけ進んでいることがわかります。
これより、どちらのルートで進んでも\(\overrightarrow{F_1}+\overrightarrow{F_2}\)を求めていることになります。
※座標で考えると
下図のようにx-y座標を設定し、1マス分を1Nとします。
(N(ニュートン)は力の単位)
\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)をそれぞれ成分表示すると
\(\displaystyle{\overrightarrow{F_1}=\left(\begin{array}{r}+2\\0\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_2}=\left(\begin{array}{r}-1\\-3\end{array}\right)}\)
よって求めるベクトル\(\overrightarrow{F_1}+\overrightarrow{F_2}\)は成分同士を計算して
\(\displaystyle{\begin{eqnarray}\overrightarrow{F_1}+\overrightarrow{F_2}&=&\left(\begin{array}{r}+2\\0\end{array}\right)+\left(\begin{array}{r}-1\\-3\end{array}\right)\\\\&=&\left(\begin{array}{r}+2-1\\0-3\end{array}\right)\\\\&=&\left(\begin{array}{r}+1\\-3\end{array}\right)\end{eqnarray}}\)
これより、求めるベクトルは、設定した原点からx軸方向に+1、y軸方向に-3だけ進んだ、先ほどの解答の赤色のベクトルとなります。
1-3.問題3
\(\underline{\bf{問題3}}\)
次の力\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)の合成ベクトルを図示せよ。
\(\underline{\bf{解答3}}\)
問題2と同様にして、\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)を平行移動してできる平行四辺形の対角点と始点を結んだベクトルが求めるベクトルとなります。
よって、下図の赤色のベクトルが求めるベクトルです。
※座標で考えると
下図のようにx-y座標を設定し、1マス分を1Nとします。
(N(ニュートン)は力の単位)
\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)をそれぞれ成分表示すると
\(\displaystyle{\overrightarrow{F_1}=\left(\begin{array}{r}-1\\+3\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_2}=\left(\begin{array}{r}+3\\-2\end{array}\right)}\)
よって求めるベクトル\(\overrightarrow{F_1}+\overrightarrow{F_2}\)は成分同士を計算して
\(\displaystyle{\begin{eqnarray}\overrightarrow{F_1}+\overrightarrow{F_2}&=&\left(\begin{array}{c}-1\\+3\end{array}\right)+\left(\begin{array}{r}+3\\-2\end{array}\right)\\\\&=&\left(\begin{array}{r}-1+3\\+3-2\end{array}\right)\\\\&=&\left(\begin{array}{r}+2\\+1\end{array}\right)\end{eqnarray}}\)
これより、求めるベクトルは、設定した原点からx軸方向に+2、y軸方向に+1だけ進んだ、先ほどの解答の赤色のベクトルとなります。
1-4.問題4
\(\underline{\bf{問題4}}\)
次の力\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)の合成ベクトルを図示せよ。
\(\underline{\bf{解答4}}\)
問題2と同様にして、\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)を平行移動してできる平行四辺形の対角点と始点を結んだベクトルが求めるベクトルとなります。
よって、下図の赤色のベクトルが求めるベクトルです。
※座標で考えると
下図のようにx-y座標を設定し、1マス分を1Nとします。
(N(ニュートン)は力の単位)
\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)をそれぞれ成分表示すると
\(\displaystyle{\overrightarrow{F_1}=\left(\begin{array}{r}-3\\+0\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_2}=\left(\begin{array}{r}+1\\-3\end{array}\right)}\)
よって求めるベクトル\(\overrightarrow{F_1}+\overrightarrow{F_2}\)は成分同士を計算して
\(\displaystyle{\begin{eqnarray}\overrightarrow{F_1}+\overrightarrow{F_2}&=&\left(\begin{array}{r}-3\\0\end{array}\right)+\left(\begin{array}{r}+1\\-3\end{array}\right)\\\\&=&\left(\begin{array}{r}-3+1\\+0-3\end{array}\right)\\\\&=&\left(\begin{array}{r}-2\\-3\end{array}\right)\end{eqnarray}}\)
これより、求めるベクトルは、設定した原点からx軸方向に-2、y軸方向に-3だけ進んだ、先ほどの解答の赤色のベクトルとなります。
1-5.問題5
\(\underline{\bf{問題5}}\)
次の力\(\overrightarrow{F_1}\)、\(\overrightarrow{F_2}\)および\(\overrightarrow{F_3}\)の合成ベクトルを図示せよ。
\(\underline{\bf{解答5}}\)
今回求めるベクトルは、3つのベクトルの合成ベクトルとなります。
すなわち
\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}}\)
を求めることになります。
前の問題を解く際に、2力の合力はそれぞれのベクトルを平行移動してできる平行四辺形から求めることができました。
なので、今回も2力ずつ合成していき合成ベクトルを求めていきます。
つまり
\(\displaystyle{(\overrightarrow{F_1}+\overrightarrow{F_2})+\overrightarrow{F_3}}\)
と考えます。
はじめに、\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}}\)を求めていきます。
前問と同様にして\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)を平行移動してできる平行四辺形を用いて、\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}}\)を求めると下図のようになります。
次に、求めた\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}}\)と\(\overrightarrow{F_3}\)の合成ベクトルを求めます。
こちらも同様にして、\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}}\)と\(\overrightarrow{F_3}\)を平行移動してできる平行四辺形を用いて求めると下図のようになります。
\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}}\)と\(\overrightarrow{F_3}\)の合成ベクトルを求めたことで、
\(\displaystyle{\begin{eqnarray}&&(\overrightarrow{F_1}+\overrightarrow{F_2})+\overrightarrow{F_3}\\\\&&=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\end{eqnarray}}\)
となり、求めるベクトルである\(\displaystyle{\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}}\)を求めたことになります。
よって、上図の赤色のベクトルが求めるベクトルとなります。
※座標で考えると
下図のようにx-y座標を設定し、1マス分を1Nとします。
(N(ニュートン)は力の単位)
\(\overrightarrow{F_1}\)、\(\overrightarrow{F_2}\)および\(\overrightarrow{F_3}\)をそれぞれ成分表示すると
\(\displaystyle{\overrightarrow{F_1}=\left(\begin{array}{r}-1\\-3\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_2}=\left(\begin{array}{r}-2\\+3\end{array}\right)}\)
\(\displaystyle{\overrightarrow{F_3}=\left(\begin{array}{r}+2\\+2\end{array}\right)}\)
よって求めるベクトル\(\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\)は成分同士を計算して
\(\displaystyle{\begin{eqnarray}\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}&=&\left(\begin{array}{r}-1\\-3\end{array}\right)+\left(\begin{array}{r}-2\\+3\end{array}\right)+\left(\begin{array}{r}+2\\+2\end{array}\right)\\\\&=&\left(\begin{array}{r}-1-2+2\\-3+3+2\end{array}\right)\\\\&=&\left(\begin{array}{r}-1\\+2\end{array}\right)\end{eqnarray}}\)
これより、求めるベクトルは、設定した原点からx軸方向に-1、y軸方向に+2だけ進んだ、先ほどの解答の赤色のベクトルとなります。
2.力の分解
2-1.問題1
\(\underline{\bf{問題1}}\)
下図の力をx軸方向のベクトル\(\vec{F}_x\)とy軸方向のベクトル\(\vec{F}_y\)に分解し図示せよ。
また、\(\vec{F}\)をx成分とy成分で表示せよ。
ただし、図中の\(\vec{F}\)の大きさは
\(|\vec{F}|=4N\)
とする。
(N(ニュートン)は力の単位)
\(\underline{\bf{解答1}}\)
ベクトルに関する知識と、三角関数に関する知識を用いますので、こちらも参考にしてください。
力の分解は、力の合成の逆の操作となります。
分解したいベクトルを対角辺とする平行四辺形を作図して、任意の(好きな)2方向のベクトルに分解することができます。
今回は、x軸方向とy軸方向に分解するので、このx軸とy軸に平行な辺で構成され、分解するベクトルを対角辺とする四角形を作図します。
次に、分解するベクトルの始点から、作図した四角形の辺上を通り、分解するベクトルの終点方向にそれぞれベクトルを作図します。
このベクトルは、x軸の向きとy軸の向きそれぞれで作図できます。
作図したベクトルは下図の赤色のベクトルとなり、これらがそれぞれもとのベクトルをx軸方向とy軸方向に分解したものとなります。
上図において、
\(\displaystyle{\vec{F}=\vec{F}_x+\vec{F}_y}\)
となっていることを確認してみてください。
次に、これらの成分を数値でみていきます。
三角関数から、x成分の大きさ\(|\vec{F}_x|\)は
\(\displaystyle{\begin{eqnarray}|\vec{F}_x|&=&|\vec{F}|\cos30°\\\\&=&4N×\frac{\sqrt{3}}{2}\\\\&=&2\sqrt{3}N\end{eqnarray}}\)
三角関数から、y成分の大きさ\(|\vec{F}_y|\)は
\(\displaystyle{\begin{eqnarray}|\vec{F}_y|&=&|\vec{F}|\sin30°\\\\&=&4N×\frac{1}{2}\\\\&=&2N\end{eqnarray}}\)
また、ベクトルは向きと大きさをもつので、大きさだけでなく向きも考えなけらばなりません。
\(\vec{F}_x\)はx軸の正の向きなので符合は+となります。
\(\vec{F}_y\)はy軸の正の向きなので符合は+となります。
よって、
\(\displaystyle{\begin{eqnarray}\vec{F}_x&=&+|\vec{F}_x|\\\\&=&+2\sqrt{3}N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\vec{F}_y&=&+|\vec{F}_y|\\\\&=&+2N\end{eqnarray}}\)
となります。
※それぞれ、x軸方向とy軸方向での一次元で考えた場合上記のようになります。
二次元で考えた場合、それぞれ\(\vec{F}_x\)のy成分は0、\(\vec{F}_y\)のx成分は0となります
\(\vec{F}\)を成分表示すると、x成分の値は\(\vec{F}_x\)、y成分の値は\(\vec{F}_y\)となるので
\(\displaystyle{\begin{eqnarray}\vec{F}&=&\left(\begin{array}{c}F_x\\F_y\end{array}\right)\\\\&=&\left(\begin{array}{l}+2\sqrt{3}N\\+2N\end{array}\right)\end{eqnarray}}\)
となります。
2-2.問題2
\(\underline{\bf{問題2}}\)
下図の力をx軸方向のベクトル\(\vec{F}_x\)とy軸方向のベクトル\(\vec{F}_y\)に分解し図示せよ。
また、\(\vec{F}\)をx成分とy成分で表示せよ。
ただし、図中の\(\vec{F}\)の大きさは
\(|\vec{F}|=6N\)
とする。
(N(ニュートン)は力の単位)
\(\underline{\bf{解答2}}\)
問題1と同様にして、x軸とy軸に平行な辺を持つ四角形を作成し、ベクトルを分解すると下図のようになります。
分解したそれぞれのベクトルの大きさは、同様にして三角関数を用いて、
\(\displaystyle{\begin{eqnarray}|\vec{F}_x|&=&|\vec{F}|\cos60°\\\\&=&6N×\frac{1}{2}\\\\&=&3N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}|\vec{F}_y|&=&|\vec{F}|\sin60°\\\\&=&6N×\frac{\sqrt{3}}{2}\\\\&=&3\sqrt{3}N\end{eqnarray}}\)
次に、ベクトルの符合を考えます。
\(\vec{F}_x\)はx軸の負の向きなので符合は-となります。
\(\vec{F}_y\)はy軸の正の向きなので符合は+となります。
よって、
\(\displaystyle{\begin{eqnarray}\vec{F}_x&=&-|\vec{F}_x|\\\\&=&-3N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\vec{F}_y&=&+|\vec{F}_y|\\\\&=&+3\sqrt{3}N\end{eqnarray}}\)
となります。
※それぞれ、x軸方向とy軸方向での一次元で考えた場合上記のようになります。
二次元で考えた場合、それぞれ\(\vec{F}_x\)のy成分は0、\(\vec{F}_y\)のx成分は0となります
\(\vec{F}\)を成分表示すると、x成分の値は\(\vec{F}_x\)、y成分の値は\(\vec{F}_y\)となるので
\(\displaystyle{\begin{eqnarray}\vec{F}&=&\left(\begin{array}{c}\vec{F}_x\\\vec{F}_y\end{array}\right)\\\\&=&\left(\begin{array}{l}-3N\\+3\sqrt{3}N\end{array}\right)\end{eqnarray}}\)
となります。
※三角関数の単位円と同じようにして角度をとると、符合の情報も含んだ値となります。
すなわち、下図のように角度をとります。
(180°-60°=120°となっている)
このように角度をとると、三角関数が符合の情報も含むので\(\vec{F}_x\)と\(\vec{F}_y\)はそれぞれ
\(\displaystyle{\begin{eqnarray}\vec{F}_x&=&|\vec{F}|\cos120°\\\\&=&6N×\left(-\frac{1}{2}\right)\\\\&=&-3N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\vec{F}_y&=&|\vec{F}|\sin120°\\\\&=&6N×\left(+\frac{\sqrt{3}}{2}\right)\\\\&=&+3\sqrt{3}N\end{eqnarray}}\)
となります。
2-3.問題3
\(\underline{\bf{問題3}}\)
下図の力をx軸方向のベクトル\(\vec{F}_x\)とy軸方向のベクトル\(\vec{F}_y\)に分解し図示せよ。
また、\(\vec{F}\)をx成分とy成分で表示せよ。
ただし、図中の\(\vec{F}\)の大きさは
\(|\vec{F}|=2N\)
とする。
(N(ニュートン)は力の単位)
\(\underline{\bf{解答3}}\)
問題1と同様にして、x軸とy軸に平行な辺を持つ四角形を作成し、ベクトルを分解すると下図のようになります。
分解したそれぞれのベクトルの大きさは、同様にして三角関数を用いて、
\(\displaystyle{\begin{eqnarray}|\vec{F}_x|&=&|\vec{F}|\cos45°\\\\&=&2N×\frac{1}{\sqrt{2}}\\\\&=&\sqrt{2}N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}|\vec{F}_y|&=&|\vec{F}|\sin45°\\\\&=&2N×\frac{1}{\sqrt{2}}\\\\&=&\sqrt{2}N\end{eqnarray}}\)
次に、ベクトルの符合を考えます。
\(\vec{F}_x\)はx軸の正の向きなので符合は+となります。
\(\vec{F}_y\)はy軸の負の向きなので符合は-となります。
よって、
\(\displaystyle{\begin{eqnarray}\vec{F}_x&=&-|\vec{F}_x|\\\\&=&+\sqrt{2}N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\vec{F}_y&=&+|\vec{F}_y|\\\\&=&-\sqrt{2}N\end{eqnarray}}\)
となります。
※それぞれ、x軸方向とy軸方向での一次元で考えた場合上記のようになります。
二次元で考えた場合、それぞれ\(\vec{F}_x\)のy成分は0、\(\vec{F}_y\)のx成分は0となります
\(\vec{F}\)を成分表示すると、x成分の値は\(\vec{F}_x\)、y成分の値は\(\vec{F}_y\)となるので
\(\displaystyle{\begin{eqnarray}\vec{F}&=&\left(\begin{array}{c}\vec{F}_x\\\vec{F}_y\end{array}\right)\\\\&=&\left(\begin{array}{l}+\sqrt{2}N\\-\sqrt{2}N\end{array}\right)\end{eqnarray}}\)
となります。
※三角関数の単位円と同じようにして角度をとると、符合の情報も含んだ値となります。
すなわち、下図のように角度をとります。
(360°-45°=315°となっている)
このように角度をとると、三角関数が符合の情報も含むので\(\vec{F}_x\)と\(\vec{F}_y\)はそれぞれ
\(\displaystyle{\begin{eqnarray}\vec{F}_x&=&|\vec{F}|\cos315°\\\\&=&6N×\left(+\frac{1}{\sqrt{2}}\right)\\\\&=&+\sqrt{2}N\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\vec{F}_y&=&|\vec{F}|\sin315°\\\\&=&6N×\left(-\frac{1}{\sqrt{2}}\right)\\\\&=&-\sqrt{2}N\end{eqnarray}}\)
となります。
はてなブログ内関連記事
5.力とベクトル
力とは、物体の状態を変化させる原因となるものとなります。
これまでに、変位や速度、加速度がベクトルであると述べてきましたが、この力もベクトルとなります。
この記事では、基本的なベクトルの扱い方や、力の合成、分解について解説していきます。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.力とは
静止している物体に力を加えると物体は動き出します。
また、動いている物体に力を加えると、物体の速さや運動の向きが変わります。
上記のように、力とは物体の状態(静止しているor運動している、速さ、運動の向きなど)を変化させる原因となるものとなります。
また、力は速度や加速度と同様に向きと大きさをもつベクトルとなります。
向きは矢印の向きで、大きさは矢印の長さで表現します。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
これから物理で必要なベクトルについて解説していきますが、ベクトルは数学で扱うので、厳密な定義や扱い方は数学の方で学んでください。
以下のような\(x-y\)座標上のベクトルを考えます。
赤色の矢印を\(\textcolor{red}{\vec{F_1}}\)(エフワンベクトル)とします。
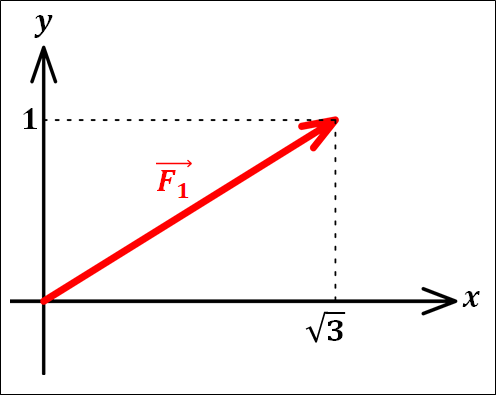
\(\textcolor{red}{\vec{F_1}}\)の向きは、図中の矢印の向きになります。
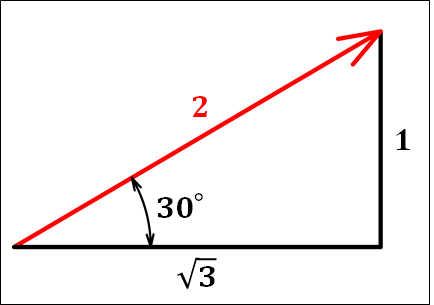
ちなみに、図中の直角三角形に注目すると、三角関数から
となるので、\(x\)軸と\(30°\)の角をなす方向であることが分かります。
(三角関数については、こちらも参考にしてください→三角関数の定義と関係式)
\(\textcolor{red}{\vec{F_1}}\)の大きさ\(\textcolor{red}{|\vec{F_1}|}\)は矢印の長さになります。
こちらも先ほどの直角三角形の図をみると、大きさは\(2\)となります。
(\(\textcolor{red}{|\vec{F_1}|=2}\)。三平方の定理から導ける)
また、矢印の先端から\(x\)軸、\(y\)軸上に垂直な線を引くと、\(\sqrt{3}\)、\(1\)と交わっています。
(\(x\)座標が\(\sqrt{3}\)。\(y\)座標が\(1\)。)
この\(x\)座標と\(y\)座標の値をそれぞれ\(\textcolor{red}{\vec{F_1}}\)の\(x\)成分、\(y\)成分といいます。
なので、\(\textcolor{red}{\vec{F_1}}\)の\(x\)成分は\(\sqrt{3}\)、\(y\)成分は\(1\)となります。
ベクトルの成分表示はいろいろありますが、物理では
\(\displaystyle{\textcolor{red}{\vec{F}}=\left(\begin{eqnarray}&&x\bf{成分}\\&&y\bf{成分}\end{eqnarray} \right)}\)
という、縦に並べた表記が有効です。
例で扱った\(\textcolor{red}{\vec{F_1}}\)で表記すると
\(\displaystyle{\textcolor{red}{\vec{F_1}}=\left(\begin{eqnarray}&&\sqrt{3}\\&& 1\end{eqnarray}\right)}\)
となります。
他の表記としては、
\((x,y)=(\sqrt{3},1)\)
や
\(\displaystyle{\left\{\begin{eqnarray}&&x=\sqrt{3}\\&&y=1\end{eqnarray}\right.}\)
などがあります。
2.力の合成
力はベクトルなので、ベクトルの加法のように計算することができます。
力の合成(ベクトルの合成)は、2つのベクトルを2辺とする平行四辺形を描いて行うことができます。
また、合成した力を"合力"といいます。
下図で説明していきます。
\(\textcolor{blue}{\vec{F_1}}\)と\(\textcolor{blue}{\vec{F_2}}\)の合力\(\textcolor{red}{\vec{F}}\)を、平行四辺形を描いて求めてみます。
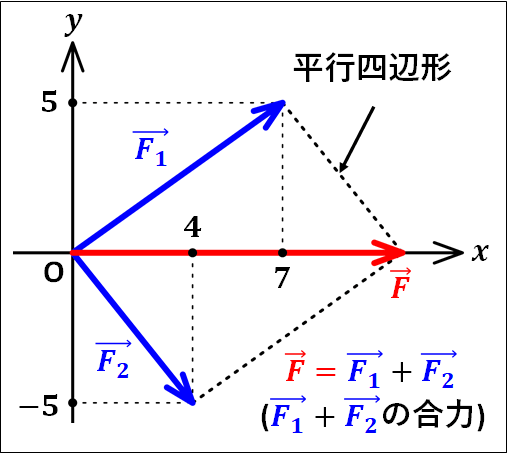
↓
ベクトルは平行移動させてもよいので、\(\textcolor{blue}{\vec{F_1}}\)だけ進んだところから、\(\textcolor{blue}{\vec{F_2}}\)だけ進んだベクトルであると考えることもできます。
↓
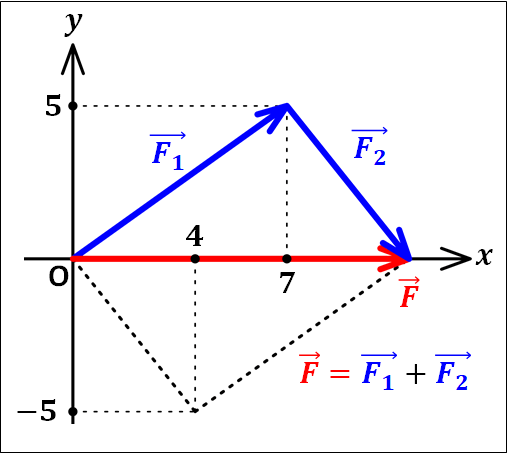
上図のように、平行四辺形を描いて矢印の始まりの点と平行四辺形の対角の点を結んだものが合力となります。
今回は図示する上で2つの力を扱いましたが、力はいくつでも、それぞれ任意の(すきな)2力の合成を続けていくことで、合力を求めていくことができます。
例えば\(\vec{F_1}\)と\(\vec{F_2}\)と\(\vec{F_3}\)の合力を図示する場合、まずは\(\vec{F_1}\)と\(\vec{F_2}\)の合力を図示し(この合力を\(\vec{F_{12}}\)とする)、そのあと\(\vec{F_{12}}\)と\(\vec{F_3}\)の合力を図示することで3力の合力を図示することができます。
次に成分を考えていきます。
図から
\(\displaystyle{\textcolor{blue}{\vec{F_1}=\left(\begin{eqnarray}&&7\\&&5\end{eqnarray}\right)}}\)
\(\displaystyle{\textcolor{blue}{\vec{F_2}=\left(\begin{eqnarray}&& 4\\&&-5\end{eqnarray}\right)}}\)
なので、\(\textcolor{blue}{\vec{F_1}}\)と\(\textcolor{blue}{\vec{F_2}}\)の合力\(\textcolor{red}{\vec{F}}\)の成分は、
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{F}}&=&\textcolor{blue}{\vec{F_1}+\vec{F_2}}\\\\&=&\textcolor{blue}{\left(\begin{eqnarray}&&7\\&&5\end{eqnarray}\right)}+\textcolor{blue}{\left(\begin{eqnarray}&& 4\\&&-5\end{eqnarray}\right)}\\\\&=&\textcolor{red}{\left(\begin{eqnarray}&&11\\&&0\end{eqnarray}\right)}\end{eqnarray}}\)
となります。
物理では力や速度でベクトルを扱いますが、斜め方向などのベクトルは扱いにくいので、成分での計算を行うことが多いです。
なので問題を解く中で、現在ベクトルそのものを扱っているのか、あるいはベクトルの成分を扱っているのかということに注意しておくと良いと思います。
3.力の分解
力の分解も平行四辺形を描くことで、任意の(すきな)2方向に分けることができます。
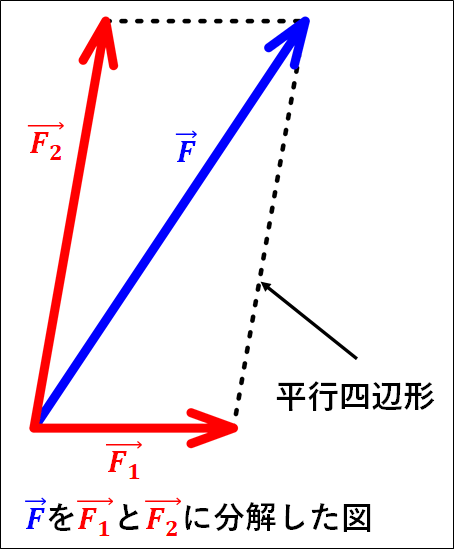
上図は、\(\textcolor{blue}{\vec{F}}\)を\(\textcolor{red}{\vec{F_1}}\)と\(\textcolor{red}{\vec{F_2}}\)に分解した図となります。
\(\textcolor{blue}{\vec{F}}\)を対角線とする平行四辺形を描くことで、この対角線であるベクトルを平行四辺形を形作る2辺に沿うベクトルに分解できます。
分解されたベクトルは、もとのベクトルと始点は一致しており、終点は平行四辺形の頂点となります。
また、ベクトルは平行移動させても変わらないので、\(\textcolor{red}{\vec{F_1}}\)と\(\textcolor{red}{\vec{F_2}}\)は下図のようにも表せます。
力の合成の部分でみた図に関して、
\(\vec{F_1}+\vec{F_2}=\vec{F}\)
は力の合成となりますが\(\vec{F_1}\)と\(\vec{F_2}\)は\(\vec{F}\)を2力に分解したものであるとみることもできます。
先ほど、物理では成分で扱うことが多いと述べましたが、ベクトルを成分で扱うために力の分解を行うことが多いです。
たいていは、水平方向と鉛直方向にベクトルを分解し、複数の力を水平方向の成分のみで考える、鉛直方向の成分のみで考える、とします。
なので、"ふつうは直交方向(直角に交わる方向)"にベクトルを分解します。
直角方向の分解に関して、特に\(\vec{F}\)を斜辺とする直角三角形の隣辺方向と対辺方向に分解するとき、隣辺と\(\vec{F}\)のなす角が\(\theta\)の際には、分解した2つのベクトルは\(\vec{F}\)の大きさ\(|\vec{F}|\)を用いて次のようになります。
(今回は\(x-y\)座標で表したので、隣辺方向のベクトル(\(x\)成分)を\(\vec{F_x}\)、対辺方向のベクトル(\(y\)成分)を\(\vec{F_y}\)としています。)
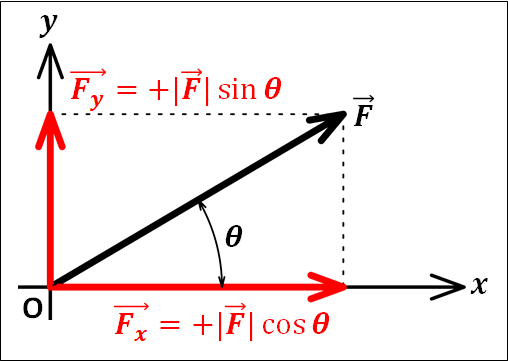
いま、分解したベクトルはそれぞれ\(x\)軸の正方向の向きと\(y\)軸の正方向の向きになるので、これらはどちらも正となります。
また、分解したベクトルを用いてもとのベクトル\(\vec{F}\)を成分表示すると
\(\displaystyle{\vec{F}=\left(\begin{eqnarray}&&\textcolor{red}{+|\vec{F}|\cos\theta}\\&&\textcolor{red}{+|\vec{F}|\sin\theta}\end{eqnarray}\right)}\)
となります。
上記の直角三角形を作ってベクトルを分解する際の覚え方を載せておきます。
(三角関数の定義から計算することもできますが、これぐらいは覚えておいてもいいと思います)
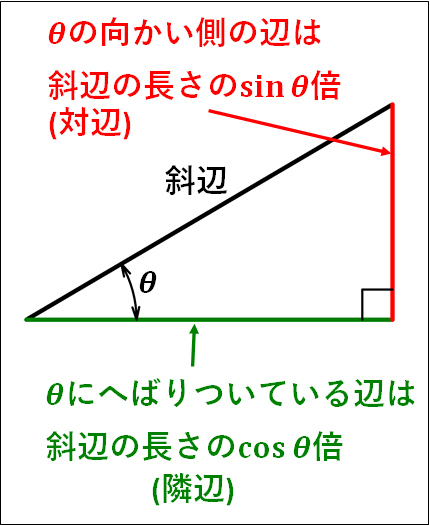
直角三角形を用いた各辺の長さとベクトルの分解については、こちらも参考にしてください。
→三角関数の定義と関係式
→練習問題1(三角関数の定義とグラフ)
→練習問題(ベクトル)
はてなブログ内関連記事
4-2.落下運動①(補足解説と練習問題2)
落下運動①の記事で解説した内容の練習問題となります。
今回は、2物体の落下運動と少し複雑なv-tグラフについて取り扱います。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、落下運動①の記事で解説していなかった補足内容があれば、この記事に載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.2物体の落下運動
1-1.問題1
\(\underline{\bf{問題1}}\)
高い建物の屋上から、物体Aを静かに放し、その2.0秒後に物体Bを初速度28m/sで鉛直下向きに投げ下ろした。
このとき、物体Bを投げ下ろしてから何秒後に物体Bは物体Aに追いつくか答えよ。
また、追いついたときの物体Bの速さはいくらか答えよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答1}}\)
いままでは1つの物体についての落下運動でしたが、今回は物体が2つの場合を扱います。
原点は物体のスタート地点、物体は両方とも鉛直下向きに運動するので、下向きを正とします。
下向きを正としているので、重力加速度は\(+9.8m/s^2\)と正の値になります。
物体Bを投げてから追いつくまでの時間をt[s]とすると、状況は下図のようになります。
ここで、v-tグラフを描くために2.0s後の物体Aの速度を考えます。
このときの物体Aの速度を\(v_A\)とすると、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+9.8m/s^2=\frac{v_A-0m/s}{2.0s-0s}\\\\{\Leftrightarrow}&&v_A=9.8m/s^2×2.0s\\\\{\Leftrightarrow}&&v_A=19.6m/s\end{eqnarray}}\)
前述のとおり、物体Bを投げてから物体Aに追いつくまでの時間をt[s]とし、また、追いついたときの物体Bの速度を\(v_B\)とするとv-tグラフは下図のようになります。
(両物体ともv-tグラフの傾きは\(+9.8m/s^2\))
ここで少し考えます。
追いつくというのはv-tグラフでいうと、どのような条件になるでしょうか?
追いついたときには、物体Aも物体Bも同じ高さにいます。
ということは、建物の屋上からの進んだ距離が同じになるということです。
v-tグラフの面積は、進んだ距離を表すので、"物体Aのv-tグラフの面積と物体Bのv-tグラフの面積が等しくなる"というのが、追いつく条件となります。
上図において、青色斜線部は共通なので、結局下図の部分が等しければよいことになります。
(図形の両辺から、青色斜線部を引いても等号は成り立つ)
赤色斜線部は直角三角形の面積です。
緑色斜線部は、両物体のv-tグラフの傾きが\(+9.8m/s^2\)と等しく、平行になるので平行四辺形になります。
以上から、面積が等しいという式を立てると
\(\displaystyle{\begin{eqnarray}&&2.0s×19.6m/s×\frac{1}{2}=t×8.4m/s\\\\{\Leftrightarrow}&&19.6m=t×8.4m/s\\\\{\Leftrightarrow}&&t=\frac{19.6m}{8.4m/s}\\\\{\Leftrightarrow}&&t=\frac{7}{3}s\\\\{\Leftrightarrow}&&t=2.33\cdots{s}\\\\{\Leftrightarrow}&&t≒2.3s\end{eqnarray}}\)
これで、物体Bを投げてから追いつくまでの時間がわかりました。
次に、物体Bの追いついたときの速さを知りたいので、物体Bを投げたときを"はじめ"、追いついたときを"あと"と考えると、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+9.8m/s^2=\frac{v_B-28m/s}{t[s]}\\\\{\Leftrightarrow}&&+9.8m/s^2=\frac{v_B-28m/s}{2.33s}\\\\{\Leftrightarrow}&&v_B=9.8m/s^2×2.33s+28m/s\\\\{\Leftrightarrow}&&v_B=22.84m/s+28m/s\\\\{\Leftrightarrow}&&v_B=50.84m/s\\\\{\Leftrightarrow}&&v_B≒51m/s\end{eqnarray}}\)
以上から
物体Bを投げてから物体Aに追いつくまでの時間
\(\underline{2.3秒後}\)
追いついた時の物体Bの速さ
\(\underline{51m/s}\)
となります。
1-2.問題2
\(\underline{\bf{問題2}}\)
建物の屋上から、物体Aを静かに放すと同時に、地面から物体Bを真上に初速度28m/sで投げ上げると、高さ40mの点で両物体は衝突した。
物体Aと物体Bは同一直線上を運動するとし、重力加速度の大きさを\(9.8m/s^2\)、空気抵抗は無視できるとき、次の問に答えよ。
ただし、鉛直上向きを正とする。
(1)物体Aと物体Bが衝突するのは、物体が運動をはじめてから何秒後か。
(2)衝突直前の物体Aと物体Bの速度を答えよ。
(3)建物の高さは何mか。
\(\underline{\bf{解答2}}\)
2物体を扱うときの軸の取り方は、両物体とも同じ向きを正とします。
今回は、鉛直上向きを正とするとのことなので、上向きが正となります。
原点は物体が運動をはじめる位置にとるので、状況は下図のようになります。
物体Aは自由落下。
物体Bは初速度+28m/sでの鉛直投げ上げとなります。
いま、鉛直上向きを正としているので、両物体の重力加速度は\(-9.8m/s^2\)となります。
また、高さ40mで衝突したということは、物体Bが進んだ距離が40m、すなわち物体Bのv-tグラフの面積が40mになるということです。
以上から、衝突直前の物体Aの速度を\(v_A\)、衝突直前の物体Bの速度を\(v_B\)、衝突時刻をtとすると両物体のv-tグラフは下図のようになります。
(1)
物体Bに関する加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{v_B-28m/s}{t-0s}\\\\{\Leftrightarrow}&&v_B=28m/s-9.8m/s^2×t \cdots①\end{eqnarray}}\)
物体Bに関する、v-tグラフの面積から(台形の面積)
\(\displaystyle{\begin{eqnarray}&&+40m=\frac{1}{2}t(v_B+28m/s)\\\\{\Leftrightarrow}&&80m=t(v_B+28m/s) \cdots②\end{eqnarray}}\)
①を②に代入して、
\(\displaystyle{\begin{eqnarray}&&80=t(v_B+28)\\\\{\Leftrightarrow}&&80=t(28-9.8t+28)\\\\{\Leftrightarrow}&&80=t(56-9.8t)\\\\{\Leftrightarrow}&&80=56t-9.8t^2\\\\{\Leftrightarrow}&&9.8t^2-56t+80=0\\\\{\Leftrightarrow}&&98t^2-560t+800\\\\{\Leftrightarrow}&&49t^2-280t+400=0\\\\{\Leftrightarrow}&&(7t)^2-2・(7t)・(20)^2=0\end{eqnarray}}\)
ここで、
\(7t=a\)
\(20=b\)
とおくと、
\(\displaystyle{\begin{eqnarray}&&(7t)^2-2・(7t)・(20)^2=0\\\\{\Leftrightarrow}&&a^2-2ab+b^2\\\\{\Leftrightarrow}&&(a-b)^2=0\\\\{\Leftrightarrow}&&(7t-20)^2=0\end{eqnarray}}\)
よって、
\(\displaystyle{\begin{eqnarray}&&7t-20=0\\\\{\Leftrightarrow}&&7t=20\\\\{\Leftrightarrow}&&t=\frac{20}{7}s\\\\{\Leftrightarrow}&&t≒2.85s\\\\{\Leftrightarrow}&&t≒2.9s\end{eqnarray}}\)
以上から、物体が衝突する時刻は、物体が運動をはじめてから
\(\underline{\bf{2.9秒後}}\)
(2)
物体Bに関しては、(1)から\(t=\frac{20}{7}s\)を①に代入して
\(\displaystyle{\begin{eqnarray}v_B&=&28m/s-9.8m/s^2×t\\\\&=&28m/s-9.8m/s×\frac{20}{7}\\\\&=&28m/s-98×\frac{2}{7}m/s\\\\&=&28m/s-14×2m/s\\\\&=&28m/s-28m/s\\\\&=&0m/s\end{eqnarray}}\)
このことから、物体Bが最高点に到達したときに、両物体が衝突したことがわかります。
(投げ上げたあとに、速度が0m/sとなるので)
物体Aについては、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{v_A-0m/s}{t-0s}\\\\{\Leftrightarrow}&&v_A=-9.8m/s^2×t\\\\{\Leftrightarrow}&&v_B=-9.8m/s^2×\frac{20}{7}s\\\\{\Leftrightarrow}&&v_A=-28m/s\end{eqnarray}}\)
以上から
衝突直前の物体Aの速度
\(\underline{\bf{-28m/s}}\)
衝突直前の物体Bの速度
\(\underline{\bf{0m/s}}\)
(3)
建物の高さは、物体Aが下向きに進んだ距離と、物体Bが上向きに進んだ距離の和となります。
物体Aが進んだ距離\(h_A\)は、v-tグラフの三角形の面積から
\(\displaystyle{\begin{eqnarray}h_A&=&\frac{1}{2}×v_A×t\\\\&=&\frac{1}{2}×(-28m/s)×\frac{20}{7}s\\\\&=&-40m\end{eqnarray}}\)
いま、鉛直上向きを正としているので、符合のマイナスは物体Aが下向きに進んだ距離となります。
物体Bが上向きに進んだ距離は40mなので、建物の高さHは
\(\displaystyle{\begin{eqnarray}H&=&40m+|-40m|\\\\&=&40m+40m\\\\&=&80m\end{eqnarray}}\)
よって、建物の高さは
\(\underline{\bf{80m}}\)
※(3)の別解
40mで衝突したとき、たまたま物体Bは最高点で衝突しています。
このとき、v-tグラフにおいて三角形ができるので、三角形の相似を使いたいと思い、v-tグラフを描きなおしてみます。
v-tグラフを描きなおすと下図のようになります。
v-tグラフを眺めてみると、建物の高さである物体Aの面積と物体Bの面積は平行四辺形であることがわかります。
よって、平行四辺形の面積を求める式を用いて、建物の高さHは
\(\displaystyle{\begin{eqnarray}H&=&t×28m/s\\\\&=&\frac{20}{7}s×28m/s\\\\&=&80m\end{eqnarray}}\)
よって、建物の高さは
\(\underline{\bf{80m}}\)
となります。
2.複雑なv-tグラフの解釈
\(\underline{\bf{問題}}\)
風船に物体を取り付け、上昇させることを考える。
風船と物体は地上から鉛直上向きに初速度0、一定の加速度で上昇するとする。
60秒後、地上からの高さ147mに到達したとき、物体は風船から静かに切り離された。
このとき、次の問に答えよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
(1)上昇中の風船と物体の加速度を答えよ。
(2)風船から物体が静かに切り離されたときの、物体の速度を答えよ。
(3)物体が最高点に到達するのは、風船から物体が切り離されてから何秒後か。
(4)物体が地面に到達するのは、風船から物体が切り離されてから何秒後か。
\(\underline{\bf{解答}}\)
風船と物体ははじめ鉛直上向きに上昇するので、鉛直上向きを正とします。
また、風船から物体が切り離される直前までは、物体は一定の加速度で上昇します。
風船が物体から切り離されてからは、物体は自由落下します。
物体が自由落下している際は、鉛直上向きを正としているので、重力加速度は\(-9.8m/s^2\)となります。
状況を図示すると、下図のようになります。
次にv-tグラフを考えていきます。
i)物体が切り離されるまで
物体が切り離されるまでは、風船と物体は一体となって一定の加速度で上昇します。
この加速度をαとしておきます。
いま鉛直上向きを正としているので、v-tグラフの傾きは右上がりとなります。
また、60秒後の風船と物体の速度をvとします。
ii)物体が切り離されてから
物体が切り離される直前、風船と物体の速度はvなので、切り離された直後の物体の速度はvとなります。
また、物体は自由落下します。
いま鉛直上向きを正としているので、加速度は(-9.8m/s^2)となり、v-tグラフの傾きは右下がりとなります。
物体が切り離されてから上昇する距離をh、物体が切り離されてから最高点に到達する時間を\(t\)、物体が切り離されてから地面に落下するまでの時間を\(t^{\prime}\)とすると、v-tグラフは下図のようになります。
(問われている時間を文字で設定した)
このv-tグラフをもとにして、問題を解いていきます。
(1)
風船と物体の加速度は、物体が切り離されるまでのv-tグラフにおける加速度の定義式から
\(\displaystyle{\begin{eqnarray}a&=&\frac{v-0m/s}{60s-0s}\\\\&=&\frac{v}{60s} \cdots①\end{eqnarray}}\)
また、物体が切り離されるまでのv-tグラフの面積から
\(\displaystyle{\begin{eqnarray}&&+147m=\frac{1}{2}×60s×v\\\\{\Leftrightarrow}&&v=\frac{2×147m}{60s}\\\\{\Leftrightarrow}&&v=4.9m/s \cdots②\end{eqnarray}}\)
②を①に代入して
\(\displaystyle{\begin{eqnarray}v&=&\frac{v}{60s}\\\\&=&\frac{4.9m/s}{60s}\\\\&=&0.0816m/s^2\\\\&≒&8.2×10^{-2}m/s^2\end{eqnarray}}\)
よって、上昇中の風船と物体の加速度は
\(\underline{\bf{8.2×10^{-2}m/s^2}}\)
(2)
風船から物体が静かに切り離されたときの、物体の速度はvなので、(1)の②から
\(v=+4.9m/s\)
いま鉛直上向きを正としており、速度の符合は+なので、鉛直上向きの速度4.9m/sとなります。
よって、求める速度は
\(\underline{\bf{鉛直上向きに4.9m/s}}\)
(3)
v-tグラフにおいて、物体が切り離されてから最高点に到達するまでに注目すると、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{0m/s-v}{t}\\\\{\Leftrightarrow}&&-9.8m/s^2=\frac{0m/s-4.9m/s}{t}\\\\{\Leftrightarrow}&&-9.8m/s^2=\frac{-4.9m/s}{t}\\\\{\Leftrightarrow}&&t=\frac{-4.9m/s}{-9.8m/s^2}\\\\{\Leftrightarrow}&&t=0.50s\end{eqnarray}}\)
よって、風船から物体が切り離されてから物体が最高点に到達するのは
\(\underline{\bf{0.50秒後}}\)
(4)
三角形の相似を用います。
相似な三角形の"辺の長さの比"と"面積"の関係について
\(\displaystyle{(辺の長さの比)^2=(面積の比)}\)
が成り立ちます。
今回は、物体が切り離されてから最高点に到達するまでと、最高点に到達してから地面に到達するまでのv-tグラフにおける三角形の相似に注目します。
また、上記の面積hについて、v-tグラフの面積を求める式から
\(\displaystyle{\begin{eqnarray}h&=&\frac{1}{2}vt\\\\&=&\frac{1}{2}×4.9m/s×0.5s\\\\&=&\frac{4.9}{4}m\\\\&=&\frac{49}{40}m\end{eqnarray}}\)
相似な三角形の"辺の長さの比"と"面積"の関係を用いると、
\(\displaystyle{{\left(\frac{t^{\prime}-t}{t}\right)}^2=\frac{h+147}{h} \cdots③}\)
上式の右辺について
\(\displaystyle{\begin{eqnarray}\frac{h+147}{h}&=&\frac{h}{h}+\frac{147}{h}\\\\&=&1+\frac{147}{\frac{49}{40}}\\\\&=&1+147×\frac{40}{49}\\\\&=&1+120\\\\&=&121\\\\&=&11^2\end{eqnarray}}\)
よって③式は
\(\displaystyle{{\left(\frac{t^{\prime}-t}{t}\right)}^2=11^2}\)
上式から
\(\displaystyle{\begin{eqnarray}&&\frac{t^{\prime}-t}{t}=11\\\\{\Leftrightarrow}&&t^{\prime}-t=11t\\\\{\Leftrightarrow}&&t^{\prime}=t+11t\\\\{\Leftrightarrow}&&t^{\prime}=12t\\\\{\Leftrightarrow}&&t^{\prime}=12×0.5s\\\\{\Leftrightarrow}&&t^{\prime}=6s\end{eqnarray}}\)
これより、風船から物体が切り離されてから地面に到達するのは
\(\underline{\bf{6.0秒後}}\)
※(4)を三角形の相似を用いずに解くと、
面積hについて、同様の計算を行って
\(\displaystyle{h=\frac{40}{49}m}\)
物体が地面に到達したときの速度を\(v_{あと}\)とし、v-tグラフにおける物体が最高点に到達してから地面に到達するまでに注目すると
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8=\frac{v_{あと}-0m/s}{t^{\prime}-t}\\\\{\Leftrightarrow}&&v=-9.8×(t^{\prime}-t) \cdots④\end{eqnarray}}\)
面積を求める式から
\(\displaystyle{-h-147=\frac{1}{2}v_{あと}(t^{\prime}-t) \cdots⑤}\)
④を⑤に代入して
\(\displaystyle{\begin{eqnarray}&&-h-147=\frac{1}{2}v_{あと}×(t^{\prime}-t)\\\\{\Leftrightarrow}&&-h-147=\frac{1}{2}×(-9.8)×(t^{\prime}-t)^2\\\\{\Leftrightarrow}&&(t^{\prime}-t)^2=\frac{2(h+147)}{9.8} \cdots⑥\end{eqnarray}}\)
上式右辺について
\(\displaystyle{\begin{eqnarray}\frac{2(h+147)}{9.8}&=&\frac{h+147}{4.9}\\\\&=&\frac{h}{4.9}+\frac{147}{4.9}\\\\&=&\frac{49}{40×4.9}+30\\\\&=&\frac{1}{4}+30\\\\&=&\frac{1+120}{4}\\\\&=&\frac{121}{4}\\\\&=&\frac{11^2}{2^2}\\\\&=&{\left(\frac{11}{2}\right)}^2\end{eqnarray}}\)
よって⑥式は
\(\displaystyle{(t^{\prime}-t)^2={\left(\frac{11}{2}\right)}^2}\)
以上から
\(\displaystyle{\begin{eqnarray}&&t^{\prime}-t=\frac{11}{2}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{11}{2}+t\\\\{\Leftrightarrow}&&t^{\prime}=\frac{11}{2}+\frac{1}{2}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{12}{2}\\\\{\Leftrightarrow}&&t^{\prime}=6\end{eqnarray}}\)
以上より、風船から物体が切り離されてから地面に到達するのは
\(\underline{\bf{6.0秒後}}\)
はてなブログ内関連記事
4-1.落下運動①(補足解説と練習問題1)
落下運動①の記事で解説した内容の練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、落下運動①の記事で解説していなかった補足内容があれば、この記事に載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.自由落下
1-1.問題1
\(\underline{\bf{問題1}}\)
ある高さの建物の屋上から物体を静かに放すと、物体は落下し5.0秒後に地面に到達した。
このときの建物の高さと、物体が地面に到達する直前の速さを求めよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答1}}\)
原点と軸の設定をします。
原点は物体を放す位置とし、物体は放した後落下するので下向きを正とします。
また、重力加速度は下向きであり、軸も下向きを正としたので重力加速度の符合は正となります。
静かに放すとは、初速度を加えていないということなので、はじめとあとの状況を整理すると
はじめ:t=0sでv=0m/s
あと:t=5.0sで\(v=v_{あと}\)
また、建物の高さをyとすると、これがv-tグラフの面積となるので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+9.8m/s^2=\frac{v_{あと}-0m/s}{5.0s-0s}\\\\{\Leftrightarrow}&&v_{あと}=49m/s\end{eqnarray}}\)
v-tグラフの面積から
\(\displaystyle{\begin{eqnarray}y&=&\frac{1}{2}×5.0s×v_{あと}\\\\&=&\frac{1}{2}×5.0s×49m/s\\\\&=&122.5m\\\\&≒&1.2×10^2m\end{eqnarray}}\)
以上から
建物の高さ
\(\underline{1.2×10^2m}\)
地面に到達する直前の速さ
\(\underline{49m/s}\)
1-2.問題2
\(\underline{\bf{問題2}}\)
高さ40mの建物の屋上から物体を静かに放すと、物体は落下し地面に到達した。
このとき、物体が地面に到達するまでの時間と、地面に到達する直前の速さを求めよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答2}}\)
前問と同様にして、軸と原点の設定をすると、下図のようになります。
また、はじめとあとの状況を整理すると
はじめ:t=0sでv=0m/s
あと:\(t=t_{あと}\)で\(v=v_{あと}\)
建物の高さである40mは、v-tグラフの面積となります。
以上から、v-tグラフは下図のようになります。
これより、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+9.8m/s^2=\frac{v_{あと}-0m/s}{t_{あと}-0s}\\\\{\Leftrightarrow}&&v_{あと}=9.8m/s^2×t_{あと} \cdots①\end{eqnarray}}\)
v-tグラフの面積の式から
\(\displaystyle{\begin{eqnarray}&&40m=\frac{1}{2}v_{あと}t_{あと}\\\\{\Leftrightarrow}&&80m=v_{あと}t_{あと} \cdots②\end{eqnarray}}\)
①、②から
\(\displaystyle{\begin{eqnarray}&&80m=v_{あと}t_{あと}\\\\{\Leftrightarrow}&&80m=(9.8m/s^2×t_{あと})×t_{あと}\\\\{\Leftrightarrow}&&t_{あと}^2=\frac{80m}{9.8m/s^2}\\\\{\Leftrightarrow}&&t_{あと}^2=\frac{800}{98}s^2\\\\{\Leftrightarrow}&&t_{あと}^2=\frac{400}{49}s^2\\\\{\Leftrightarrow}&&t_{あと}^2=\frac{20^2}{7^2}\end{eqnarray}}\)
よって、
\(\displaystyle{\begin{eqnarray}t_{あと}&=&\frac{20}{7}s\\\\&≒&2.857s\\\\&≒&2.9s\end{eqnarray}}\)
これを①に代入して
\(\displaystyle{\begin{eqnarray}v_{あと}&=&9.8m/s^2×t_{あと}\\\\&=&9.8m/s^2×2.86s\\\\&≒&28m/s\end{eqnarray}}\)
以上から、
物体が地面に到達するまでの時間
\(\underline{2.9s}\)
地面に到達する直前の速さ
\(\underline{28m/s}\)
1-3.問題3
\(\underline{\bf{問題3}}\)
高さがHの建物の屋上から物体を静かに放すと、物体は落下し地面に到達し、到達直前の速さはV[m/s]であった。
このとき、次の問に答えよ。
ただし、重力加速度の大きさは\(g[m/s^2]\)とし、空気抵抗は無視できるものとする。
(1)
物体の速さが、到達直前の速さの半分のとき、物体の屋上からの距離はいくらか?
(2)
物体を放してから建物の高さの半分の距離を通過するのにかかる時間は、残りの半分の高さを落下し地面に到達するまでの時間の何倍か?
\(\underline{\bf{解答3}}\)
(1)
物体は落下するので、下向きを正とします。
状況を図示すると下図のようになり、原点は建物の屋上とします。
下向きを正としているので、重力加速度は\(+g[m/s^2]\)となり、v-tグラフは右上がりのグラフとなります。
到達直前の速さの半分の時、すなわち\(\frac{1}{2}V\)のときを考え、このときまでに進んだ距離をhとすると、v-tグラフは次にようになります。
求める値はhとなります。
ここでv-tグラフにおける直角三角形の相似に注目します。
注目する直角三角形は、v-tグラフの面積がHとhのものです。
これらの直角三角形は相似となります。
相似な三角形の"辺の長さの比"と"面積"の関係について
\(\displaystyle{(辺の長さの比)^2=(面積の比)}\)
となるので、これを用いると、
\(\displaystyle{\begin{eqnarray}&&\left(\frac{V}{\frac{1}{2}V}\right)^2=\frac{H}{h}\\\\{\Leftrightarrow}&&2^2=\frac{H}{h}\\\\{\Leftrightarrow}&&h=\frac{1}{4}H\end{eqnarray}}\)
従って、到達直前の速さの半分とき、建物の屋上からの距離(物体が下向きに進んだ距離)は
\(\displaystyle{\underline{\frac{1}{4}H}}\)
となります。
(2)
状況設定は(1)とおなじです。
v-tグラフは、屋上の高さの半分を進むのに要した時間を\(t_1\)、さらに半分を進み地面に到達するのに要した時間を\(t_2\)とすると、下図のようになります。
こちらも、直角三角形の相似に注目します。
注目するのは、一辺が\(t_1\)の直角三角形と一辺が\(t_1+t_2\)の直角三角形です。
また、"物体を放してから建物の高さの半分の距離を通過するのにかかる時間は、残りの半分の高さを落下し地面に到達するまでの時間の何倍か"をきかれています。
いま、
"物体を放してから建物の高さの半分の距離を通過するのにかかる時間"を\(t_1\)
"残りの半分の高さを落下し地面に到達するまでの時間"を\(t_2\)
としているので、\(t_1\)は\(t_2\)の何倍かをきかれています。
たとえば、6は3の何倍かをきかれたら
\(6÷3=2\)
となり、"はじめの値(6)÷あとの値(3)"を計算して、2倍となります。
今回も同様にして、はじめの値(\(t_1\))÷あとの値(\(t_2\))、すなわち
\(\displaystyle{\frac{t_1}{t_2}}\)
を求めればよいことになります。
(1)のときと同様にして、相似な三角形の"辺の長さの比"と"面積"の関係、
\(\displaystyle{(辺の長さの比)^2=(面積の比)}\)
を用いると、
\(\displaystyle{\begin{eqnarray}&&\left(\frac{t_1+t_2}{t_1}\right)^2=\frac{H}{\frac{1}{2}H}\\\\{\Leftrightarrow}&&\left(\frac{t_1+t_2}{t_1}\right)^2=2\end{eqnarray}}\)
より、
\(\displaystyle{\begin{eqnarray}&&\frac{t_1+t_2}{t_1}=\sqrt{2}\\\\{\Leftrightarrow}&&t_1+t_2=\sqrt{2}t_1\\\\{\Leftrightarrow}&&t_2=(\sqrt{2}-1)t_1\\\\{\Leftrightarrow}&&\frac{t_1}{t_2}=\frac{1}{\sqrt{2}-1}\\\\{\Leftrightarrow}&&\frac{t_1}{t_2}=\frac{1}{\sqrt{2}-1}×\frac{\sqrt{2}+1}{\sqrt{2}+1}\\\\{\Leftrightarrow}&&\frac{t_1}{t_2}=\frac{\sqrt{2}+1}{2-1}\\\\{\Leftrightarrow}&&\frac{t_1}{t_2}=\sqrt{2}+1\end{eqnarray}}\)
よって、
\(\underline{\sqrt{2}+1{\bf{倍}}}\)
となります。
今回は直角三角形の相似を用いて解きましたが、各時間や速度を自分で設定して、加速度の定義式とv-tグラフの面積を求める式を用いても解くことができます。
例えば、(1)については速さが\(\frac{1}{2}V\)になったときの時刻を\(T_1\)、速さが\(V\)のときの時刻を\(T_2\)とすると、下図のようなv-tグラフになります。
面積がhの直角三角形に注目して、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+g=\frac{\frac{1}{2}V-0m/s}{T_1-0s}\\\\{\Leftrightarrow}&&T_1=\frac{V}{2g} \cdots①\end{eqnarray}}\)
v-tグラフの面積から
\(\displaystyle{h=\frac{1}{2}・\left(\frac{1}{2}V\right)・T_1 \cdots②}\)
①を②に代入して
\(\displaystyle{\begin{eqnarray}h&=&\frac{1}{2}・\left(\frac{1}{2}V\right)・T_1\\\\&=&\frac{1}{2}・\left(\frac{1}{2}V\right)・\frac{V}{2g}\\\\&=&\frac{V^2}{8g} \cdots③\end{eqnarray}}\)
次に、面積がHの直角三角形に注目して、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+g=\frac{V-0m/s}{T_2-0s}\\\\{\Leftrightarrow}&&T_2=\frac{V}{g} \cdots④\end{eqnarray}}\)
v-tグラフの面積から
\(\displaystyle{H=\frac{1}{2}・V・T_2 \cdots⑤}\)
③を⑤に代入して
\(\displaystyle{\begin{eqnarray}H&=&\frac{1}{2}・V・T_2\\\\&=&\frac{1}{2}・V・\frac{V}{g}\\\\&=&\frac{V^2}{2g} \cdots⑥\end{eqnarray}}\)
③÷⑥をして
\(\displaystyle{\begin{eqnarray}&&\frac{h}{H}=\frac{\frac{V^2}{8g}}{\frac{V^2}{2g}}\\\\{\Leftrightarrow}&&\frac{h}{H}=\frac{1}{4}\\\\{\Leftrightarrow}&&h=\frac{1}{4}H\end{eqnarray}}\)
と、同じように答えを導くことができます。
(2)についても、同じようにそれぞれの時点での速度を設定し、加速度の定義式とv-tグラフの面積の式から答えを導くことができます。
2.鉛直投げ下ろし
\(\underline{\bf{問題}}\)
高さ100mの建物の屋上から、ある初速度で物体を鉛直下向きに投げると、4.0秒後に地面にぶつかった。
このときの物体の初速度と地面にぶつかる直前の速さを求めよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答}}\)
初速度を\(v_{はじめ}\)、地面にぶつかる直前の速さを\(v_{あと}\)とし、下図のように軸と原点を設定します。
はじめとあとの情報を整理すると
はじめ:t=0sで\(v=v_{はじめ}\)
あと:t=4.0sで\(v=v_{あと}\)
これより、v-tグラフを描くと下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&+9.8m/s^2=\frac{v_{あと}-v_{はじめ}}{4.0s-0s}\\\\{\Leftrightarrow}&&39.2m/s=v_{あと}-v_{はじめ} \cdots①\end{eqnarray}}\)
v-tグラフの面積から
\(\displaystyle{\begin{eqnarray}&&100m=\frac{1}{2}×4.0s×(v_{あと}+v_{はじめ})\\\\{\Leftrightarrow}&&50m=v_{あと}+v_{はじめ} \cdots②\end{eqnarray}}\)
①+②から
\(\displaystyle{\begin{eqnarray}&&2v_{あと}=89.2m/s\\\\{\Leftrightarrow}&&v_{あと}=44.6m/s\end{eqnarray}}\)
より、地面にぶつかる直前の速さは
\(\underline{45m/s}\)
また、\(v_{あと}=44.6m/s\)を②に代入して
\(\displaystyle{\begin{eqnarray}&&50m/s=v_{あと}+v_{はじめ}\\\\{\Leftrightarrow}&&50m/s=44.6m/s+v_{はじめ}\\\\{\Leftrightarrow}&&v_{はじめ}=50m/s-44.6m/s\\\\{\Leftrightarrow}&&v_{はじめ}=5.4m/s\end{eqnarray}}\)
よって、初速度は
\(\underline{5.4m/s}\)
3.鉛直投げ上げ
3-1.問題1
\(\underline{\bf{問題1}}\)
鉛直上向きにある初速度で物体を打ち上げたところ、高さ40mで最高点に達した。
このときの物体の初速度と、打ち上げてから最高点に達するまでの時間を求めよ。
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答1}}\)
軸の設定をします。
今回は、鉛直上向きに投げているので、この向きを正とします。
その際に、とった軸の正の向きと重力加速度の向きが異なるので、重力加速度は\(-9.8m/s^2\)と負になることに注意します。
最高点の高さ40mは、v-tグラフの面積となります。
また、初速度を\(v_{はじめ}\)、最高点に到達したときの時刻を\(t_{あと}\)としています。
状況を整理すると
はじめ:t=0sで\(v=v_{はじめ}\)
あと:\(t=t_{あと}\)でv=0m/s
このとき、最高点に到達
重力加速度は\(-9.8m/s^2\)と負なので、v-tグラフは右下がりとなります。
v-tグラフを描くと、下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{0m/s-v_{はじめ}}{t_{あと}-0s}\\\\{\Leftrightarrow}&&v_{はじめ}=9.8m/s^2×t_{あと} \cdots①\end{eqnarray}}\)
v-tグラフの面積から、三角形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}&&40m=\frac{1}{2}v_{はじめ}t_{あと}\\\\{\Leftrightarrow}&&t_{あと}=\frac{80m}{v_{はじめ}} \cdots②\end{eqnarray}}\)
②を①に代入して
\(\displaystyle{\begin{eqnarray}&&v_{はじめ}=9.8m/s^2×t_{あと}\\\\{\Leftrightarrow}&&v_{はじめ}=9.8m/s^2×\frac{80m}{v_{はじめ}}\\\\{\Leftrightarrow}&&v_{はじめ}^2=80×9.8m^2/s^2\\\\{\Leftrightarrow}&&v_{はじめ}^2= 8×98m^2/s^2\\\\{\Leftrightarrow}&&v_{はじめ}^2=16×49m^2/s^2\\\\{\Leftrightarrow}&&v_{はじめ}^2=4^2×7^2m^2/s^2\\\\{\Leftrightarrow}&&v_{はじめ}^2=28^2m^2/s^2\end{eqnarray}}\)
よって、
\(v_{はじめ}=28m/s\)
これを②に代入して
\(\displaystyle{\begin{eqnarray}t_{あと}&=&\frac{80m}{v_{はじめ}}\\\\&=&\frac{80m}{28m/s}\\\\&≒&2.857s\\\\&≒&2.9s\end{eqnarray}}\)
以上から
物体の初速度
\(\underline{28m/s}\)
打ち上げてから最高点に達するまでの時間
\(\underline{2.9秒}\)
3-2.問題2
\(\underline{\bf{問題2}}\)
高さ210mの建物の屋上から、物体を鉛直上向きに初速度28m/sで打ち出した。
このときの最高点に達するまでの時間、建物の屋上から最高点までの高さおよび、物体が地面に達するまでの時間を求めよ
ただし、重力加速度の大きさは\(9.8m/s^2\)とし、空気抵抗は無視できるものとする。
\(\underline{\bf{解答2}}\)
軸を設定します。
鉛直上向きに物体を発射しているので、この向きを正とします。
また、建物の屋上から最高点までの高さをh、最高点に達する時間をt、物体を発射してから地面に達するまでの時間を\(t^{\prime}\)とします。
重力加速度は\(-9.8m/s^2\)と負なので、v-tグラフは右下がりのグラフとなります。
よって、v-tグラフは下図のようになります。
最高点に到達したときを、あとの状態だと考えると
はじめ:t=0sでv=+28m/s
あと:t=tでv=0m/s
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{0m/s-(+28m/s)}{t-0s}\\\\{\Leftrightarrow}&&t=\frac{28}{9.8}\\\\{\Leftrightarrow}&&t=\frac{20}{7}\\\\{\Leftrightarrow}&&t≒2.857s\\\\{\Leftrightarrow}&&t≒2.9s\end{eqnarray}}\)
また、v-tグラフの面積から、三角形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}+h&=&\frac{1}{2}×28m/s×t\\\\&=&\frac{1}{2}×28m/s×\frac{20}{7}s\\\\&=&40m\end{eqnarray}}\)
以上から、
建物の屋上から最高点までの高さ
\(\underline{40m}\)
最高点に達する時間
\(\underline{2.9秒}\)
次に、物体を発射してから地面に達するまでの時間を求めますが、工夫してみます。
○難問→易問とするために
\(\textcolor{red}{\bf{三角形の相似を利用}}\)
v-tグラフにおける、正の面積と負の面積を形作る直角三角形について、これらは相似な図形となります。
ここで、相似な三角形の"辺の長さの比"と"面積"の関係について
\(\displaystyle{(辺の長さの比)^2=(面積の比)}\)
となるので、
\(\displaystyle{\begin{eqnarray}\left(\frac{\textcolor{red}{t^{\prime}-\frac{20}{7}}}{\textcolor{green}{\frac{20}{7}}}\right)^2=\left(\frac{\textcolor{red}{250m}}{\textcolor{green}{40m}}\right) \cdots①\end{eqnarray}}\)
ここで、上式右辺について
\(\displaystyle{\begin{eqnarray}\frac{250}{40}&=&\frac{25}{4}\\\\&=&\frac{5^2}{2^2}\\\\&=&\left(\frac{5}{2}\right)^2\end{eqnarray}}\)
これより①式の2乗の中身だけをみて
\(\displaystyle{\begin{eqnarray}&&\frac{t^{\prime}-\frac{20}{7}}{\frac{20}{7}}=\frac{5}{2}\\\\{\Leftrightarrow}&&t^{\prime}-\frac{20}{7}=\frac{5}{2}×\frac{20}{7}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{5}{2}×\frac{20}{7}+\frac{20}{7}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{20}{7}\left(\frac{5}{2}+1\right)\\\\{\Leftrightarrow}&&t^{\prime}=\frac{20}{7}×\frac{7}{2}\\\\{\Leftrightarrow}&&10s\end{eqnarray}}\)
よって、物体が地面に達するまでの時間は
\(\underline{10秒}\)
※
もちろん、負の面積部分で加速度の定義式と面積を求める式を用いても、地面に達するまでの時間を求めることができます。
地面に到達する直前の速度を\(v^{\prime}\)とすると、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-9.8m/s^2=\frac{v^{\prime}-0m/s}{t^{\prime}-t}\\\\{\Leftrightarrow}&&v^{\prime}=-9.8(t^{\prime}-t) \cdots②\end{eqnarray}}\)
面積を求める式から
\(\displaystyle{\begin{eqnarray}&&-250m=\frac{1}{2}×v^{\prime}×(t^{\prime}-t)\\\\{\Leftrightarrow}&&-500m=(t^{\prime}-t)×v^{\prime} \cdots③\end{eqnarray}}\)
②を③に代入して
\(\displaystyle{\begin{eqnarray}&&-500m=(t^{\prime}-t)×v^{\prime}\\\\{\Leftrightarrow}&&-500m=-9.8m/s^2×(t^{\prime}-t)^2\\\\{\Leftrightarrow}&&\frac{500}{9.8}s^2=(t^{\prime}-t)^2\\\\{\Leftrightarrow}&&\frac{5000}{98}s^2=(t^{\prime}-t)^2\\\\{\Leftrightarrow}&&\frac{2500}{49}s^2=(t^{\prime}-t)^2\\\\{\Leftrightarrow}&&\left(\frac{50}{7}s\right)^2=(t^{\prime}-t)^2\end{eqnarray}}\)
よって、
\(\displaystyle{\begin{eqnarray}&&t^{\prime}-t=\frac{50}{7}s\\\\{\Leftrightarrow}&&t^{\prime}=\frac{50}{7}s-t\\\\{\Leftrightarrow}&&t^{\prime}=\frac{50}{7}s-\frac{20}{7}s\\\\{\Leftrightarrow}&&t^{\prime}=\frac{70}{7}s\\\\{\Leftrightarrow}&&t^{\prime}=10s\end{eqnarray}}\)
となります。
