12.円運動と慣性力
この記事では等速円運動と慣性力について扱っています。
特に、円運動の速度と加速度については微分を用いた解説と、微分を用いていない解説を載せています。
個人的には、微分を用いた方がすっきりしているのでおすすめですが、公式的なものを覚えるのが苦痛でないならどちらの解説を参考にしてもらってもよいです。
慣性力については、これを用いる際の長所と短所などのついて載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.角速度と周期
円周上を一定の速さで動く運動を\(\textcolor{red}{\bf{等速円運動}}\)といいます。
円運動においては、直線の運動と区別するために、時間\(t[s]\)のかわりに\(\textcolor{red}{{\bf{周期}}T[s]}\)を、速度\(v[m/s]\)のかわりに\(\textcolor{red}{{\bf{角速度}}\omega[rad/s]}\)(\(\omega\)はオメガと読む)を用います。
角速度\(\omega[rad/s]\)と周期\(T[s]\)については、また詳しく説明しますが、とりあえず直線と円運動の比較を載せておきます。
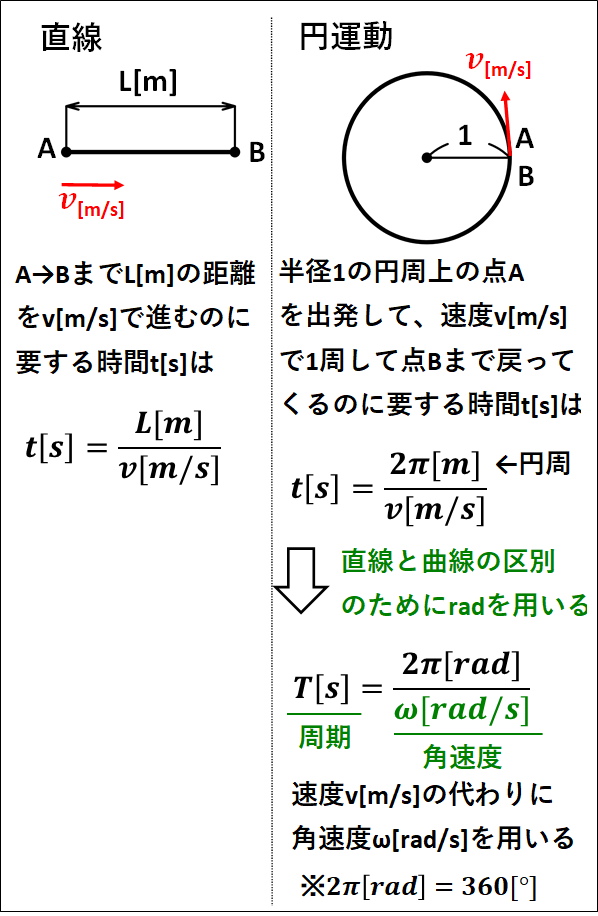
角度\(rad\)や、単位円の扱いについてはこちらも参考にしてください
→三角関数の定義と関係式
\(\underline{{\bf{○角速度}}\omega[rad/s]}\)
単位時間(1秒)あたりにどれだけの角度(\(rad\))進むかを表す量。
\(\omega[rad/s]\)は1秒間にどれだけの角度を進むかを表すので、\(t[s]\)間の間に進んだ角度は
\(\omega[rad/s]×t[s]=\omega{t}[rad]\)
となります。
これは数学の三角関数で扱う\(\theta[rad]\)の単位と同じであり、\(\omega{t}\)は角度を表すことが分かると思います。
\(\underline{{\bf{○周期}}T[s]}\)
円を1回転するのに何秒かかるかを表す量。
単位は\(s\)(秒)ですが、分かりやすくするために便宜的に\(s/(回)\)と考えると良いと思います。
また、1秒間に何回転するかを表す回転数\(n[/s]\)は、\(n[(回)/s]\)と考えると周期の逆数と単位が同じであることが分かると思います。
よって、
\(\displaystyle{\begin{eqnarray}n[/s]=\frac{1}{T[s]}\end{eqnarray}}\)
\(\displaystyle{\left(n[(回)/s]=\frac{1}{T[s/(回)]}\right)}\)
上記のように、1回転するのに何秒かかるかの逆数をとると、1秒間に何回転するかになります。
また、単位\([/s]\)は\([Hz]\)(ヘルツ)とも書きます。
2.等速円運動とベクトル図(微分有り)
半径\(r\)の円周上の点\(A\)を出発して\(t[s]\)後の点\(P\)を考えます。
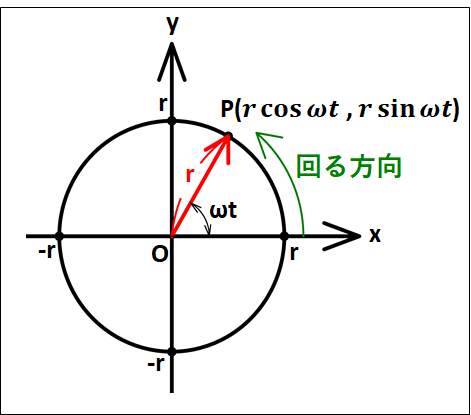
ここで、\(\overrightarrow{OP}\)を成分表示すると、次のようになります。
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}r\cos\omega{t}\\r\sin\omega{t}\end{array}\right)}\)
※円周上の点と、ベクトルの成分表示についてはこちら
→三角関数の定義と関係式
→力とベクトル
\(\overrightarrow{OP}\)の大きさを考えると、
\(\displaystyle{\begin{eqnarray}|\overrightarrow{OP}|&=&\sqrt{(r\cos\omega{t})^2+(r\sin\omega{t})^2}\\\\&=&\sqrt{r^2(\cos^2\omega{t}+\sin^2\omega{t})}\\\\&=&\sqrt{r^2}\\\\&=&r\end{eqnarray}}\)
となります。
これは図からも、\(\overrightarrow{OP}\)の長さと、単位円上の点\(P\)と原点\(O\)を結ぶ線分の長さがともに半径\(r\)であることから分かります。
次に速度と加速度、またその大きさを考えていきます。
速度は位置を時間\(t\)で微分したもの、加速度は速度を時間\(t\)で微分したものでした。
→変位・速度・加速度
実際に位置ベクトル\(\overrightarrow{OP}\)の成分を、それぞれ\(t\)で微分します。
等速円運動では、\(r\)と\(\omega\)が一定であることに注意してください。(定数として扱う)
\(\cos\omega{t}\)について、\(\omega{t}=u\)とおくと
\(\displaystyle{\begin{eqnarray}&&\frac{d}{dt}\cos\omega{t}\\\\=&&\frac{d}{du}\cos{u}\frac{du}{dt}\\\\=&&\frac{d}{du}\cos{u}\frac{d}{dt}\omega{t}\\\\=&&-\sin{u}・\omega\\\\=&&-\omega\sin\omega{t}\end{eqnarray}}\)
※合成関数の微分を用いた
→微分法とその応用

よって、\(x\)成分の速度は\(x=r\cos\omega{t}\)とおくと
\(\displaystyle{\begin{eqnarray}v_x&=&\frac{dx}{dt}\\\\&=&\frac{d}{dt}r\cos\omega{t}\\\\&=&r\frac{d}{dt}\cos\omega{t}\\\\&=&-r\omega\sin\omega{t}\end{eqnarray}}\)
となります。
同様にして、\(y\)成分\(y=r\sin\omega{t}\)も\(t\)で微分すると
\(\displaystyle{\begin{eqnarray}v_y&=&\frac{dy}{dt}\\\\&=&\frac{d}{dt}r\sin\omega{t}\\\\&=&r\omega\cos\omega{t}\end{eqnarray}}\)
以上から、
\(\displaystyle{\begin{eqnarray}\vec{v}&=&\left(\begin{array}{c}v_x\\v_y\end{array}\right)\\\\&=&\left(\begin{array}{c}-r\omega\sin\omega{t}\\r\omega\cos\omega{t}\end{array}\right)\end{eqnarray}}\)
大きさを考えると、
\(\displaystyle{\begin{eqnarray}|\vec{v}|&=&\sqrt{v_x^2+v_y^2}\\\\&=&\sqrt{(-r\omega\sin\omega{t})^2+(r\omega\cos\omega{t})^2}\\\\&=&\sqrt{r^2{\omega}^2}\\\\&=&r\omega\end{eqnarray}}\)
ふつうは、\(|\vec{v}|\)を単に\(v\)と書きます。
加速度も同様にして、速度の成分を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a_x&=&\frac{dv_x}{dt}\\\\&=&\frac{d}{dt}(-r\omega\sin\omega{t})\\\\&=&-r{\omega}^2\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a_y&=&\frac{dv_y}{dt}\\\\&=&\frac{d}{dt}(r\omega\cos\omega{t})\\\\&=&-r{\omega}^2\sin\omega{t}\end{eqnarray}}\)
以上から、
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\left(\begin{array}{c}a_x\\a_y\end{array}\right)\\\\&=&\left(\begin{array}{c}-r{\omega}^2\cos\omega{t}\\-r{\omega}^2\sin\omega{t}\end{array}\right)\end{eqnarray}}\)
大きさは、
\(\displaystyle{\begin{eqnarray}|\vec{a}|&=&\sqrt{a_x^2+a_y^2}\\\\&=&\sqrt{(-r{\omega}^2\cos\omega{t})^2+(-r{\omega}^2\sin\omega{t})^2}\\\\&=&\sqrt{r^2{\omega}^4}\\\\&=&r{\omega}^2\\\\&=&r\left(\frac{v}{r}\right)^2\\\\&=&\frac{v^2}{r}\end{eqnarray}}\)
ふつうは、\(|\vec{a}|\)を単に\(a\)と書きます。
上式の、\(r{\omega}^2\)について、速度の大きさの部分で見たように
\(\displaystyle{\begin{eqnarray}v=r\omega {\Leftrightarrow} \omega=\frac{v}{r}\end{eqnarray}}\)
なので、これを\(a=r{\omega}^2\)に代入して
\(\displaystyle{\begin{eqnarray}a&=&r{\omega}^2\\\\&=&\frac{v^2}{r}\end{eqnarray}}\)
となります。
以上のことをまとめておきます。
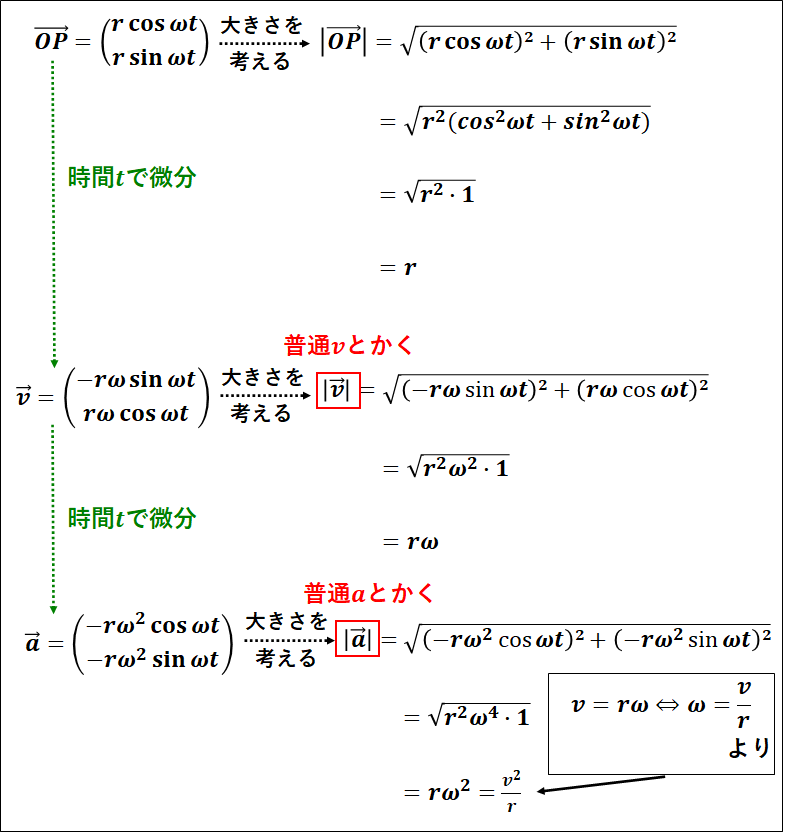
次に、この位置と速度と加速度のベクトルの向きをみていきます。
\(\underline{\bf{○位置ベクトル}}\)
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}r\cos\omega{t}\\r\sin\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の正の方向に1進んで、\(y\)軸の正の方向に1進む向きです。
\(\underline{\bf{○速度ベクトル}}\)
\(\displaystyle{\vec{v}=\left(\begin{array}{c}-r\omega\sin\omega{t}\\r\omega\cos\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r\omega=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\vec{v}=\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の負の方向に1進んで、\(y\)軸の正の方向に1進む向きです。
\(\underline{\bf{○加速度ベクトル}}\)
\(\displaystyle{\vec{a}=\left(\begin{array}{c}-r{\omega}^2\cos\omega{t}\\-r{\omega}^2\sin\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r{\omega}^2=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\vec{a}=\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の負の方向に1進んで、\(y\)軸の負の方向に1進む向きです。
上記の速度と加速度のベクトルの向きを、点Pを始点として描くと下図のようになります。
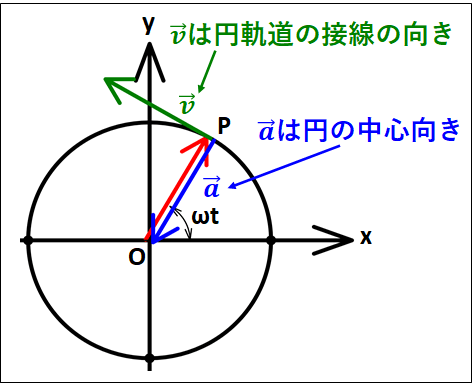
3.等速円運動の速度と加速度(微分無し)
先ほどの内容を、微分を用いずにみていきます。
\(\underline{\bf{○速度の大きさ}}\)
速さは、
\(\displaystyle{\bf{速さ=\frac{距離}{時間}}}\)
となります。
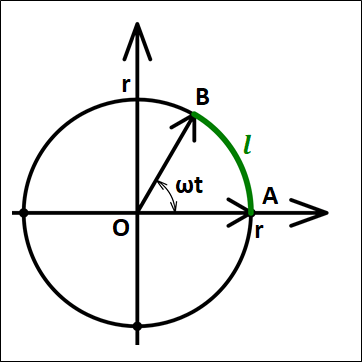
上図は、点\(A\)にいた物体が、\(t\)秒後に半径\(r\)の円周に沿って点\(B\)に移動した様子を表した図になります。
ここで、点が動いた距離は弧\(AB\)、すなわち図中の\(\textcolor{green}{l}\)となります。
この\(\textcolor{green}{l}\)は、角度が\(2\pi(=360°)\)に対して、\(\omega{t}\)分の円周(\(2\pi{r}\))になるので、
\(\displaystyle{\begin{eqnarray}\textcolor{green}{l}&=&2\pi{r}×\frac{\omega{t}}{2\pi}\\\\&=&r\omega{t}\end{eqnarray}}\)
これより速さは、距離を時間で割って、
\(\displaystyle{\begin{eqnarray}v&=&\frac{\textcolor{green}{l}}{t}\\\\&=&\frac{r\omega{t}}{t}\\\\&=&r\omega\end{eqnarray}}\)
となります。
\(\underline{\bf{○速度の向き}}\)
速度の定義は
\(\displaystyle{\vec{v}=\lim_{\Delta{t}\to0}\frac{\vec{r_{あと}}-\vec{r_{はじめ}}}{\Delta{t}}}\)
となります。
→変位・速度・加速度
よって、速度の大きさで見た図において、
\(\displaystyle{\vec{r_{はじめ}}=\overrightarrow{OA}}\)
\(\vec{r_{あと}}=\overrightarrow{OB}\)
となります。
そうすると、
\(\vec{r_{あと}}-\vec{r_{はじめ}}=\overrightarrow{AB}\)
となります。
→ベクトルの演算と成分表示
そして\(\Delta{t}\to0\)、すなわち\(\omega{t}\)という角度を限りなく\(0\)に近づけていくと、点\(A\)における速度ベクトルは点\(A\)における円の接線方向であることがわかります。
※
今
\(t_{はじめ}=0\)
\(t_{あと}=t\)
なので、
\(\Delta{t}=t-0=t\)
よって、\(\Delta{t}\to0\)と\(t\to0\)はおなじことを指している。
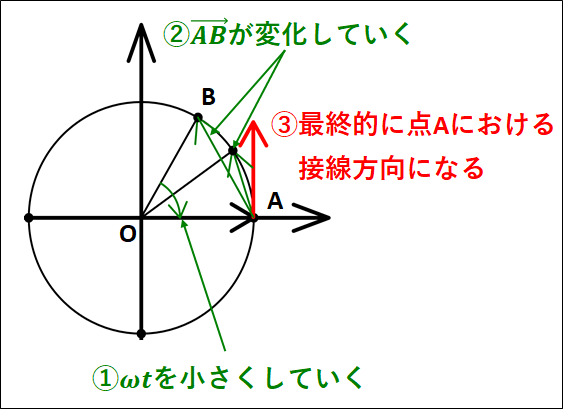
以上から、円運動の速度について
大きさ:\(r\omega\)
向き:接線方向
となります。
\(\underline{\bf{○加速度の大きさ}}\)
加速度の定義は
\(\displaystyle{\vec{a}=\lim_{\Delta{t}\to0}\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}}\)
となります。
また、速度ベクトルは円の接線方向でした。
よって、下図のようなベクトルを考えます。
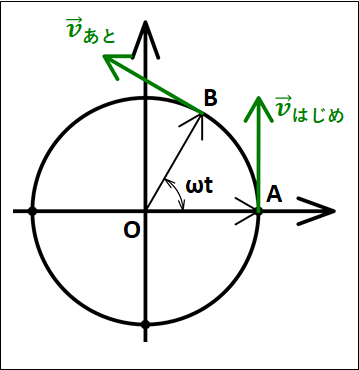
点\(A\)がはじめの位置、点\(B\)はあとの位置になります。
また、それぞれの位置における速度を\(\vec{v_{はじめ}}\)、\(\vec{v_{あと}}\)としています。
ベクトルは平行移動させてもよいので、速度ベクトルの始点を一致させてみます。
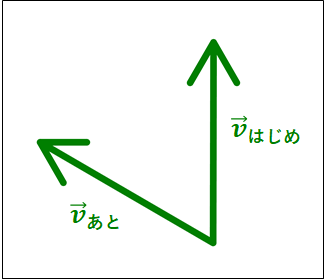
これらのなす角を求めるために、次の図を考えます。
図は円と速度ベクトルの始点を一致させた図を一緒に載せたものです。
また、\(\vec{v_{あと}}\)は見やすいように途中で切ってあります。
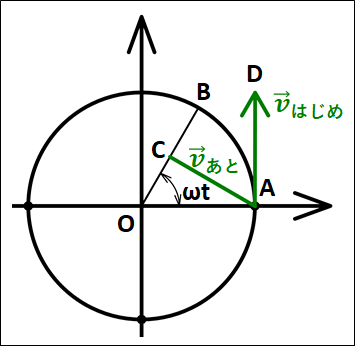
解説では、角度の単位\([rad]\)と\([°]\)が混じっています。
気になる方は、\(90°\)を\(\frac{\pi}{2}\)として考えてください。
点\(C\)は、\(OB\)と\(\vec{v_{あと}}\)との交点で、点\(D\)は\(\vec{v_{はじめ}}\)の始点です。
図から
\(\angle{B OA}=\omega{t}\)
となっています。
また、点\(B\)における速度が\(\vec{v_{あと}}\)であり、\(\vec{v_{あと}}\)は円の接線方向なので、\(OB\)と\(AC\)は直角です。
これより
\(\angle{OCA}=90°\)
よって、残った\(\angle{OAC}\)は\((90°-\omega{t})\)であると分かります。
次に、\(\vec{v_{はじめ}}\)は点\(A\)における接線方向なので
\(\angle{OA D}=90°\)
であり、また図から
\(\angle{O AD}=\angle{O AC}+\angle{C AD}\)
となります。
以上のことから、
\(\angle{O AD}=\angle{O AC}+\angle{C AD}\)
に
\(\angle{O AC}=(90°-\omega{t})\)
と
\(\angle{O AD}=90°\)
を代入して整理すると、
\(\displaystyle{\begin{eqnarray}&&\angle{O AD}=\angle{O AC}+\angle{C AD}\\\\{\Leftrightarrow}&&90°=90°-\omega{t}+\angle{C AD}\\\\{\Leftrightarrow}&&\angle{C AD}=\omega{t}\end{eqnarray}}\)
\(\angle{CAD}\)は\(\vec{v}_{はじめ}\)と\(\vec{v}_{あと}\)のなす角です。
よって、はじめとあとの速度ベクトルがなす角が\(\omega{t}\)であることが分かりました。
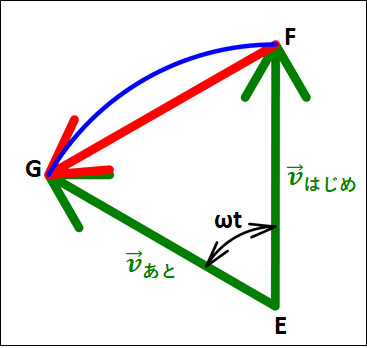
上図から、加速度の定義における\(\vec{v_{あと}}-\vec{v_{はじめ}}\)は赤色の\(\overrightarrow{FG}\)となります。
ここで、速度ベクトルの大きさは\(r\omega\)なので、速度の大きさを考えたときと同様に半径が\(r\omega\)の円における弧\(FG\)を考えると、
\(\displaystyle{\begin{eqnarray}\stackrel{\Large \frown}{FG}&=&2r\omega\pi×\frac{\omega{t}}{2\pi}\\\\&=&r{\omega}^2t\end{eqnarray}}\)
ここで、\(\Delta{t}\to0\)とすると弧\(FG\)と線分\(FG\)は限りなく等しくなってきます。
(長さの差が限りなく小さくなっていく)
これより、
\(\displaystyle{\begin{eqnarray}\Delta{v}&=&|\vec{v_{あと}}-\vec{v_{はじめ}}|\\\\&=&FG\\\\&≒&\stackrel{\Large \frown}{FG}\\\\&=&r{\omega}^2t\end{eqnarray}}\)
よって、加速度の大きさは
\(\displaystyle{\begin{eqnarray}|\vec{a}|&=&\frac{\Delta{v}}{\Delta{t}}\\\\&=&\frac{r{\omega}^2t}{t}\\\\&=&r{\omega}^2\end{eqnarray}}\)
また、速度の大きさ\(v=r\omega\)を用いると
\(\displaystyle{|\vec{a}|=r{\omega}^2=\frac{v^2}{r}}\)
となります。
\(\underline{\bf{○加速度の向き}}\)
\(\vec{a}\)の向きは\(\vec{v_{あと}}-\vec{v_{はじめ}}\)において\(\Delta{t}\)を限りなく\(0\)に近づけた際のベクトルの向きになります。
また、先ほどの図において、\(\vec{v_{あと}}-\vec{v_{はじめ}}\)は\(\vec{FG}\)となります。
よって、\(\omega{t}\)を限りなく\(0\)に近づけていくと、\(\vec{FG}\)は\(\vec{v_{はじめ}}\)と直角をなす向きになることが分かると思います。
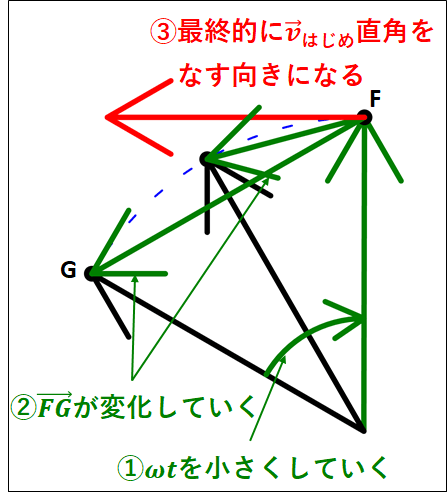
この\(\vec{a}\)を円の点\(A\)が始点になるように図示すると、下図のようになります。
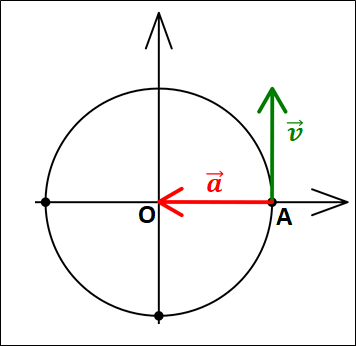
図から、\(\vec{a}\)は円の中心に向かう向きであることが分かります。
以上から、円運動の加速度について
大きさ:
\(\displaystyle{r{\omega}^2=\frac{v^2}{r}}\)
向き:円の中心方向
となります。
4.向心力
等速円運動をしている物体は、円の中心方向を正とした力を受けます。
この力を\(\textcolor{red}{\bf{向心力}}\)といいます。
等速円運動をしている物体について考える際には、向心力を見つけて運動方程式を立てることが重要となってきます。
※等速円運動をしている物体の加速度が円の中心向きだったので、運動方程式右辺の力も円の中心に向かう力(向心力)を正として立てる
5.慣性力と遠心力
\(\textcolor{red}{\bf{慣性力}}\)とは、"加速度運動をしている人(物体)が感じる\(\textcolor{red}{\bf{仮想的}}\)な力"のことです。
仮想的な力であるので、本来存在せず、作用・反作用の関係はありません。
\(\underline{\bf{○慣性力を用いる際の長所と短所}}\)

\(\bf{<証明>}\)
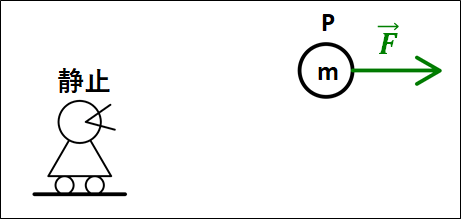
(静止している人から見た\(P\)の)運動方程式は
\(\displaystyle{m\vec{a}_{静止\to{P}}=\vec{F}}\)
この加速度ベクトルを下図のように分解します。
ベクトルの分解についてはこちら
→ベクトルの演算と成分表示
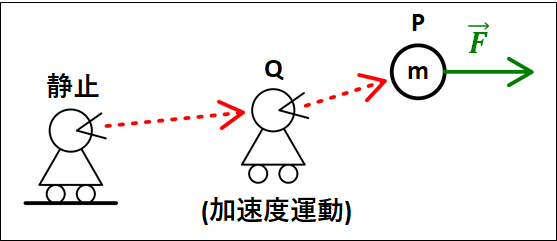
運動方程式は、
\(\displaystyle{m(\vec{a}_{静止\to{Q}}+\vec{a}_{Q\to{P}})=\vec{F}}\)
上式の\(m\vec{a}_{静止\to{Q}}\)を右辺に移項すると"(加速度運動している\(Q\)から見た\(P\)の)運動方程式"となります。
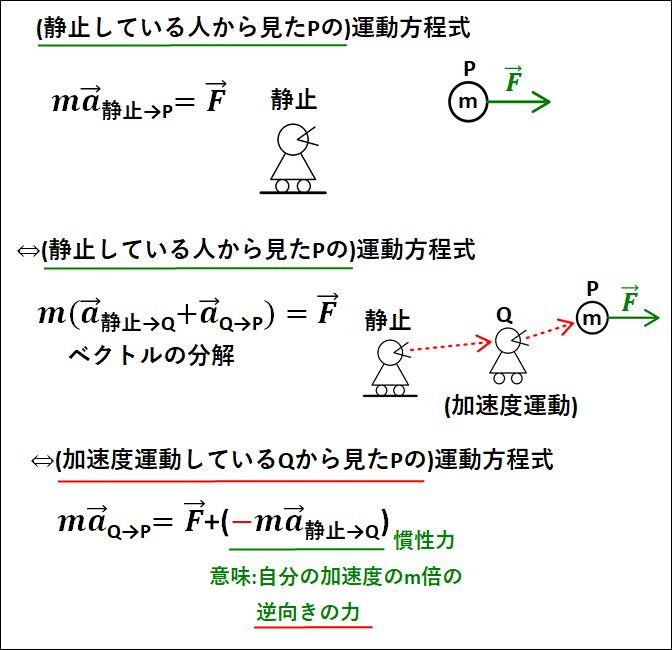
\(\displaystyle{m\vec{a}_{Q\to{P}}=\vec{F}-m\vec{a}_{静止\to{Q}}}\)
上式の\(-m\vec{a}_{静止\to{Q}}\)が慣性力となり、"自分(静止した人からみた加速度運動している人)の加速度の\(m\)倍で逆向きの力"となります。
下図にまとめておきます。
\(\underline{\bf{○遠心力}}\)
遠心力も慣性力です。
これは、円運動している物体と同じ円運動をしている人から見た慣性力となります。
遠心力は、円の中心から外向きにはたらきます。
遠心力も慣性力なのでみかけ上の(仮想的な)力となります。
6.円運動の式まとめ
○角速度\(\omega[rad/s]\)
→単位時間(1秒)あたり、何\(rad\)回転するか
\(t\)秒間では\(\omega{t}[rad]\)回転する。
この単位は、三角関数で扱う角度\(\theta\)と同じ単位。
○周期\(T[s]\)
→1回転するのに何秒かかるか
単位は便宜的に\(T[s/(回)]\)と考えるとわかりやすい。
\(\displaystyle{\bf{周期=\frac{円周}{速さ}}}\)
半径\(r\)の円の場合
\(\displaystyle{T[s]=\frac{2\pi{r}}{v}\left(=\frac{2\pi}{\omega}\right)}\)
(※\(v=r\omega\)を用いた)
周期の逆数\(n[/s]\) \((n[(回)/s])\) は、1秒間に何回転するかを表す。
\(\displaystyle{n[(回)/s]=\frac{1}{T[s/(回)]}}\)
また、単位[/s]は[Hz](ヘルツ)とも書く
※便宜的に単位に(回)をつけているだけで、実際の単位に(回)はつけない。
○円運動の速度の大きさと向き
・速度の大きさと角速度の関係
→\(v=r\omega\)
・速度の向き
→円の接線方向
○円運動の加速度の大きさと向き
・加速度の大きさ
\(\displaystyle{a=r{\omega}^2=\frac{v^2}{r}}\)
・加速度の向き
→円の中心方向
個人的に、角速度は問題文で単位と共に記載があると思うので、単位の意味がわかっていれば覚える必要は無いと思います。
周期と回転数については、意味を把握し、単位に(回)を補ってやるとわかりやすいです。
速度と加速度については、円周上の点を成分で表すことさえわかっていれば、あとは成分の微分とベクトルの大きさを計算すれば求めることができます。
慣れればそこまで時間はかからないですし、うろ覚えであった際の確認にも使えます。
