14.万有引力
この記事では、ケプラーの法則や万有引力がどのように表されるか、また万有引力による位置エネルギーについて解説しています。
第1宇宙速度や第2宇宙速度についても触れていますが、詳しくは練習問題で扱っています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
→万有引力
Twitterアカウント→@roke_blog
目次
1.ケプラーの法則
\(\textcolor{red}{\bf{ケ プラーの法則}}\)とは、ケプラーによって発見された惑星の運動に関する法則のこととなります。
第1法則から第3法則まであるので、これらについてみていきます。
\(\underline{\bf{○第1法則}}\)
惑星は、太陽を1つの焦点とする楕円軌道を描く。
これは、説明のとおり惑星は太陽を1つの焦点とする楕円軌道で太陽の周りを回りますよというものです。
\(\underline{\bf{○第2法則}}\)
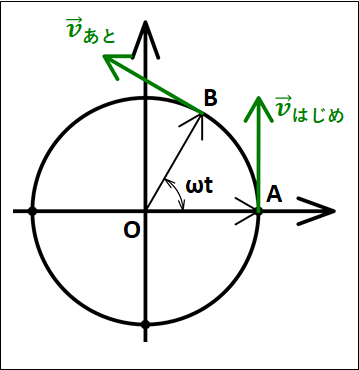
惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である。
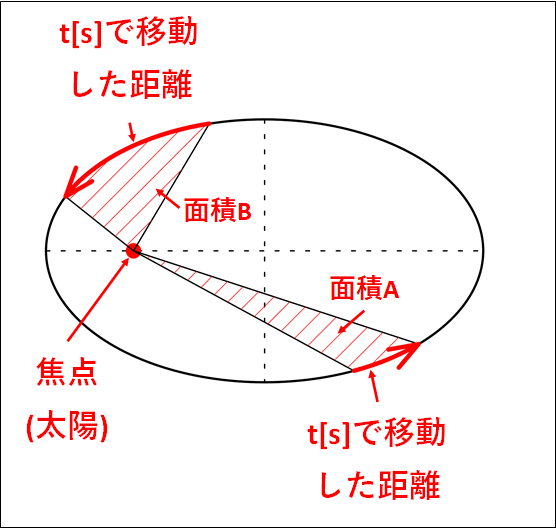
上図において、2つの赤い矢印は、\(t[s]\)の間に惑星が楕円軌道上を動いた距離となります。
このとき、惑星と焦点(太陽)を結ぶ線分が一定時間に描く面積は、それぞれ\(\textcolor{red}{A , B}\)となります。
第2法則は、この面積について
\(\textcolor{red}{\bf{面積A=面積B}}\)
になりますよ、というものです。
また、第2法則は
\(\textcolor{red}{\bf{面積速度一定の 法則}}\)
ともいいます。
先ほど見た図では\(t[s]\)で描く面積が\(A\)や\(B\)でしたが、面積速度とは、\(t[s]\)ではなく単位時間(1秒)で描く面積のこととなります。
特に、下図のような状況を考えます。
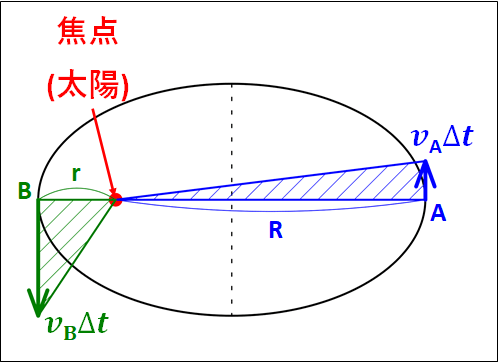
微小時間\(\Delta{t}\)の間に、点Aと点Bにおける速度がそれぞれ\(\textcolor{blue}{v_A}\)と\(\textcolor{green}{v_B}\)である物体が進む距離はそれぞれ\(\textcolor{blue}{v_A\Delta{t}}\)と\(\textcolor{green}{v_B\Delta{t}}\)となります。
微小時間なので、図のように点A、Bにおける楕円の接線の向きに進んだと近似してあります。
また、焦点(太陽)から点A、Bそれぞれまでの距離を\(\textcolor{blue}{R}\)、\(\textcolor{green}{r}\)としています。
このとき、青色の斜線部分面積を\(\textcolor{blue}{\Delta{S_A}}\)、緑色の斜線部分面積を\(\textcolor{green}{\Delta{S_B}}\)とすると、三角形の面積の式から
\(\displaystyle{\textcolor{blue}{\Delta{S_A}=\frac{1}{2}Rv_A\Delta{t}}}\)
\(\displaystyle{\textcolor{green}{\Delta{S_B}=\frac{1}{2}rv_B\Delta{t}}}\)
このとき、微小時間\(\Delta{t}\)の間に描いた面積は等しいので
\(\displaystyle{\begin{eqnarray}&&\textcolor{blue}{\Delta{S_A}}=\textcolor{green}{\Delta{S_B}}\\\\{\Leftrightarrow}&&\textcolor{blue}{\frac{1}{2}Rv_A\Delta{t}}=\textcolor{green}{\frac{1}{2}rv_B\Delta{t}}\end{eqnarray}}\)
この面積を微小時間で割ったものが面積速度なので、両辺微小時間\(\Delta{t}\)で割って
\(\displaystyle{\textcolor{blue}{\frac{1}{2}Rv_A}=\textcolor{green}{\frac{1}{2}rv_B}}\)
上式は面積速度(単位時間あたりに描く面積)が等しいことを表しています。
また、上図の点Aは太陽から最も遠ざかる点であり、この点を\(\textcolor{blue}{\bf{遠日点}}\)といいます。
点Bは太陽に最も近づく点であり、この点を\(\textcolor{red}{\bf{近日点}}\)といいます。
同じ時間に移動した点が描く面積が一定となることから、太陽の周りを楕円軌道で運動する惑星の速さは、\(\textcolor{blue}{\bf{遠日点}}\)で最小、\(\textcolor{red}{\bf{近日点}}\)で最大となります。
ちなみに、一般の位置における面積速度を考えてみます。
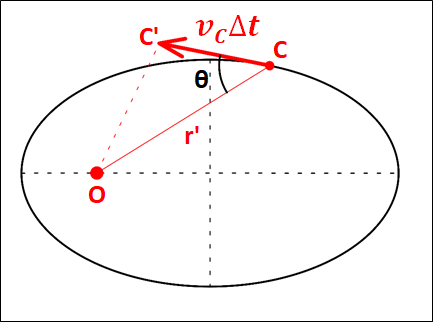
こちらも先ほどと同様にして、点Cにおける速度を\(v_C\)、微小時間\(\Delta{t}\)の間に進んだ距離は、点Cにおける楕円の接線方向に\(v_C\Delta{t}\)となります。
また、\(OC=r^{\prime}\)とし、速度の方向と\(OC\)のなす角を\(\theta\)とします。
このとき、三角形\(OCC^{\prime}\)に注目します。
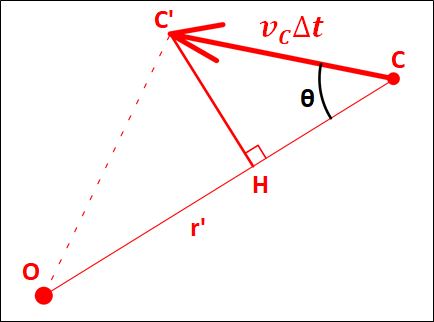
\(C^{\prime}\)から線分\(OC\)に垂直な線分\(C^{\prime}H\)を引きます。
そうすると、\(CC^{\prime}H\)は\(CC^{\prime}\)を斜辺とする直角三角形となるので、三角関数から
\(\displaystyle{\begin{eqnarray}C^{\prime}H&=&CC^{\prime}×\sin\theta\\\\&=&v_C\Delta{t}\sin\theta\end{eqnarray}}\)
※三角関数についてはこちら
→三角関数の定義と関係式
以上から、三角形\(OCC^{\prime}\)は、
底辺:
\(OC=r^{\prime}\)
高さ:
\(C^{\prime}H=v_C\Delta{t}\sin\theta\)
の三角形なので、この三角形の面積は、
\(\displaystyle{\frac{1}{2}r^{\prime}v_C\Delta{t}\sin\theta}\)
よって、面積速度は\(\Delta{t}\)で割って
\(\displaystyle{\frac{1}{2}r^{\prime}v_C\sin\theta}\)
となります。
\(\underline{\bf{○第3法則}}\)
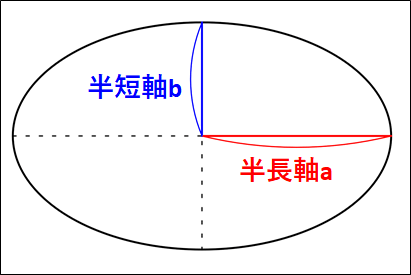
惑星の公転周期\(T\)の2乗は、楕円軌道の半長軸\(a\)の3乗に比例する。
半長軸とは、楕円における長い方の直径の半分の長さのことです。
ちなみに、短い方の直径を短軸といいます。
また、上記の事柄を式で表すと、比例定数を\(k\)として
\(\displaystyle{T^2=ka^3}\)
となります。
上式を変形すると
\(\displaystyle{\begin{eqnarray}&&T^2=ka^3\\\\{\Leftrightarrow}&&\frac{T^2}{a^3}=k (一定)\end{eqnarray}}\)
となります。
このことから、1つめの惑星の周期を\(T_1\)、楕円軌道の半長軸を\(a_1\)とし、同様にして2つめ、3つめ…の惑星についても\(T_2,T_3,\cdots\)、\(a_2,a_3,\cdots\)とします。
これらの惑星について、
\(\displaystyle{\frac{T^2}{a^3}}\)
は一定となるので
\(\displaystyle{\frac{T_1^2}{a_1^3}=\frac{T_2^2}{a_2^3}=\frac{T_3^2}{a_3^3}=\cdots}\)
が成り立ちます。
第3法則については、練習問題でも扱っています。
2.万有引力の法則
\(\textcolor{red}{\bf{万有 引力}}\)は、質量をもつ物体間にはたらく力で、お互いに引きつける向きにはたらきます。
2物体間にはたらく万有引力の大きさ\(F[N]\)は、2物体の質量をそれぞれ\(m_1,m_2\)とすると、この質量の積に比例し物体間の距離\(r[m]\)の2乗に反比例します。
物体間の距離\(r[m]\)は中心間の距離を用います。
また。万有引力は\(\textcolor{red}{\bf{保存力}}\)となります。
※保存力と非保存力についてはこちら
→仕事とエネルギー
なので、仕事とエネルギーの等価性原理から、万有引力がした仕事を左辺のエネルギー項に移項すると、万有引力による位置エネルギーの変化量になります。
万有引力の大きさ\(F\)を式で表すと、比例定数\(G\)を用いて、
\(\displaystyle{F=G\frac{m_1m_2}{r^2}}\)
となります。
この比例定数\(G\)を\(\textcolor{green}{\bf{万有 引力定数}}\)といいます。
単位は、
\(\displaystyle{F[N]=G\frac{m_1[kg]m_2[kg]}{r^2[m^2]}}\)
から
\(\displaystyle{G=F[N]×\frac{r^2[m^2]}{m_1m_2[kg^2]}}\)
となるので、\([N・m^2/kg^2]\)となります。
※未知の単位を求める次元解析についてはこちら
→単位の計算・換算練習問題2(次元解析と解答確認)
練習問題では、万有引力の法則を用いてケプラーの第3法則を求めています。
3.万有引力と重力
地球上の物体にはたらく重力は、物体と地球との間にはたらく万有引力と、地球の自転による遠心力との合力となります。
ですが、地球の自転による遠心力は、万有引力に比べてとても小さいので無視できます。
よって、"地球上の物体にはたらく重力は、地球と物体の間の万有引力であると考えてよい"です。
地球と物体の質量をそれぞれ\(M,m\)とし、地球の半径を\(R\)地上での重力加速度を\(g\)とすると、\(\textcolor{red}{\bf{地表において}}\)
\(\displaystyle{\begin{eqnarray}&&mg=G\frac{Mm}{R^2}\\\\{\Leftrightarrow}&&g=G\frac{M}{R^2}\end{eqnarray}}\)
となります。
4.第1宇宙速度
\(\textcolor{red}{\bf{第1宇宙 速度}}\)とは、人工衛星が地表近くを円運動する速さのことです。
詳しくは練習問題で扱いますが、人工衛星が地表近くを等速円運動するとして求めます。
5.万有引力による位置エネルギー
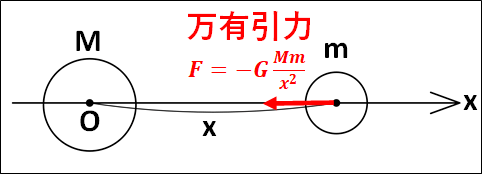
上図は、距離が\(x\)だけはなれた質量\(M\)と\(m\)の物体について考えたものです。
質量\(m\)の物体には万有引力が、質量\(M\)の物体に引き付けられる向きにはたらいています。
万有引力の大きさは、
\(\displaystyle{F=G\frac{Mm}{x^2}}\)
から、\(x\)が大きくなるほど、つまり物体同士が離れるほど小さくなり、十分に遠方だとほとんど\(0\)となります。
万有引力による位置エネルギーの基準は、万有引力が\(0\)となるような十分に遠方の点である無限遠点とすることが多いです。
図の状態において、質量\(m\)の物体の運動方程式は
\(\displaystyle{ma=-G\frac{Mm}{x^2}}\)
これを\(\textcolor{green}{\bf{エネルギー積 分}}\)していきます。
※エネルギー積分についてはこちらの記事の、「4.運動エネルギーと仕事の関係」も参考にしてください。
→仕事とエネルギー
先ほどの運動方程式の両辺に\(v\)を掛けて
\(\displaystyle{m\textcolor{red}{v}a=-G\frac{Mm}{x^2}\textcolor{red}{v}}\)
速度と加速度の定義式
\(\displaystyle{v=\frac{dx}{dt} , a=\frac{dv}{dt}}\)
から、運動方程式は
\(\displaystyle{\begin{eqnarray}&&m\textcolor{red}{v}a=-G\frac{Mm}{x^2}\textcolor{red}{v}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=-G\frac{Mm}{x^2}\frac{dx}{dt}\end{eqnarray}}\)
※変位・速度・加速度についてはこちら
→変位・速度・加速度
ここで、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left\{\frac{1}{2}mv^2\right\}&=&\frac{dv}{dt}\frac{d}{dv}\left\{\frac{1}{2}mv^2\right\}\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left\{G\frac{Mm}{x}\right\}&=&\frac{dx}{dt}\frac{d}{dx}\left\{G\frac{Mm}{x}\right\}\\\\&=&-G\frac{Mm}{x^2}\frac{dx}{dt}\end{eqnarray}}\)
となるので、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}=-G\frac{Mm}{x^2}\frac{dx}{dt}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2\right\}=\frac{d}{dt}\left\{G\frac{Mm}{x}\right\}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2+\left(-G\frac{Mm}{x}\right)\right\}=0\end{eqnarray}}\)
※\(x^{-2}\)の微積についてはこちら
→微分法とその応用
→積分法の応用
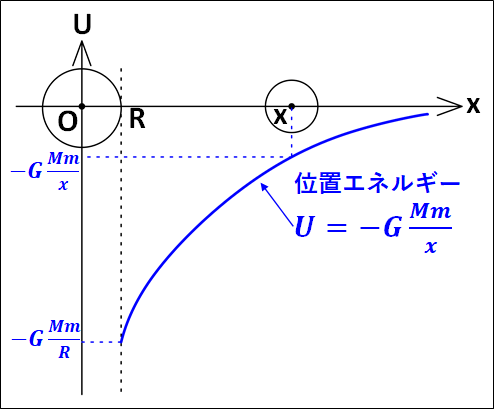
上記から、万有引力による位置エネルギー\(U\)は
\(\displaystyle{\textcolor{green}{U=-G\frac{Mm}{x}}}\)
で表され、さらに力学的エネルギーは保存することが分かります。

また、中心間距離\(x\)と万有引力による位置エネルギー\(U\)の関係を表したグラフは下図のようになります。
6.第2宇宙速度
\(\textcolor{red}{\bf{第2宇宙 速度}}\)とは、物体が地球の重力(万有引力)を振り切って、どこまでも遠くに飛んでいくように投げる際に必要な最低限の速度のことです。
こちらも詳しくは、練習問題で扱っています。
13.単振動
この記事では単振動を扱っています。
単振動は、等速円運動の正射影となります。
単振動に関する運動方程式の解き方や、一般解、単振動のエネルギーについても解説しています。
また、水平ばね振り子や鉛直ばね振り子の紹介もしています。
鉛直ばね振り子では、つりあいの位置を原点にしたものと、自然長の位置を原点にしたものの2通りをみています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
→単振動
Twitterアカウント→@roke_blog
目次
1.単振動とは
\(\textcolor{red}{\bf{単振動}}\)とは、
①等速円運動の正射影と同じ運動であり
②運動方程式が
\(ma=-k(x-x_0)\)
の形
のものとなります。
上記の①、②についてみていきます。
円運動についてはこちら
→円運動と慣性力
\(\underline{\bf{①等速円運動の正射影}}\)
次のように、半径(A)の円周上を①→②→③→④→①と移動する物体を考えます。
この物体をある一方向からみたものが正射影となります。
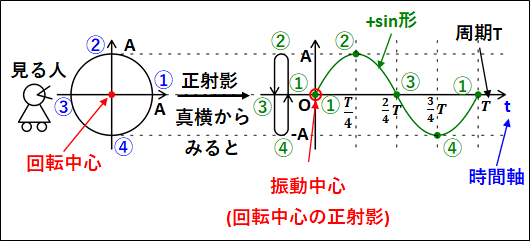
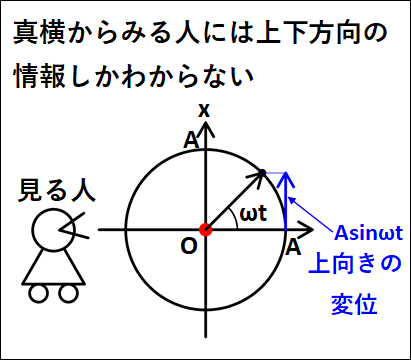
真横からみているので、奥行き方向(図中での左右方向)の動きは分からず、上下方向の動きのみをみています。
この上下方向の動きと、時間の関係を表したグラフが図中右側のグラフとなっています。
これは、三角関数のグラフと同じ形になっています。
※三角関数のグラフについてはこちら
→三角関数のグラフ
また、上記では真横からみましたが、真上からみると次のようになります。
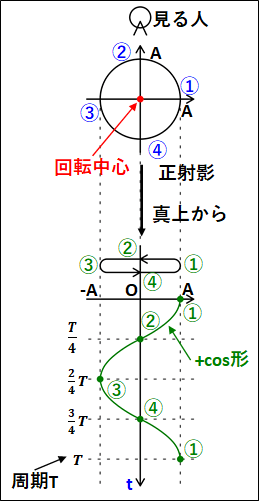
こちらに関しても真上から見ているので、みている人からは図中の上下方向の動きはわからず、左右方向の動きしかわかりません。
左右方向の動きと、時間の関係を表したグラフが図中の下のグラフになります。
上記の円の半径\(A[m]\)を\(\textcolor{red}{\bf{振幅}}\)といいます。
振幅は、振動中心からの変位の最大値となります。
(振動中心から最も離れたとき、中心からの距離が\(A[m]\)となる)
また、単振動は等速円運動の正射影と同じ運動であるといいましたが、用いる量もだいたいおなじとなります。
ただし、名称が多少変わっているものもあります。
・角振動数:\(\omega[rad/s]\)
(等速円運動では、角速度と呼んでいた)
こちらも、扱いは変わらず単位時間あたりに進む角度を表しています。
\(t\)秒間で進む角度は等速円運動のときと同様に\(\omega{t}[rad]\)となります。
・位相:\(\omega{t}[rad]\)
こちらは、等速円運動においては時刻\(t\)のときの回転角を表していました。
単振動では、時刻\(t\)における物体の状態を表します。
・周期:\(T[s]\)
単振動における周期\(T[s]\)は、物体が一回往復する時間となります。
(等速円運動とおなじく、\(T[s/(回)]\)と考えると良い)
また、こちらも等速円運動における回転数と同様に、逆数は1秒間に何回振動するかを表し、これを"振動数\(f[Hz]\)"といいます。
(\(Hz=/s , f[(回)/s]\)と考えるとよい)
\(\displaystyle{f[Hz]=\frac{1}{T[s]}}\)
\(\displaystyle{\left(f[(回)/s]=\frac{1}{T[s/(回)]}\right)}\)
また、
\(\displaystyle{\begin{eqnarray}&&T=\frac{2\pi}{\omega}\\\\{\Leftrightarrow}&&\omega=\frac{2\pi}{T}\end{eqnarray}}\)
となります。
上記の周期と振動数の関係を用いると
\(\displaystyle{\omega=\frac{2\pi}{T}=2{\pi}f}\)
と表すこともできます。
※周期について
後ほど詳しく説明しますが…
上記の真横からみた正射影について、回転する円を次のように設定します。
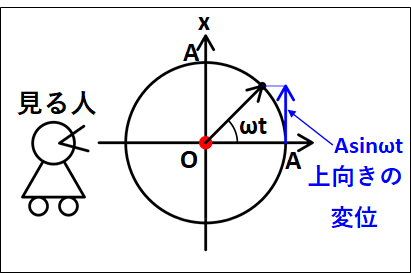
上向きの軸を\(x\)としたので、これは\(x\)軸への投射となります。
真横からみている人には、図中の左右方向の情報はわからないので、上下方向の情報のみがわかることになります。
よって、上下方向の変位のみを考えると、現在角度\(\omega{t}\)、半径\(A\)なので三角関数から上向きのベクトルは
\(+A\sin\omega{t}\)
となります。
これが、正射影されたグラフの\(x\)座標となるので、\(x=A\sin\omega{t}\)となります。
ここで、周期について考えてみます。
"1周まわる時間=周期\(T[s]\)"
なので、\(\displaystyle{\frac{1}{4}}\)回転なら\(\displaystyle{\frac{T}{4}[s]}\)となります。
よって、正射影のグラフで区間ごとに区切って載せていたのは、\(\displaystyle{\frac{1}{4}}\)回転ごとの区間となります。
また、先ほどみたように真横から見た振動の式は
\(x=A\sin\omega{t} \cdots①\)
先ほど説明したように、\(A\)を"振幅"といいます。
\(①\)式を変形すると
\(\displaystyle{\begin{eqnarray}x&=&A\sin\omega{t}\\\\&=&\sin\frac{2\pi}{\textcolor{blue}{\frac{2\pi}{\omega}}}t\end{eqnarray}}\)
となり、\(2\pi{t}\)の分母が周期となるので、
\(\displaystyle{x=\sin2\pi\frac{t}{\textcolor{blue}{T}}}\)
となり、周期は
\(\displaystyle{T=\frac{2\pi}{\omega}}\)
となることがわかります。
周期については、こちらも参考にしてください
→三角関数の定義と関係式
→三角関数のグラフ
\(\underline{\bf{②単振動と運動 方程式}}\)
単振動とは、運動方程式が
\(ma=-k(x-x_0)\)
の形になるものをいいます。
上式の形において、
"Kは正の値で"
"\(x_0\)は振動中心"
"\(-k(x-x_0)\)の部分を復元力"
と呼びます。

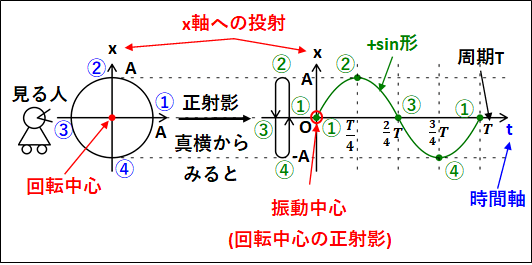
また、等速円運動の正射影や周期に関する話でみたように、真横からみて\(x\)軸へ投射された単振動の式は
\(\textcolor{red}{x=A\sin\omega{t}}\)
と表せます。
これを、時間\(t\)で微分したものが、速度\(v\)となります。
微分については、円運動で扱ったものとおなじようにします。
→円運動と慣性力
→微分法とその応用
実際に微分すると
\(\displaystyle{\textcolor{red}{v=\frac{dx}{dt}=A\omega\cos\omega{t}}}\)
さらに時間\(t\)で微分すると加速度となります。
\(\displaystyle{\textcolor{blue}{a=\frac{dv}{dt}=-A{\omega}^2\sin\omega{t}}}\)
ここで、\(\textcolor{green}{x=A\sin\omega{t}}\)なので、
\(\displaystyle{\begin{eqnarray}a&=&-{\omega}^2\textcolor{green}{A\sin\omega{t}}\\\\{\Leftrightarrow}a&=&-{\omega}^2\textcolor{green}{x}\end{eqnarray}}\)
となります。

上記では微分を用いて、変位の式から速度と加速度の式を導きましたが、速度、加速度を真横から見る人から考えることもできます。
等速円運動の部分で扱ったように、速度は大きさ\(r\omega\)で接線方向になります。
真横から見るひとには、この速度の上下方向の情報しかわからないので、下図のようになります。
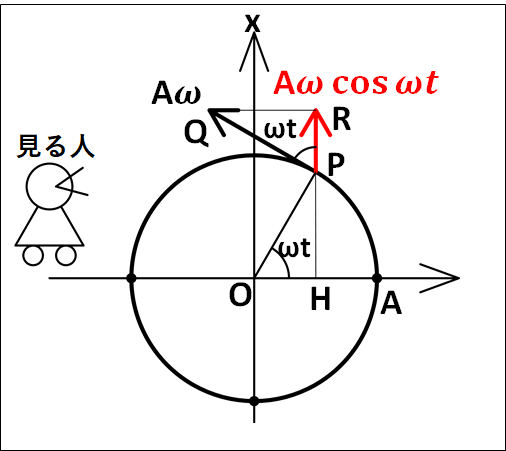
図中の赤いベクトルである\(\textcolor{red}{A\omega\cos\omega{t}}\)が、真横の人がみる速度ベクトル、すなわち単振動における速度となります。
※
図中に記した点\(O,H,P,Q,R\)について
\(Q\)
→円運動における速度ベクトルの終点
\(P\)
→円運動する物体の時刻\(t\)における位置
\(R\)
→円運動における速度ベクトルの上下方向成分の終点
\(\angle{PHO}=90°\)なので、\(\angle{OPH}=90°-\omega{t}\)
また、\(PQ\)は点Pにおける円の接線なので
\(\angle{OPQ}=90°\)
また、
\(\angle{OPH}+\angle{OPQ}+\angle{QPR}=180°\)
以上から、
\(\displaystyle{\begin{eqnarray}&&\angle{OPH}+\angle{OPQ}+\angle{QPR}=180°\\\\{\Leftrightarrow}&&(90°-\omega{t})+90°+\angle{QPR}=180°\\\\{\Leftrightarrow}&&\angle{QPR}=\omega{t}\end{eqnarray}}\)
となります。
これと、三角関数から円運動における速度の上下方向成分は
\(\displaystyle{\begin{eqnarray}\overrightarrow{PR}&=&|\overrightarrow{PQ}|\cos\omega{t}\\\\&=&A\omega\cos\omega{t}\end{eqnarray}}\)
となります。
加速度については、下図のように考えます。
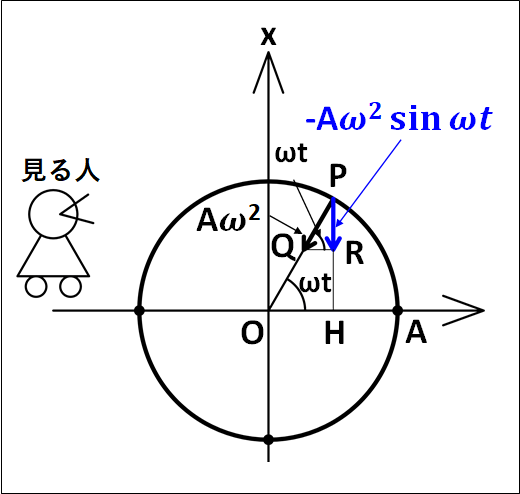
図中の青いベクトルである\(\textcolor{blue}{-A{\omega}^2\sin\omega{t}}\)が、真横の人がみる加速度ベクトル、すなわち単振動における加速度となります。
※
図中に記した点\(O,H,P,Q,R\)について
\(Q\)
→円運動における加速度ベクトルの終点
\(P\)
→円運動する物体の時刻(t)における位置
\(R\)
→円運動における加速度ベクトルの上下方向成分の終点
\(\overrightarrow{PQ}\)を上下左右方向に分解した上下方向のベクトルが\(\overrightarrow{PR}\)となります。
\(PR\)と\(Q R\)は直角なので、
\(Q R//OH\)
となります。
また、斜辺である\(OP\)は共通なので
\(\angle{POH}=\angle{PQR}=\omega{t}\)
これと、三角関数から円運動における加速度の上下方向成分は
\(\displaystyle{\begin{eqnarray}\overrightarrow{PR}=-|\overrightarrow{PQ}|\sin\omega{t}\\\\=-A{\omega}^2\sin\omega{t}\end{eqnarray}}\)
となります。
(いま上向き正で、速度の上下方向の成分は下向きなのでマイナスがつく)
以上のことから分かることは、
①運動方程式を変形して、
\(a=-□(x-x_0)\)
の\(□\)は\({\omega}^2\)を表す。
②
\(\displaystyle{a=-{\omega}^2x {\Leftrightarrow} ma=\textcolor{blue}{-m{\omega}^2x}}\)
上式の\(\textcolor{blue}{-m{\omega}^2x}\)部分を\(\textcolor{blue}{\bf{復元力}}\)と呼ぶ
2.単振動の運動方程式の解き方
\(\displaystyle{\begin{eqnarray}ma=-k(x-x_0)\\\\{\Leftrightarrow}a=-\textcolor{red}{\frac{k}{m}}(x-x_0)\end{eqnarray}}\)
上式の変位\(x\)の係数である\(\displaystyle{\textcolor{red}{\frac{k}{m}}}\)が、角振動数\(\omega\)の情報を与えます。
(\(a=-{\omega}^2x\)から)
これより、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
となります。
(高校物理においては、角振動数は正として扱ってよい)
このとき、
\(\displaystyle{a=-\frac{k}{m}(\textcolor{green}{x-x_0})}\)
の\( (\textcolor{green}{x-x_0})\)をそのまま左辺にもってきて
\(\displaystyle{\textcolor{green}{x-x_0}=±A\cos\left(\sqrt{\frac{k}{m}}t\right)}\)
または
\(\displaystyle{\textcolor{green}{x-x_0}=±B\sin\left(\sqrt{\frac{k}{m}}t\right)}\)
となります。
上式の\(±\sin\)や\(±\cos\)のうちのどの形をとるかは、問題で判断します。

3.単振動の一般解
単振動の一般解には、三角関数の合成式
\(\displaystyle{A\cos\theta+B\sin\theta=\sqrt{A^2+B^2}\sin(\theta+\alpha)}\)
を用います。
合成式についてはこちら
→三角関数の公式
\(\theta\)を\(\omega{t}\)とすると、
\(\displaystyle{A\cos\omega{t}+B\sin\omega{t}=\sqrt{A^2+B^2}\sin(\omega{t}+\alpha)}\)
となります。
ここで、
\(\displaystyle{\sqrt{A^2+B^2}}\)で振幅が
\(\displaystyle{\omega}\)は\(\displaystyle{\omega=\frac{2\pi}{T}}\)によって周期が
\(\alpha\)によって、\(t\)軸方向にどれだけ平行移動しているか
がそれぞれ決まるので、
\(\displaystyle{\sqrt{A^2+B^2}\sin(\omega{t}+\alpha)}\)
はどのような波の式(単振動の式)も表すことができます。
すなわち、
\(\displaystyle{A\cos\omega{t}+B\sin\omega{t}}\)
もどのような波(単振動)の式も表すことができます。
これによって、
\(\displaystyle{x-x_0=A\cos\omega{t}+B\sin\omega{t}}\)
において、定数\(A , B\)が決まれば、単振動による物体の位置が表せることになります。
また、位置の式
\(\displaystyle{x-x_0=A\cos\omega{t}+B\sin\omega{t}}\)
を時間\(t\)で微分すると速度\(v\)が、速度\(v\)の式を時間\(t\)で微分すると加速度\(a\)が求まります。
これらを用いて、初期条件(\(t=0\)のときの条件)から定数\(A , B\)を定めることで、物体の位置・速度・加速度の情報を得ることができます。
したがって、単振動する物体の位置を表す式の一般解は次のようになります。
\(\textcolor{green}{\underline{\bf{単振動する物体の位置を表す一般解}}}\)
\(\displaystyle{\textcolor{green}{x-x_0=A\cos\omega{t}+B\sin\omega{t}}}\)
4.運動方程式解き方練習
例)
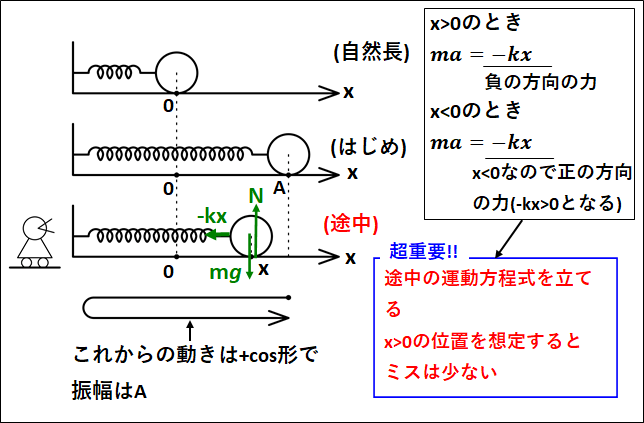
図のようにばねにつながれた質量\(m\)の物体を、自然長から\(A\)だけ伸ばした状態で静かに放すことを考える。
(ばね定数は\(k\)、床はなめらかとする)
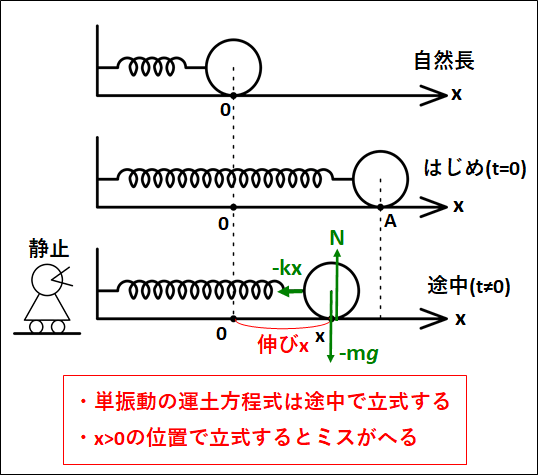
途中での\(x\)方向に関する運動方程式は、
(途中での物体の位置を\(x\)とする)
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\\\\{\Leftrightarrow}&&a=-\frac{k}{m}(x-0)\end{eqnarray}}\)
※よくあるミス
\(× ma=-kA\)
\(× ma=kx\)
よって、
\(\displaystyle{{\omega}^2=\frac{k}{m}}\)
から、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
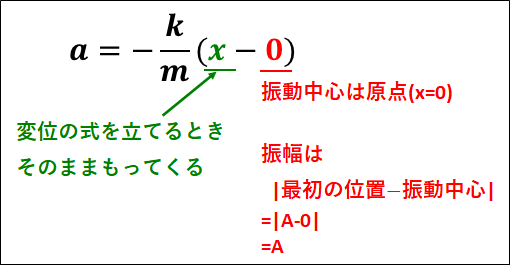
振動中心は\(x=0\)
※
\(\displaystyle{\textcolor{red}{a=-\frac{k}{m}(x-x_0)}}\)
において、振動中心は\(x_0\)
今回は、\(x_0=0\)なので、振動中心は\(x=0\)の位置となる
物体は、はじめ\(A\)の位置にいて、そこから負の方向へ動き出し、\(x=0\)を振動中心として振動する。
よって、下図のように\(①→②→③→④→①\)のように動きます。
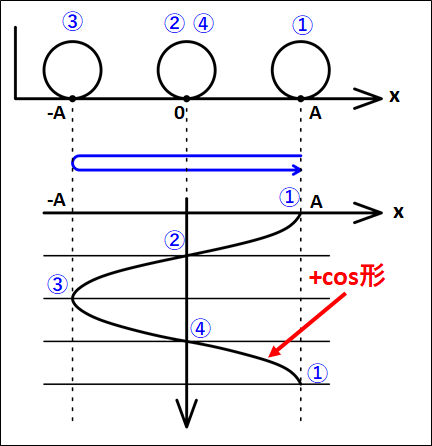
グラフの形は、はじめ正の位置にいて、そこから\(0\)→負→\(0\)→正のように動いていきます。
なので、これは\(\textcolor{red}{+\cos}\)形となります。
また振幅は、振動中心からの最も離れるときの距離なので
\(\textcolor{red}{\bf{振幅=|最初の位置-振動中心|}}\)
となり、今回は
\(\displaystyle{\begin{eqnarray}{\bf{振幅}}&=&{\bf{|最初の位置-振動中心|}}\\\\&=&|A-0|\\\\&=&A\end{eqnarray}}\)
となります。
以上から、物体の変位の式は運動方程式の解き方で解説したように、\(x-0\)をそのままもってきて
\(\displaystyle{\begin{eqnarray}x-0&=&A\cos\omega{t}\\\\&=&A\cos\sqrt{\frac{k}{m}}t\\\\&=&A\cos2\pi\frac{t}{\textcolor{green}{2\pi\sqrt{\frac{m}{k}}}}\end{eqnarray}}\)
上式における\(2\pi{t}\)の分母が周期となるので、周期\(T\)は
\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}}\)
変位の式は
\(\displaystyle{x=A\cos\sqrt{\frac{k}{m}}t}\)
速度の式を求めるために、変位の式を時間\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
これは、\(-\sin\)形となります。
さらに、加速度の式を求めるために、速度の式を時間\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A\frac{k}{m}\cos\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
これは、\(-\cos\)形となります。
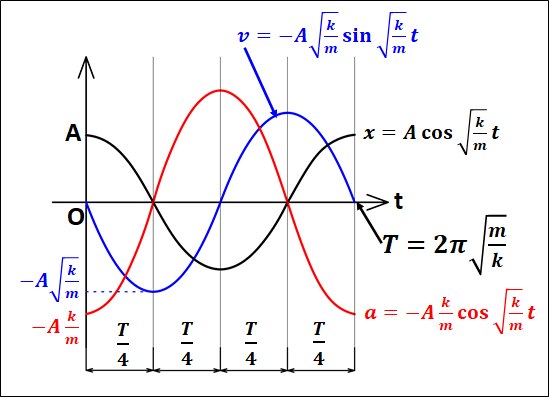
次に求めた変位・速度・加速度の関係をグラフで表すと、下図のようになります。
(変位・速度・加速度それぞれの最大値の大小関係は適当)
\(\underline{\bf{※一般解を用いると}}\)
運動方程式を立てて、振動中心\(x=0\)および、角振動数\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)までは求めているとします。
単振動の変位の式の一般解から、
(例題で最初の伸びに\(A\)が使われているので、一般解において\(A\)を\(A'\)とした)
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t} \cdots①}\)
\(t\)で微分して
\(\displaystyle{v=-A'\omega\sin\omega{t}+B'\omega\cos\omega{t} \cdots②}\)
さらに\(t\)で微分して
\(\displaystyle{a=-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t} \cdots③}\)
初期条件(\(t=0\)のときの条件)は、
\(t=0\)のとき、\(x=A\)、\(v=0\)
なので、これらを\(①、②\)に代入すると、
\(①\)から
\(\displaystyle{\begin{eqnarray}&&A=A'\cos0+B'\sin0\\\\{\Leftrightarrow}&&A=A'\end{eqnarray}}\)
(\(\cos0=1 , \sin0=0\))
\(②\)から
\(\displaystyle{\begin{eqnarray}&&0=-A'\omega\sin0+B'\omega\cos0\\\\{\Leftrightarrow}&&B'=0\end{eqnarray}}\)
以上から、\(A'=A , B'=0\)を\(①,②,③\)にそれぞれ代入すると
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
\(\displaystyle{ \begin{eqnarray} v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\sqrt{\frac{k}{m}}t \end{eqnarray} }\)
\(\displaystyle{ \begin{eqnarray} a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\sqrt{\frac{k}{m}}t \end{eqnarray} }\)
と、先ほどみた式と同じ式がでてきます。
5.水平ばね振り子
先ほどみた例と同じとなりますが…
なめらかな水平面上に、一端を固定したばね(ばね定数\(k\))の多端に質量\(m\)のおもりをつなぎます。
下図のような状態で、ばねを\(A\)だけ引き伸ばし、静かに手を離したときのおもりの運動をみてみます。
(自然長の位置を原点とする)
上記の、"ばねを\(A\)だけ引き伸ばし、静かに手を離す"という部分が初期条件(\(t=0\)のときの条件)となります。
\(x\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\\\\{\Leftrightarrow}&&a=-\frac{k}{m}(\textcolor{green}{x}-\textcolor{red}{0})\end{eqnarray}}\)
よって、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
また、\((\textcolor{green}{x}-\textcolor{red}{0})\)から、
振動中心は原点で、振幅は
\(|A-0|=A\)
であることがわかります。
以上から、グラフが\(+\cos\)形であることに注意して、変形した運動方程式の\(\textcolor{green}{x}\)をそのまま左辺にもってきて、変位の式を立てると
\(\displaystyle{\begin{eqnarray}\textcolor{green}{x}&=&\textcolor{red}{A\cos}\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
上式の、
\(\displaystyle{\textcolor{red}{+A\cos}}\)
は問題から読み取る情報となります。
また、\(2\pi{t}\)の分母が周期\(T\)となることから
\(\displaystyle{\textcolor{blue}{T=2\pi\sqrt{\frac{m}{k}}}}\)
となります。
上記変位の式を\(t\)で微分して、
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(2\pi\frac{t}{2\pi\sqrt{\frac{m}{k}}}\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\frac{k}{m}\cos\left(2\pi\frac{t}{2\pi\sqrt{\frac{m}{k}}}\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。
(例で扱ったものとおなじ)

一般解を用いても同様にして
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t}}\)
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}\end{eqnarray}}\)
初期条件\(t=0\)のとき、\(x=A , v=0\)を上式に代入して
\(A'=A , B'=0\)
と決まります。
6.鉛直ばね振り子
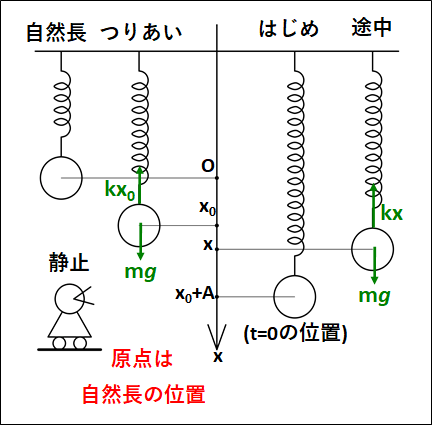
ばね定数\(k\)のばねを天井からつるし、他端に質量\(m\)のおもりを静かにつるすと、伸びが\(x_0\)になって静止したとする。
静止した位置からおもりをさらに\(A\)だけ引いて静かに離すことを考える。
(軸は鉛直下向き)
状況を図示すると、下図のようになります。
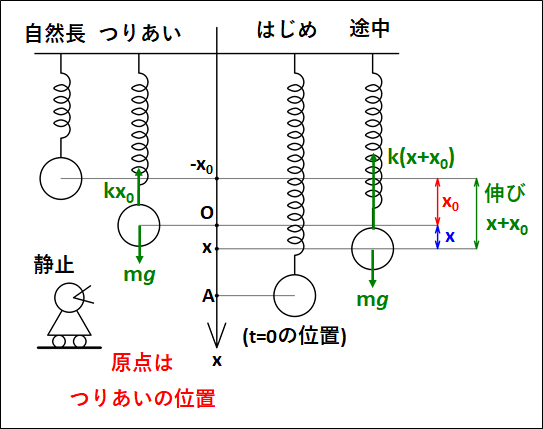
"\(\textcolor{red}{\bf{つりあいの位置}}\)を原点"としています。
まず、つりあっているときに関してですが、上下方向のつりあいより
\(kx_0=mg\)
次に途中の物体の位置を\(x\)とすると運動方程式は、
\(\displaystyle{\begin{eqnarray}&&ma=mg-k(x+x_0)\\\\{\Leftrightarrow}&&ma=mg-kx-kx_0\end{eqnarray}}\)
途中での自然長からの伸びは\(x\)ではなく、\(x+x_0\)であることに注意してください。
また、つりあいの式 \(kx_0=mg\) から、
\(\displaystyle{\begin{eqnarray}&&ma=mg-kx-kx_0\\\\{\Leftrightarrow}&&ma=\textcolor{red}{\cancel{\textcolor{black}{mg}}}-kx-\textcolor{red}{\cancel{\textcolor{black}{mg}}}\\\\{\Leftrightarrow}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\end{eqnarray}}\)
より、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
となります。
また、つりあいの位置を原点にしたことで、運動方程式がきれいな形になっていることを確認してください。
振動の形は、\(t=0\)で\(x=A\gt0\)。
そこから、\(x\)の負の方向へと運動するので\(+\cos\)形となります。
(\(+\cos\)のグラフも正→0→負→0→正と変化していく)
また、振動中心は\(x=0\)、振幅は
\(|A-0|=A\)
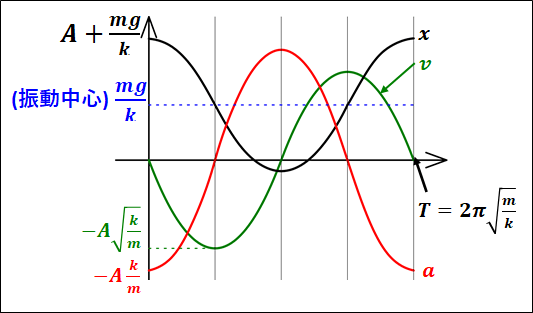
よって、変位の式は
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
周期\(T\)は、\(2\pi{t}\)の分母なので
\(\displaystyle{\textcolor{blue}{T=2\pi\sqrt{\frac{m}{k}}}}\)
変位の式を、\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\frac{k}{m}\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。

一般解を用いると、
初期条件\(t=0\)で\(x=A , v=0\)から定数\(A , B\)が決まります。
初期条件と角振動数が同じなので、水平ばね振り子と同じ式になります。
\(\underline{\bf{<類題>}}\)
先ほどの鉛直ばね振り子において、自然長を原点とするとどうなるのか?
状況は下図のようになります。
つりあい位置での上下方向のつりあいより
\(kx_0=mg\)
はじめの位置は、つりあいの位置からさらに\(A\)だけ下げたところになるので、座標は\(x_0+A\)になることに注意してください。
また、今回は自然長の位置を原点にしているので、途中の位置\(x\)におけるばねの自然長からの伸びは\(x\)となり、弾性力は上向きに\(kx\)となります。
よって、途中の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&ma=mg-kx\\\\{\Leftrightarrow}&&ma=-k\left(x-\frac{mg}{k}\right)\\\\{\Leftrightarrow}&&a=-\frac{k}{m}\left(x-\textcolor{red}{\frac{mg}{k}}\right)\end{eqnarray}}\)
これより、角振動数は
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
振動中心は
\(\displaystyle{x=\frac{mg}{k}=x_0}\)
となります。
(つりあいの式\(kx_0=mg\)を式変形すると、\(\frac{mg}{k}=x_0\)となる)
振幅は、|はじめの位置-振動中心| から、
\(\displaystyle{\begin{eqnarray}|x_0+A-\frac{mg}{k}|&=&|x_0+A-x_0| (∵\frac{mg}{k}=x_0)\\\\&=&A\end{eqnarray}}\)
よって、この物体の運動は\(x=x_0=\frac{mg}{k}\)を振動中心として振幅\(A\)で振動することが分かります。
また、振動の形はつりあいの位置を原点にとったときと同様に\(+\cos\)形です。
よって、変位の式は
\(\displaystyle{x-\frac{mg}{k}}\)
をそのまま左辺にもってきて
\(\displaystyle{\begin{eqnarray}&&x-\frac{mg}{k}=A\cos\omega{t}\\\\{\Leftrightarrow}&&x-\frac{mg}{k}=A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\{\Leftrightarrow}&&x=A\cos\left(\sqrt{\frac{k}{m}}t\right)+\frac{mg}{k}\\\\{\Leftrightarrow}&&x=A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)+\frac{mg}{k}\end{eqnarray}}\)
上式は、\(x=A\cos\left(\sqrt{\frac{k}{m}}t\right)\)のグラフを、\(x\)軸方向に\(+\frac{mg}{k}\)平行移動したものとなります。
三角関数のグラフの平行移動についてはこちら
→三角関数のグラフ
またこれまでと同様に、\(2\pi{t}\)の分母が周期なので、
\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}}\)
求めた変位の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。
一般解を用いると、
\(\displaystyle{a=-\frac{k}{m}(x-\frac{mg}{k})}\)
から、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
また、振動中心
\(\displaystyle{x=\frac{mg}{k}}\)
よって、
\(\displaystyle{x-\frac{mg}{k}=A'\cos\omega{t}+B'\sin\omega{t}}\)
変位の一般解の式を\(t\)で微分して
\(\displaystyle{v=-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}}\)
速度の式を\(t\)で微分して
\(\displaystyle{a=-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}}\)
初期条件\(t=0\)で\(x=x_0+A\)、\(v=0\)なので、まず変位の式に代入して
\(\displaystyle{\begin{eqnarray}x_0+A-\frac{mg}{k}=A'\cos0+B'\sin0\end{eqnarray}}\)
\(\displaystyle{x_0=\frac{mg}{k}}\)なので、
\(\displaystyle{\begin{eqnarray}&&x_0+A-\frac{mg}{k}=A'\cos0+B'\sin0\\\\{\Leftrightarrow}&&\frac{mg}{k}+A-\frac{mg}{k}=A'×1+B'×0\\\\{\Leftrightarrow}&&A'=A\end{eqnarray}}\)
次に、速度の式に代入して
\(\displaystyle{\begin{eqnarray}&&0=-A'\omega\sin0+B'\omega\cos0\\\\{\Leftrightarrow}&&B'=0\end{eqnarray}}\)
\(A'=A , B'=0\)をそれぞれの式に戻すと、
\(\displaystyle{\begin{eqnarray}&&x-\frac{mg}{k}=A\cos\omega{t}\\\\{\Leftrightarrow}&&x=A\cos\left(\sqrt{\frac{k}{m}}t\right)+\frac{mg}{k}\end{eqnarray}}\)
\(\displaystyle{v=-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}\right)}\)
\(\displaystyle{a=-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}\right)}\)
と、先ほどみた式と同じものになります。
7.単振り子
糸の上端を固定して、下端におもりをつけ、おもりを\(\textcolor{red}{\bf{わずか}}\)に引いて静かに手を離す。
(糸の長さを\(l\)、おもりを\(A\)だけ引くとする)
下図のようにはじめと途中、また糸が鉛直になるときを考えます。
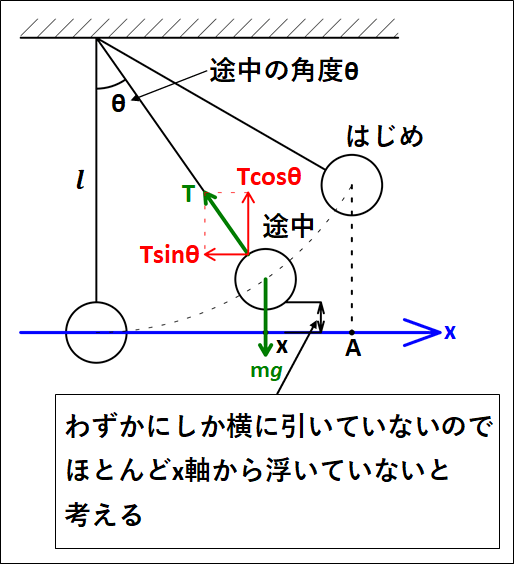
途中の\(x\)座標を\(x\)、そのときの鉛直な方向と糸のなす角を\(\theta\)とします。
また、図ではおおげさに描いていますが、実際はわずかにしか引いていないので、おもりはほとんど\(x\)軸上を運動することになります。
以上から、おもりは\(x\)軸上を運動し、鉛直方向には静止する(つりあう)と考えて運動方程式とつりあいの式を立てると
\(\displaystyle{\begin{eqnarray}&&{\bf{おもりをわずかに振る}}\\\\{\Leftrightarrow}&&{\bf{おもりはx軸からほとんど離れない}}\\\\{\Leftrightarrow}&&{\bf{おもりはx軸上で横方向に振動する}}\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}T\cos\theta=mg {\bf{(上下のつりあい)}}\\\\ma=-T\sin\theta {\bf{水平方向の運動 方程式}}\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}T=\frac{mg}{\cos\theta}\\ma=-\frac{mg}{\cos\theta}×\sin\theta=-mg\tan\theta\end{array}\right.\end{eqnarray}}\)
よって、
\(\displaystyle{ma=-mg\tan\theta}\)
※ちなみに、\(\theta\)が非常に小さいとき、
\(\tan\theta≒\sin\theta≒\theta\)
と近似ができる。
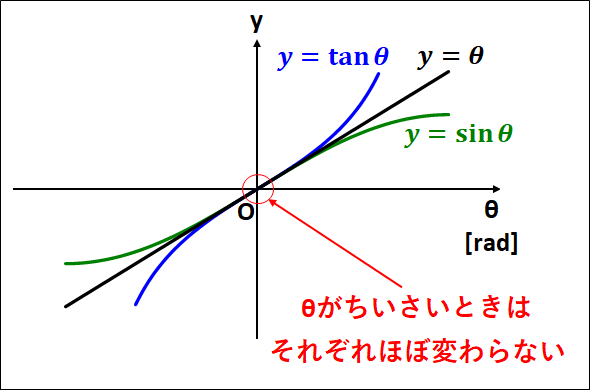
この近似を用いると以下のようになる。
\(\displaystyle{\begin{eqnarray}&& ma=-mg\tan\theta\\\\&&\left(\begin{array}{l}{\Leftrightarrow}ma≒-mg\tan\theta\\\\{\Leftrightarrow}a≒-g\tan\theta\end{array}\right)\end{eqnarray}}\)
\(\tan\theta\)は下図のようになります。
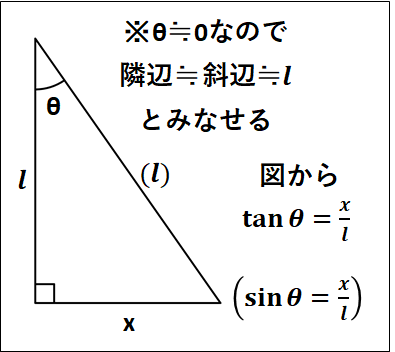
これを用いて、さらに運動方程式を変形していくと、
\(\displaystyle{\begin{eqnarray}&&ma=-mg\tan\theta\\\\{\Leftrightarrow}&&ma≒-mg\frac{x}{l}\\\\{\Leftrightarrow}&&a≒-\frac{g}{l}x\end{eqnarray}}\)
以上から、
角振動数:
\(\displaystyle{\omega=\frac{g}{l}}\)
振動中心:
\(x=0\)
振幅:
\(|A-0|=A\)
であることが分かります。
また、単振動の形は(正→0→負→0→正)のように変化していくので、\(+\cos\)形になります。
よって、変位の式は
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{g}{l}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{l}{g}}}}\right)\end{eqnarray}}\)
これより、周期は\(T\)は\(2\pi{t}\)の分母なので、
\(\displaystyle{T=2\pi\sqrt{\frac{l}{g}}}\)
となります。
また、変位の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{g}{l}}\sin\left(\sqrt{\frac{g}{l}}t\right)\end{eqnarray}}\)
さらに速度の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{g}{l}\cos\left(\sqrt{\frac{g}{l}}t\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは以下のようになります。
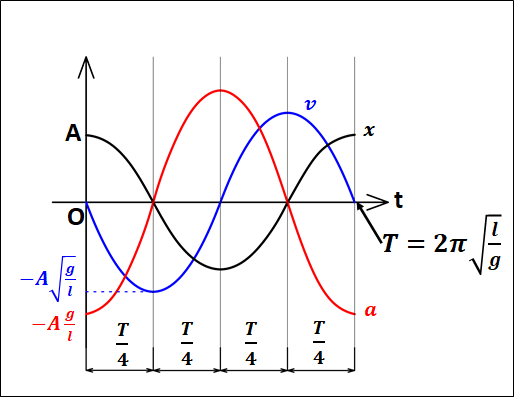
上記から、振り子の周期において\(2\pi\)と\(g\)は定数となります。
よって、単振り子の周期は振幅が小さければ振り子の長さ\(l\)だけで決まることになります。
このように、周期が振幅によらずに振り子の長さだけで決まることを、\(\textcolor{red}{\bf{振り子の等時性}}\)といいます。
一般解を用いると、
運動方程式から、
角振動数
\(\displaystyle{\omega=\sqrt{\frac{g}{l}}}\)
振動中心
\(x=0\)
振幅
\(A\)
がわかります。
よって、一般解から
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t}}\)
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}\end{eqnarray}}\)
初期条件\(t=0\)のとき、\(x=A , v=0\)を上式に代入して
\(A'=A , B'=0\)
と決まります。
これを元に戻すと先ほどの同様の式
\(\displaystyle{x=A\cos\omega{t}}\)
\(\displaystyle{v=-A\omega\sin\omega{t}}\)
\(\displaystyle{a=-A{\omega}^2\cos\omega{t}}\)
が得られます。
8.単振動のエネルギー
振動する物体の時間による位置が
\(\displaystyle{x=A\cos\omega{t}}\)
で表されているとします。
※
運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\end{eqnarray}}\)
より
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
このとき、
\(\displaystyle{x=A\cos\omega{t}}\)
上式を\(t\)で微分して
\(\displaystyle{v=-A\omega\sin\omega{t}}\)
速度の式を\(t\)で微分して
\(\displaystyle{a=-A{\omega}^2\cos\omega{t}}\)
ここで、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&{\bf{単振動のエネルギー}}\\\\=&&{\bf{物体の運動エネルギー+ばねの弾性力による位置 エネルギー}}\end{eqnarray}}}\)
となります。
ここから、
\(\underline{\bf{教科書的に…}}\)
単振動のエネルギー(エネルギーの和)は、物体の運動エネルギーとばねの弾性力による位置エネルギーの和なので、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&{\bf{単 振動のエネルギー}}\\\\=&&{\bf{物体の運動エネルギー+ばねの弾性力による位置 エネルギー}}\\\\&&=\frac{1}{2}m\textcolor{red}{v}^2+\frac{1}{2}k\textcolor{red}{x}^2\end{eqnarray}}}\)
上式の形から、\(\textcolor{red}{v}\)と\(\textcolor{red}{x}\)に単振動の式を代入できます。
実際に代入すると
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}m\textcolor{red}{v}^2+\frac{1}{2}k\textcolor{red}{x}^2\\\\=&&\frac{1}{2}m(\textcolor{red}{-A\omega\sin\omega{t}})^2+\frac{1}{2}k(\textcolor{red}{A\cos\omega{t}})^2\\\\=&&\frac{1}{2}mA^2{\omega}^2\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t}\\\\=&&\frac{1}{2}mA^2\frac{k}{m}\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t} \left(∵\omega=\sqrt{\frac{k}{m}}\right)\\\\=&&\frac{1}{2}kA^2\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t}\\\\=&&\frac{1}{2}kA^2(\sin^2\omega{t}+\cos^2\omega{t})\\\\=&&\frac{1}{2}kA^2 (一定)\end{eqnarray}}}\)
また、
\(\displaystyle{{\omega}^2=\frac{k}{m}{\Leftrightarrow}k=m{\omega}^2}\)
から、
\(\displaystyle{\frac{1}{2}kA^2=\frac{1}{2}(m{\omega}^2)A^2 (一定)}\)
また、
\(\displaystyle{\omega=\frac{2\pi}{T}=2\pi{f}}\)
を用いると、
\(\displaystyle{\begin{eqnarray}&&\frac{1}{2}\left\{m(2\pi{f})^2\right\}A^2\\\\=&&2m{\pi}^2f^2A^2 (一定)\end{eqnarray}}\)
以上から、単振動のエネルギーは時間に関係なく、一定になります。
\(\underline{\bf{大学的に…}}\)
\(\textcolor{green}{\bf{エネルギー積 分}}\)
運動方程式の両辺に\(v\)を掛けて
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&m\textcolor{red}{v}a=-kx\textcolor{red}{v}\end{eqnarray}}\)
ここで、速度と加速度の定義
\(\displaystyle{\textcolor{red}{v=\frac{dx}{dt} , a=\frac{dv}{dt}}}\)
から、運動方程式の変形を続けて
\(\displaystyle{\begin{eqnarray}&&m\textcolor{red}{v}a=-kx\textcolor{red}{v}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=-kx\frac{dx}{dt}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}+kx\frac{dx}{dt}=0\end{eqnarray}}\)
ここで、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\frac{1}{2}mv^2&=&\frac{dv}{dt}\frac{d}{dv}\frac{1}{2}mv^2\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\frac{1}{2}kx^2&=&\frac{dx}{dt}\frac{d}{dx}\frac{1}{2}kx^2\\\\&=&kx\frac{dx}{dt}\end{eqnarray}}\)
から、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}+kx\frac{dx}{dt}=0\\\\=&&\frac{d}{dt}\left(\frac{1}{2}mv^2+\frac{1}{2}kx^2\right)=0\end{eqnarray}}\)
以上から、
\(\displaystyle{\frac{1}{2}mv^2+\frac{1}{2}kx^2}\)
は時間\(t\)で微分すると\(0\)になるので、定数となります。
すなわち、上式は時間によらずに一定になります。
※
エネルギー積分については、こちらの力学的エネルギー保存の法則も参考にしてください。
→仕事とエネルギー
12.円運動と慣性力
この記事では等速円運動と慣性力について扱っています。
特に、円運動の速度と加速度については微分を用いた解説と、微分を用いていない解説を載せています。
個人的には、微分を用いた方がすっきりしているのでおすすめですが、公式的なものを覚えるのが苦痛でないならどちらの解説を参考にしてもらってもよいです。
慣性力については、これを用いる際の長所と短所などのついて載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.角速度と周期
円周上を一定の速さで動く運動を\(\textcolor{red}{\bf{等速円運動}}\)といいます。
円運動においては、直線の運動と区別するために、時間\(t[s]\)のかわりに\(\textcolor{red}{{\bf{周期}}T[s]}\)を、速度\(v[m/s]\)のかわりに\(\textcolor{red}{{\bf{角速度}}\omega[rad/s]}\)(\(\omega\)はオメガと読む)を用います。
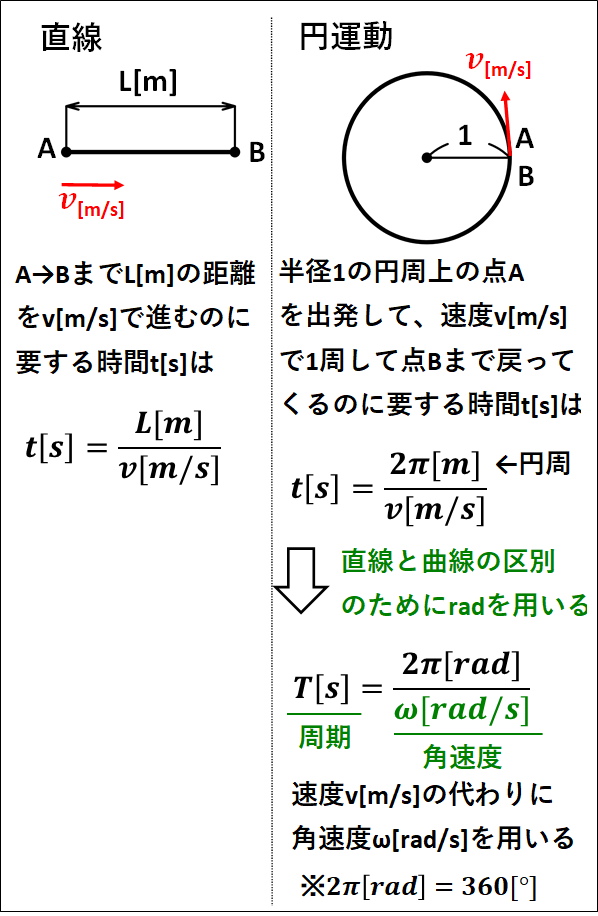
角速度\(\omega[rad/s]\)と周期\(T[s]\)については、また詳しく説明しますが、とりあえず直線と円運動の比較を載せておきます。
角度\(rad\)や、単位円の扱いについてはこちらも参考にしてください
→三角関数の定義と関係式
\(\underline{{\bf{○角速度}}\omega[rad/s]}\)
単位時間(1秒)あたりにどれだけの角度(\(rad\))進むかを表す量。
\(\omega[rad/s]\)は1秒間にどれだけの角度を進むかを表すので、\(t[s]\)間の間に進んだ角度は
\(\omega[rad/s]×t[s]=\omega{t}[rad]\)
となります。
これは数学の三角関数で扱う\(\theta[rad]\)の単位と同じであり、\(\omega{t}\)は角度を表すことが分かると思います。
\(\underline{{\bf{○周期}}T[s]}\)
円を1回転するのに何秒かかるかを表す量。
単位は\(s\)(秒)ですが、分かりやすくするために便宜的に\(s/(回)\)と考えると良いと思います。
また、1秒間に何回転するかを表す回転数\(n[/s]\)は、\(n[(回)/s]\)と考えると周期の逆数と単位が同じであることが分かると思います。
よって、
\(\displaystyle{\begin{eqnarray}n[/s]=\frac{1}{T[s]}\end{eqnarray}}\)
\(\displaystyle{\left(n[(回)/s]=\frac{1}{T[s/(回)]}\right)}\)
上記のように、1回転するのに何秒かかるかの逆数をとると、1秒間に何回転するかになります。
また、単位\([/s]\)は\([Hz]\)(ヘルツ)とも書きます。
2.等速円運動とベクトル図(微分有り)
半径\(r\)の円周上の点\(A\)を出発して\(t[s]\)後の点\(P\)を考えます。
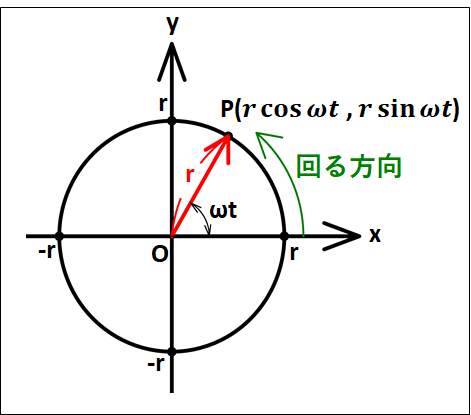
ここで、\(\overrightarrow{OP}\)を成分表示すると、次のようになります。
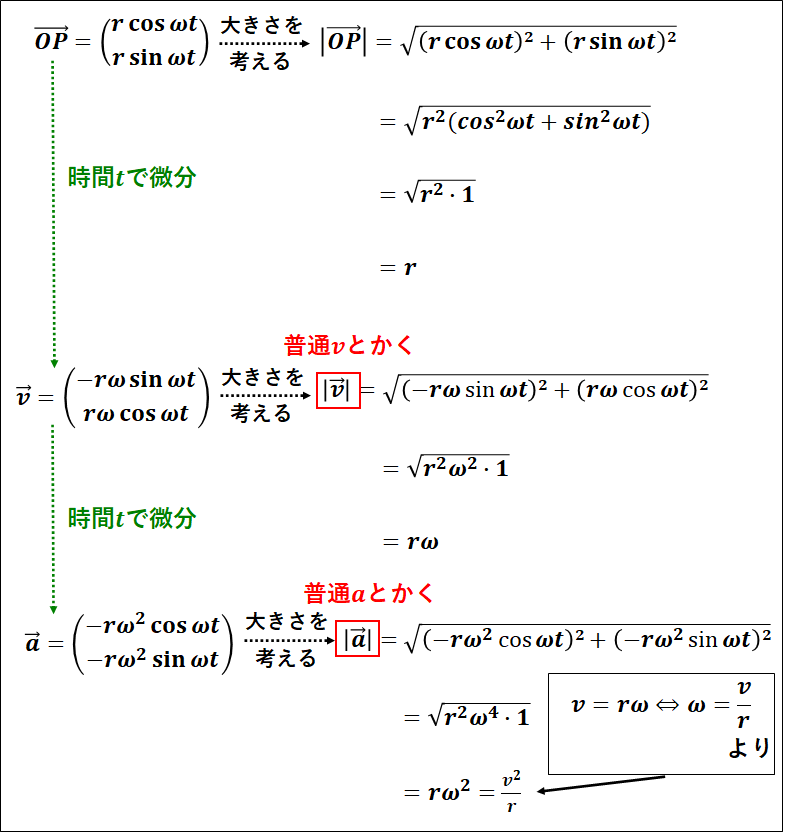
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}r\cos\omega{t}\\r\sin\omega{t}\end{array}\right)}\)
※円周上の点と、ベクトルの成分表示についてはこちら
→三角関数の定義と関係式
→力とベクトル
\(\overrightarrow{OP}\)の大きさを考えると、
\(\displaystyle{\begin{eqnarray}|\overrightarrow{OP}|&=&\sqrt{(r\cos\omega{t})^2+(r\sin\omega{t})^2}\\\\&=&\sqrt{r^2(\cos^2\omega{t}+\sin^2\omega{t})}\\\\&=&\sqrt{r^2}\\\\&=&r\end{eqnarray}}\)
となります。
これは図からも、\(\overrightarrow{OP}\)の長さと、単位円上の点\(P\)と原点\(O\)を結ぶ線分の長さがともに半径\(r\)であることから分かります。
次に速度と加速度、またその大きさを考えていきます。
速度は位置を時間\(t\)で微分したもの、加速度は速度を時間\(t\)で微分したものでした。
→変位・速度・加速度
実際に位置ベクトル\(\overrightarrow{OP}\)の成分を、それぞれ\(t\)で微分します。
等速円運動では、\(r\)と\(\omega\)が一定であることに注意してください。(定数として扱う)
\(\cos\omega{t}\)について、\(\omega{t}=u\)とおくと
\(\displaystyle{\begin{eqnarray}&&\frac{d}{dt}\cos\omega{t}\\\\=&&\frac{d}{du}\cos{u}\frac{du}{dt}\\\\=&&\frac{d}{du}\cos{u}\frac{d}{dt}\omega{t}\\\\=&&-\sin{u}・\omega\\\\=&&-\omega\sin\omega{t}\end{eqnarray}}\)
※合成関数の微分を用いた
→微分法とその応用

よって、\(x\)成分の速度は\(x=r\cos\omega{t}\)とおくと
\(\displaystyle{\begin{eqnarray}v_x&=&\frac{dx}{dt}\\\\&=&\frac{d}{dt}r\cos\omega{t}\\\\&=&r\frac{d}{dt}\cos\omega{t}\\\\&=&-r\omega\sin\omega{t}\end{eqnarray}}\)
となります。
同様にして、\(y\)成分\(y=r\sin\omega{t}\)も\(t\)で微分すると
\(\displaystyle{\begin{eqnarray}v_y&=&\frac{dy}{dt}\\\\&=&\frac{d}{dt}r\sin\omega{t}\\\\&=&r\omega\cos\omega{t}\end{eqnarray}}\)
以上から、
\(\displaystyle{\begin{eqnarray}\vec{v}&=&\left(\begin{array}{c}v_x\\v_y\end{array}\right)\\\\&=&\left(\begin{array}{c}-r\omega\sin\omega{t}\\r\omega\cos\omega{t}\end{array}\right)\end{eqnarray}}\)
大きさを考えると、
\(\displaystyle{\begin{eqnarray}|\vec{v}|&=&\sqrt{v_x^2+v_y^2}\\\\&=&\sqrt{(-r\omega\sin\omega{t})^2+(r\omega\cos\omega{t})^2}\\\\&=&\sqrt{r^2{\omega}^2}\\\\&=&r\omega\end{eqnarray}}\)
ふつうは、\(|\vec{v}|\)を単に\(v\)と書きます。
加速度も同様にして、速度の成分を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a_x&=&\frac{dv_x}{dt}\\\\&=&\frac{d}{dt}(-r\omega\sin\omega{t})\\\\&=&-r{\omega}^2\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a_y&=&\frac{dv_y}{dt}\\\\&=&\frac{d}{dt}(r\omega\cos\omega{t})\\\\&=&-r{\omega}^2\sin\omega{t}\end{eqnarray}}\)
以上から、
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\left(\begin{array}{c}a_x\\a_y\end{array}\right)\\\\&=&\left(\begin{array}{c}-r{\omega}^2\cos\omega{t}\\-r{\omega}^2\sin\omega{t}\end{array}\right)\end{eqnarray}}\)
大きさは、
\(\displaystyle{\begin{eqnarray}|\vec{a}|&=&\sqrt{a_x^2+a_y^2}\\\\&=&\sqrt{(-r{\omega}^2\cos\omega{t})^2+(-r{\omega}^2\sin\omega{t})^2}\\\\&=&\sqrt{r^2{\omega}^4}\\\\&=&r{\omega}^2\\\\&=&r\left(\frac{v}{r}\right)^2\\\\&=&\frac{v^2}{r}\end{eqnarray}}\)
ふつうは、\(|\vec{a}|\)を単に\(a\)と書きます。
上式の、\(r{\omega}^2\)について、速度の大きさの部分で見たように
\(\displaystyle{\begin{eqnarray}v=r\omega {\Leftrightarrow} \omega=\frac{v}{r}\end{eqnarray}}\)
なので、これを\(a=r{\omega}^2\)に代入して
\(\displaystyle{\begin{eqnarray}a&=&r{\omega}^2\\\\&=&\frac{v^2}{r}\end{eqnarray}}\)
となります。
以上のことをまとめておきます。
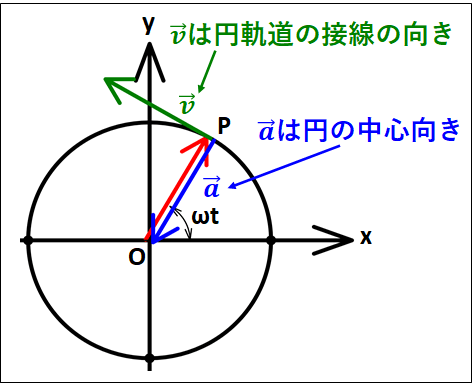
次に、この位置と速度と加速度のベクトルの向きをみていきます。
\(\underline{\bf{○位置ベクトル}}\)
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}r\cos\omega{t}\\r\sin\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\overrightarrow{OP}=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の正の方向に1進んで、\(y\)軸の正の方向に1進む向きです。
\(\underline{\bf{○速度ベクトル}}\)
\(\displaystyle{\vec{v}=\left(\begin{array}{c}-r\omega\sin\omega{t}\\r\omega\cos\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r\omega=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\vec{v}=\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の負の方向に1進んで、\(y\)軸の正の方向に1進む向きです。
\(\underline{\bf{○加速度ベクトル}}\)
\(\displaystyle{\vec{a}=\left(\begin{array}{c}-r{\omega}^2\cos\omega{t}\\-r{\omega}^2\sin\omega{t}\end{array}\right)}\)
上式において、
\(\displaystyle{r{\omega}^2=1 , \omega{t}=\frac{1}{2}\pi(=45°)}\)
のとき
\(\displaystyle{\vec{a}=\left(\begin{array}{c}-\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{array}\right)}\)
これは、\(x\)軸の負の方向に1進んで、\(y\)軸の負の方向に1進む向きです。
上記の速度と加速度のベクトルの向きを、点Pを始点として描くと下図のようになります。
3.等速円運動の速度と加速度(微分無し)
先ほどの内容を、微分を用いずにみていきます。
\(\underline{\bf{○速度の大きさ}}\)
速さは、
\(\displaystyle{\bf{速さ=\frac{距離}{時間}}}\)
となります。
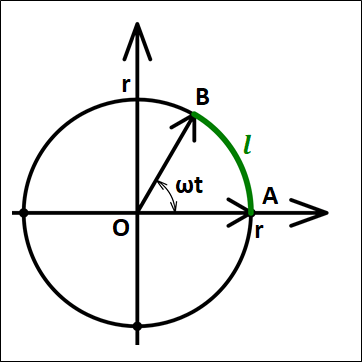
上図は、点\(A\)にいた物体が、\(t\)秒後に半径\(r\)の円周に沿って点\(B\)に移動した様子を表した図になります。
ここで、点が動いた距離は弧\(AB\)、すなわち図中の\(\textcolor{green}{l}\)となります。
この\(\textcolor{green}{l}\)は、角度が\(2\pi(=360°)\)に対して、\(\omega{t}\)分の円周(\(2\pi{r}\))になるので、
\(\displaystyle{\begin{eqnarray}\textcolor{green}{l}&=&2\pi{r}×\frac{\omega{t}}{2\pi}\\\\&=&r\omega{t}\end{eqnarray}}\)
これより速さは、距離を時間で割って、
\(\displaystyle{\begin{eqnarray}v&=&\frac{\textcolor{green}{l}}{t}\\\\&=&\frac{r\omega{t}}{t}\\\\&=&r\omega\end{eqnarray}}\)
となります。
\(\underline{\bf{○速度の向き}}\)
速度の定義は
\(\displaystyle{\vec{v}=\lim_{\Delta{t}\to0}\frac{\vec{r_{あと}}-\vec{r_{はじめ}}}{\Delta{t}}}\)
となります。
→変位・速度・加速度
よって、速度の大きさで見た図において、
\(\displaystyle{\vec{r_{はじめ}}=\overrightarrow{OA}}\)
\(\vec{r_{あと}}=\overrightarrow{OB}\)
となります。
そうすると、
\(\vec{r_{あと}}-\vec{r_{はじめ}}=\overrightarrow{AB}\)
となります。
→ベクトルの演算と成分表示
そして\(\Delta{t}\to0\)、すなわち\(\omega{t}\)という角度を限りなく\(0\)に近づけていくと、点\(A\)における速度ベクトルは点\(A\)における円の接線方向であることがわかります。
※
今
\(t_{はじめ}=0\)
\(t_{あと}=t\)
なので、
\(\Delta{t}=t-0=t\)
よって、\(\Delta{t}\to0\)と\(t\to0\)はおなじことを指している。
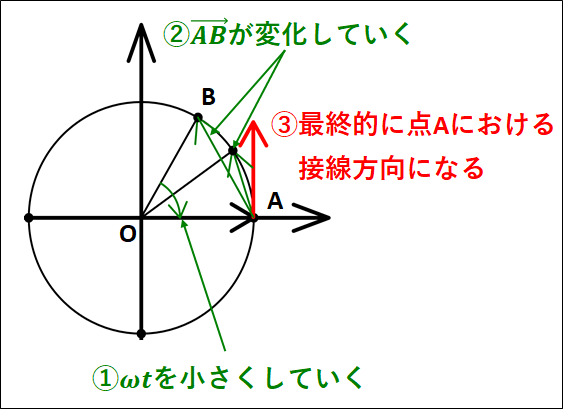
以上から、円運動の速度について
大きさ:\(r\omega\)
向き:接線方向
となります。
\(\underline{\bf{○加速度の大きさ}}\)
加速度の定義は
\(\displaystyle{\vec{a}=\lim_{\Delta{t}\to0}\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}}\)
となります。
また、速度ベクトルは円の接線方向でした。
よって、下図のようなベクトルを考えます。
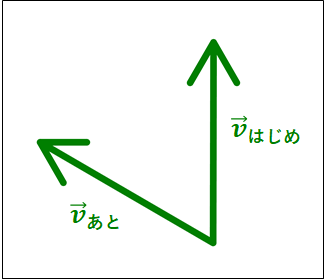
点\(A\)がはじめの位置、点\(B\)はあとの位置になります。
また、それぞれの位置における速度を\(\vec{v_{はじめ}}\)、\(\vec{v_{あと}}\)としています。
ベクトルは平行移動させてもよいので、速度ベクトルの始点を一致させてみます。
これらのなす角を求めるために、次の図を考えます。
図は円と速度ベクトルの始点を一致させた図を一緒に載せたものです。
また、\(\vec{v_{あと}}\)は見やすいように途中で切ってあります。
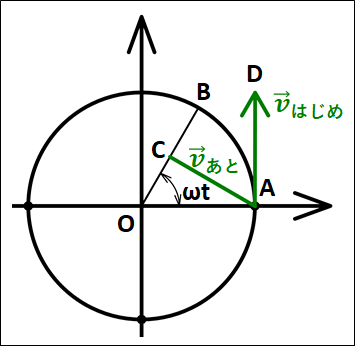
解説では、角度の単位\([rad]\)と\([°]\)が混じっています。
気になる方は、\(90°\)を\(\frac{\pi}{2}\)として考えてください。
点\(C\)は、\(OB\)と\(\vec{v_{あと}}\)との交点で、点\(D\)は\(\vec{v_{はじめ}}\)の始点です。
図から
\(\angle{B OA}=\omega{t}\)
となっています。
また、点\(B\)における速度が\(\vec{v_{あと}}\)であり、\(\vec{v_{あと}}\)は円の接線方向なので、\(OB\)と\(AC\)は直角です。
これより
\(\angle{OCA}=90°\)
よって、残った\(\angle{OAC}\)は\((90°-\omega{t})\)であると分かります。
次に、\(\vec{v_{はじめ}}\)は点\(A\)における接線方向なので
\(\angle{OA D}=90°\)
であり、また図から
\(\angle{O AD}=\angle{O AC}+\angle{C AD}\)
となります。
以上のことから、
\(\angle{O AD}=\angle{O AC}+\angle{C AD}\)
に
\(\angle{O AC}=(90°-\omega{t})\)
と
\(\angle{O AD}=90°\)
を代入して整理すると、
\(\displaystyle{\begin{eqnarray}&&\angle{O AD}=\angle{O AC}+\angle{C AD}\\\\{\Leftrightarrow}&&90°=90°-\omega{t}+\angle{C AD}\\\\{\Leftrightarrow}&&\angle{C AD}=\omega{t}\end{eqnarray}}\)
\(\angle{CAD}\)は\(\vec{v}_{はじめ}\)と\(\vec{v}_{あと}\)のなす角です。
よって、はじめとあとの速度ベクトルがなす角が\(\omega{t}\)であることが分かりました。
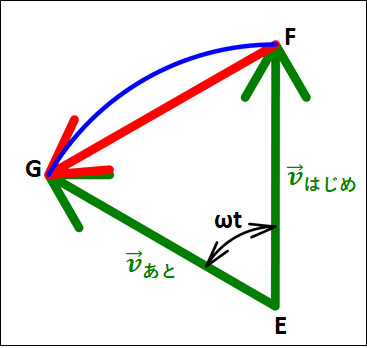
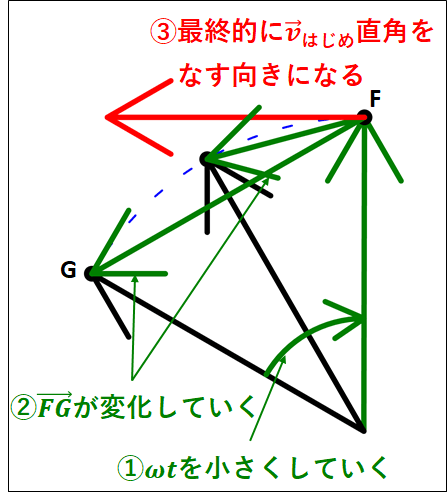
上図から、加速度の定義における\(\vec{v_{あと}}-\vec{v_{はじめ}}\)は赤色の\(\overrightarrow{FG}\)となります。
ここで、速度ベクトルの大きさは\(r\omega\)なので、速度の大きさを考えたときと同様に半径が\(r\omega\)の円における弧\(FG\)を考えると、
\(\displaystyle{\begin{eqnarray}\stackrel{\Large \frown}{FG}&=&2r\omega\pi×\frac{\omega{t}}{2\pi}\\\\&=&r{\omega}^2t\end{eqnarray}}\)
ここで、\(\Delta{t}\to0\)とすると弧\(FG\)と線分\(FG\)は限りなく等しくなってきます。
(長さの差が限りなく小さくなっていく)
これより、
\(\displaystyle{\begin{eqnarray}\Delta{v}&=&|\vec{v_{あと}}-\vec{v_{はじめ}}|\\\\&=&FG\\\\&≒&\stackrel{\Large \frown}{FG}\\\\&=&r{\omega}^2t\end{eqnarray}}\)
よって、加速度の大きさは
\(\displaystyle{\begin{eqnarray}|\vec{a}|&=&\frac{\Delta{v}}{\Delta{t}}\\\\&=&\frac{r{\omega}^2t}{t}\\\\&=&r{\omega}^2\end{eqnarray}}\)
また、速度の大きさ\(v=r\omega\)を用いると
\(\displaystyle{|\vec{a}|=r{\omega}^2=\frac{v^2}{r}}\)
となります。
\(\underline{\bf{○加速度の向き}}\)
\(\vec{a}\)の向きは\(\vec{v_{あと}}-\vec{v_{はじめ}}\)において\(\Delta{t}\)を限りなく\(0\)に近づけた際のベクトルの向きになります。
また、先ほどの図において、\(\vec{v_{あと}}-\vec{v_{はじめ}}\)は\(\vec{FG}\)となります。
よって、\(\omega{t}\)を限りなく\(0\)に近づけていくと、\(\vec{FG}\)は\(\vec{v_{はじめ}}\)と直角をなす向きになることが分かると思います。
この\(\vec{a}\)を円の点\(A\)が始点になるように図示すると、下図のようになります。
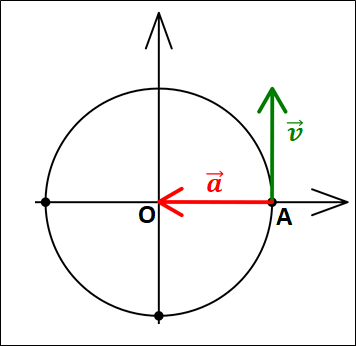
図から、\(\vec{a}\)は円の中心に向かう向きであることが分かります。
以上から、円運動の加速度について
大きさ:
\(\displaystyle{r{\omega}^2=\frac{v^2}{r}}\)
向き:円の中心方向
となります。
4.向心力
等速円運動をしている物体は、円の中心方向を正とした力を受けます。
この力を\(\textcolor{red}{\bf{向心力}}\)といいます。
等速円運動をしている物体について考える際には、向心力を見つけて運動方程式を立てることが重要となってきます。
※等速円運動をしている物体の加速度が円の中心向きだったので、運動方程式右辺の力も円の中心に向かう力(向心力)を正として立てる
5.慣性力と遠心力
\(\textcolor{red}{\bf{慣性力}}\)とは、"加速度運動をしている人(物体)が感じる\(\textcolor{red}{\bf{仮想的}}\)な力"のことです。
仮想的な力であるので、本来存在せず、作用・反作用の関係はありません。
\(\underline{\bf{○慣性力を用いる際の長所と短所}}\)

\(\bf{<証明>}\)
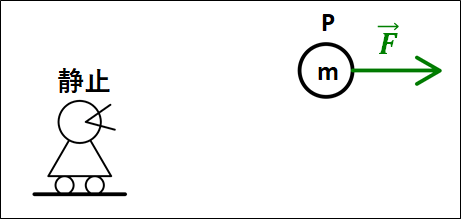
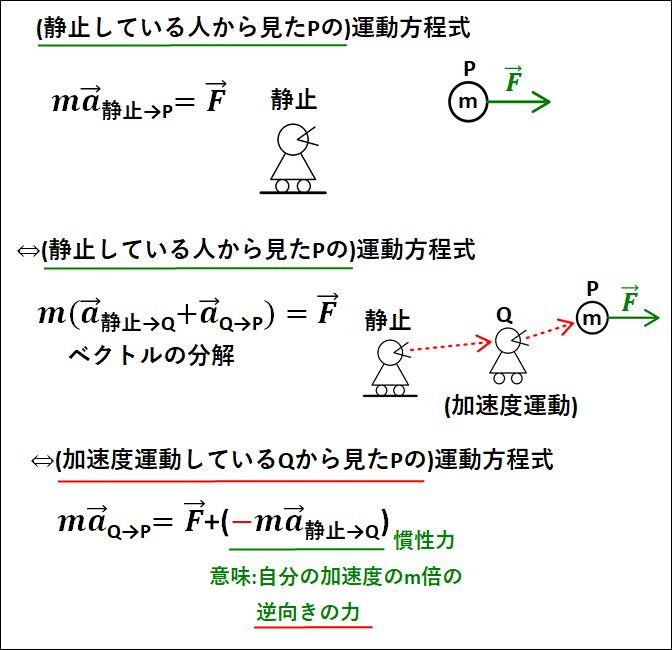
(静止している人から見た\(P\)の)運動方程式は
\(\displaystyle{m\vec{a}_{静止\to{P}}=\vec{F}}\)
この加速度ベクトルを下図のように分解します。
ベクトルの分解についてはこちら
→ベクトルの演算と成分表示
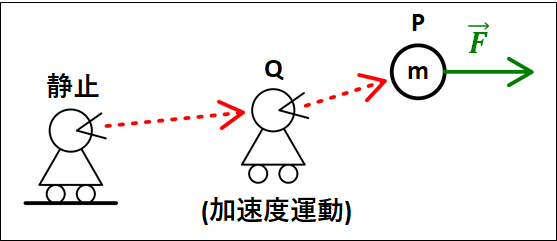
運動方程式は、
\(\displaystyle{m(\vec{a}_{静止\to{Q}}+\vec{a}_{Q\to{P}})=\vec{F}}\)
上式の\(m\vec{a}_{静止\to{Q}}\)を右辺に移項すると"(加速度運動している\(Q\)から見た\(P\)の)運動方程式"となります。
\(\displaystyle{m\vec{a}_{Q\to{P}}=\vec{F}-m\vec{a}_{静止\to{Q}}}\)
上式の\(-m\vec{a}_{静止\to{Q}}\)が慣性力となり、"自分(静止した人からみた加速度運動している人)の加速度の\(m\)倍で逆向きの力"となります。
下図にまとめておきます。
\(\underline{\bf{○遠心力}}\)
遠心力も慣性力です。
これは、円運動している物体と同じ円運動をしている人から見た慣性力となります。
遠心力は、円の中心から外向きにはたらきます。
遠心力も慣性力なのでみかけ上の(仮想的な)力となります。
6.円運動の式まとめ
○角速度\(\omega[rad/s]\)
→単位時間(1秒)あたり、何\(rad\)回転するか
\(t\)秒間では\(\omega{t}[rad]\)回転する。
この単位は、三角関数で扱う角度\(\theta\)と同じ単位。
○周期\(T[s]\)
→1回転するのに何秒かかるか
単位は便宜的に\(T[s/(回)]\)と考えるとわかりやすい。
\(\displaystyle{\bf{周期=\frac{円周}{速さ}}}\)
半径\(r\)の円の場合
\(\displaystyle{T[s]=\frac{2\pi{r}}{v}\left(=\frac{2\pi}{\omega}\right)}\)
(※\(v=r\omega\)を用いた)
周期の逆数\(n[/s]\) \((n[(回)/s])\) は、1秒間に何回転するかを表す。
\(\displaystyle{n[(回)/s]=\frac{1}{T[s/(回)]}}\)
また、単位[/s]は[Hz](ヘルツ)とも書く
※便宜的に単位に(回)をつけているだけで、実際の単位に(回)はつけない。
○円運動の速度の大きさと向き
・速度の大きさと角速度の関係
→\(v=r\omega\)
・速度の向き
→円の接線方向
○円運動の加速度の大きさと向き
・加速度の大きさ
\(\displaystyle{a=r{\omega}^2=\frac{v^2}{r}}\)
・加速度の向き
→円の中心方向
個人的に、角速度は問題文で単位と共に記載があると思うので、単位の意味がわかっていれば覚える必要は無いと思います。
周期と回転数については、意味を把握し、単位に(回)を補ってやるとわかりやすいです。
速度と加速度については、円周上の点を成分で表すことさえわかっていれば、あとは成分の微分とベクトルの大きさを計算すれば求めることができます。
慣れればそこまで時間はかからないですし、うろ覚えであった際の確認にも使えます。
11.運動量と力積
運動量と力積の関係は、運動方程式を変形していくことで導くことができます。
この記事では、上記の運動量と力積の関係や、二物体以上の運動方程式に関して内力化できる際に成り立つ運動量保存則について解説しています。
また、これらに関係する反発係数(はねかえり係数)についても載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.運動量と力積とは
力\(\vec{F}\)が働いている物体の運動方程式を考えます。
物体の質量を\(m\)とすると、運動方程式は、
\(\displaystyle{m\vec{a}=\vec{F} \cdots①}\)
ここで、加速度の定義式は、
\(\displaystyle{\vec{a}=\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}}\)
※加速度の定義についてはこちら
→変位・速度・加速度
なので、\(①\)の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&m\vec{a}=\vec{F}\\\\{\Leftrightarrow}&&m・\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}=\vec{F}\end{eqnarray}}\)
と書き換えられます。
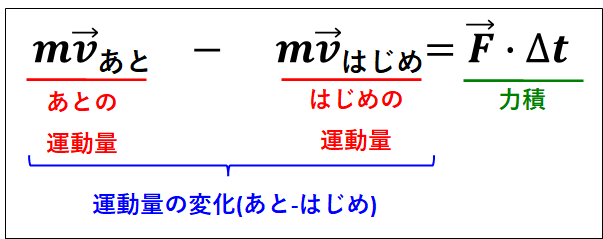
上式の両辺に\(\Delta{t}\)を掛けると
\(\displaystyle{\begin{eqnarray}&&m(\vec{v_{あと}}-\vec{v_{はじめ}})=\vec{F}・\Delta{t}\\\\{\Leftrightarrow}&&m\vec{v_{あと}}-m\vec{v_{はじめ}}=\vec{F}・\Delta{t} \cdots②\end{eqnarray}}\)
ここで、質量と速度の積\(\textcolor{red}{m・\vec{v}[kg・m/s]}\)を\(\textcolor{red}{\bf{運動量}}\)といい、力と作用時間の積\(\textcolor{red}{\vec{F}・\Delta{t}[N・s]}\)を\(\textcolor{red}{\bf{力積}}\)といいます。
\( (N・s=(kg・m/s^2)・s=kg・m/s\)となり、運動量と力積の単位は同じ)
運動量と力積のどちらも、向きと大きさをもつベクトルとなります。
以上から、式\(②\)の意味は以下のようになります。
上式は、"運動量の変化は、その間に受けた物体の力積に等しい"ことを表しています。
また、\(②\)式は成分でわけて考えることもできます。
\(\displaystyle{m\vec{v_{あと}}-m\vec{v_{はじめ}}=\vec{F}\Delta{t}}\)
↓成分で考えると
\(\displaystyle{\left\{\begin{array}{l}mv_{xあと}-mv_{xはじめ}=F_x\Delta{t} (x成分)\\\\mv_{yあと}-mv_{yはじめ}=F_y\Delta{t} (y成分)\end{array}\right.}\)
2.運動量保存則
運動量保存則は、下図の状況の際に使うことができます。

運動量保存則を考えるために、例として下記のような状況を考えます。
右向きに速さ\(v_{Aはじめ}\)で運動している物体\(A\)と、右向きに速さ\(v_{Bはじめ}\)で運動している物体\(B\)が衝突することを考えます。
衝突後、\(A,B\)はそれぞれ\(v_{Aあと} ,v_{Bあと}\) の速さで右向きに運動するとします。
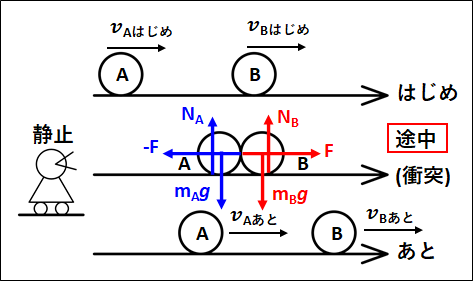
静止した人から見た\(\textcolor{red}{\bf{途中}}\)のつりあいと運動方程式を考えると、下図のようになります。
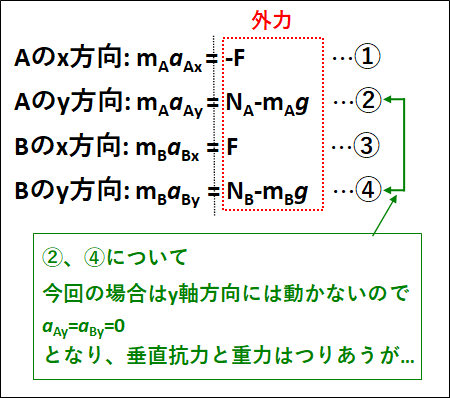
ここで、
○物体\(A,B\)の運動なので二体問題
○外力を内力化するために
の上記2つの事柄から、辺々を加えるという操作をします。
実際に、\(①+③\)から
\({m_A}{a_{Ax}}+{m_B}{a_{Bx}}=0\)
上記のように、"二体以上の運動方程式の辺々を足して外力がゼロになることを、\(\textcolor{red}{\bf{「外力が内力化された」}}\)といいます"
式変形を続けていくと、
\(\displaystyle{\begin{eqnarray}&&m_Aa_{Ax}+m_Ba_{Bx}=0\\\\{\Leftrightarrow}&&m_A\frac{v_{Aあと}-v_{Aはじめ}}{\Delta{t}}+m_B\frac{v_{Bあと}-v_{Bはじめ}}{\Delta{t}}=0\\\\{\Leftrightarrow}&&m_Av_{Aあと}+m_Bv_{Bあと}=m_Av_{Aはじめ}+m_Bv_{Bはじめ}\end{eqnarray}}\)
となります。
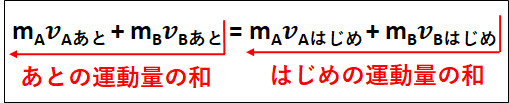
上式で表される法則を\(\textcolor{red}{\bf{運動量保存則}}\)といいます。
意味は、"複数の物体が内力を及ぼしあうだけで、外力を受けなければ(内力化できれば)これらの物体の運動量の総和は変化しない"というものになります。
今回の例では、\(x\)軸方向についてだけ運動量保存則が成り立ちますが、\(y\)軸方向についても内力化できるなら、\(y\)軸方向についても運動量保存則は成り立ちます。
\(\textcolor{red}{\bf{○ポイント}}\)
・いつ運動量保存則がつかえるのか?
→二体問題/内力化できる とき
・\(v\)は静止している人から見た値
(運動方程式は、静止した人からみて立てるから)
3.反発係数(はねかえり係数)
反発係数(はねかえり係数)\(e\)は、材質によって決まる物体同士のはねかえり度合いを表すものとなります。
反発係数\(e\)の定義は次のようになります。
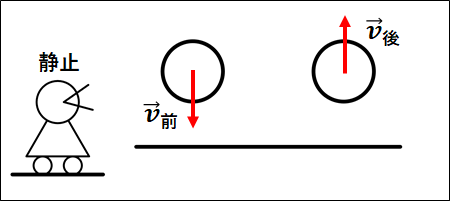
上図は、物体が地面にぶつかる前とぶつかった後の図になります。
ぶつかる前の速度を\(\vec{v}_{前}\)、ぶつかった後の速度を\(\vec{v}_{後}\)とすると、反発係数\(e\)は
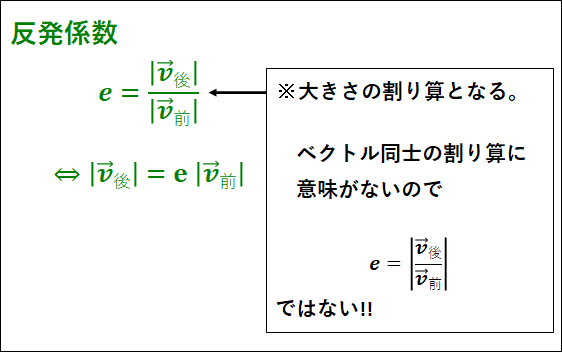
\(\displaystyle{\textcolor{green}{\begin{eqnarray}&&e=\frac{|\vec{v}_{後}|}{|\vec{v}_{前}|}\\\\{\Leftrightarrow}&&|\vec{v}_{後}|=e|\vec{v}_{前}|\end{eqnarray}}}\)
物体がなにかにぶつかると、その分エネルギーは損なわれてしまい、ぶつかる前の速さを超えることはありません。
なので、反発係数\(e\)の範囲は、
\(0{\le}e{\le}1\)
となります。
また、反発係数\(e\)の範囲が\(1\)以下であることを知っていれば、反発係数の定義において\(\vec{v}_{前}\)と\(\vec{v}_{後}\)のどちらが分母でどちらが分子か迷うことは無くなります。
基本的に\(\vec{v}_{前}\)の速さの方が大きいので、これが分子にきてしまうと\(e\)は\(1\)を超えてしまいます。
なので\(e\)が\(1\)を超えないように\(\vec{v_{前}}\)が分母で\(\vec{v_{後}}\)が分子となります。
また、速度(ベクトル)で表すと、
\(\displaystyle{\vec{v}_{後}=-\vec{v}_{前}}\)
となります。

上記が、反発係数\(e\)の定義となります。
また、反発係数はその値によって名称があります。
反発係数\(e\)の値は
\(0{\le}e{\le}1\)
となります。
(後の速さは前の速さより大きくはならない)
特に、
\(e=1\)のとき→\(\textcolor{green}{\bf{弾性衝突}}\)
\(0{\le}e{\lt}1\)のとき→\(\textcolor{green}{\bf{非弾性衝突}}\)
非弾性衝突の中でも、\(e=0\)のときを\(\textcolor{green}{\bf{完全非弾性衝突}}\)といいます。
4.二体問題における反発係数(はねかえり係数)
考える物体が一つの場合の反発係数については、記述しましたが、今回は二物体の場合の反発係数についてです。
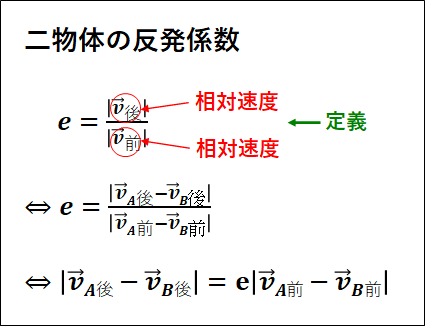
二物体の場合には、反発係数の定義における速度を、\(\textcolor{red}{\bf{相対速度}}\)で扱います。
物体\(A\)と物体\(B\)について、ぞれぞれの前の速度を\(\vec{v}_{A前} ,\vec{v}_{B前}\) 、それぞれの後の速度を\(\vec{v}_{A後} ,\vec{v}_{B後}\) とすると、下図のようになります。
また、速度(ベクトル)で表すと、
\(\displaystyle{\vec{v}_{A後}-\vec{v}_{B後}=\textcolor{red}{-}e(\vec{v}_{A前}-\vec{v}_{B前} )}\)
となります。
5.斜め衝突
下図のように、物体が滑らかな平面に斜めに衝突する場合を考えます。
(物体と床の間の反発係数を\(e\)とする)
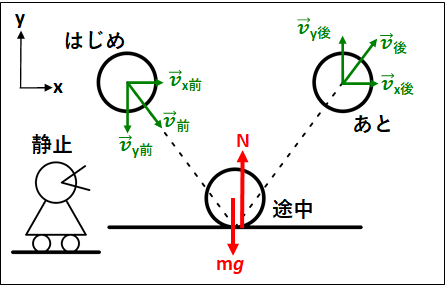
衝突前の速度を\(\vec{v}_{前}\)、衝突後の速度を\(\vec{v}_{後}\)とし、それぞれの速度は図のように\(x\)方向と\(y\)方向に分解してあります。
ここで、途中の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0\\ma_y=N-mg\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}m\frac{v_{x後} -v_{x前}}{\Delta{t}}=0 \cdots①\\m\frac{v_{y後} -v_{y前}}{\Delta{t}}=N-mg \cdots②\end{array}\right.\end{eqnarray}}\)
上式から、\(x\)方向の速度については\(①\)から
\(v_{x後}=v_{y前}\)
であると分かります。
しかしながら、\(y\)軸方向の速度については、\(②\)式から得られる情報はありません。
運動方程式からは\(y\)軸方向の速度がわかりませんが、反発係数を用いると、
\(\displaystyle{\begin{eqnarray}&&e=\frac{|v_{y後}|}{|v_{y前}|}\\\\{\Leftrightarrow}&&|v_{y後}|=e|v_{y前}|\\\\{\Leftrightarrow}&&v_{y後}=-ev_{y前}\end{eqnarray}}\)
となり、\(y\)軸方向の速度について情報を得ることができます。
6.衝突と力学的エネルギーの損失
反発係数の値によって、エネルギーは保存されたり失われたりします。
○弾性衝突(\(e=1\))のとき
力学的エネルギーは失われずに、保存される。
一つの物体の場合、力学的エネルギーが保存されるので、前と後の速さは同じになる。
○非弾性衝突(\(0{\le}e{\lt}1\))のとき
力学的エネルギーは減少し、失われた力学的エネルギーは熱や音、物体の変形に使われる。
一つの物体の場合、力学的エネルギーは減少してしまうので、前の速さよりも後の速さの方が小さくなる。
こちらの具体的な計算については、練習問題で扱います。
10.仕事とエネルギー
こちらの記事は、仕事とエネルギーについて解説しています。
仕事については、仕事の定義や仕事とエネルギーの等価性について解説しています。
またエネルギーについては、運動エネルギーや各種位置エネルギー、力学的エネルギーについて解説しています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
- 1.仕事の定義
- 2.仕事の原理
- 3.仕事率
- 4.運動エネルギーと仕事の関係
- 5.重力による位置エネルギー
- 6.弾性力による位置エネルギー
- 7.保存力と非保存力
- 8.力学的エネルギー保存の法則
- 9.非保存力と力学的エネルギー
1.仕事の定義
物理における仕事の定義は、以下のようになります。
物体に力\(\vec{F}[N]\)を加え、距離\(\vec{S}[m]\)だけ移動させたとき、力\(\vec{F}\)が物体にした仕事\(W\)は、\(\vec{F}\)と\(\vec{S}\)の内積
\(\displaystyle{W=\vec{F}・\vec{S}}\)
で表されます。
また、\(\vec{F}\)と\(\vec{S}\)のなす角を\(\theta\)とすると、\(\vec{F}\)と\(\vec{S}\)の大きさ\(|\vec{F}|\)と\(|\vec{S}|\)を用いて
\(\displaystyle{\begin{eqnarray}W&=&\vec{F}・\vec{S}\\\\&=&|\vec{F}||\vec{S}|\cos\theta\end{eqnarray}}\)
とかけます。
仕事の定義式の右辺は、"(大きさ)×(大きさ)"なので、仕事はベクトルではありません。
ベクトルの内積についてはこちらも参考にしてください。
→ベクトルの内積と外積
仕事\(W\)の単位は、力\([N]\)と距離\([m]\)を掛けているので
\(N×m=N・m\)
となります。
また、\(N・m\)は別の単位でも表すことができ、この単位を\([J]\)(ジュール)といいます(新しい単位)。
\(\displaystyle{\begin{eqnarray}N・m=J\end{eqnarray}}\)
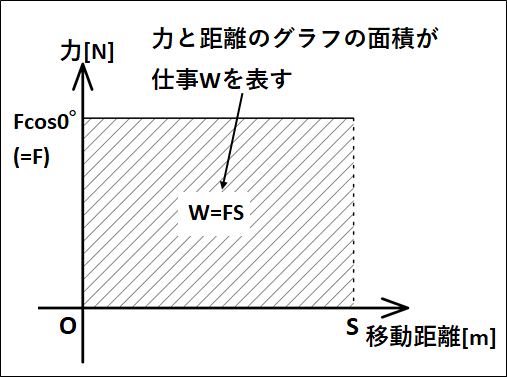
仕事は、力\(F\)と距離\(S\)のグラフの面積に相当します。
例として、下図のように物体に力\(\vec{F}[N]\)を右向きに加えて距離\(\vec{S}[m]\)だけ右向きに動かしたときに、力\(\vec{F}\)が物体にした仕事を考えてみます。
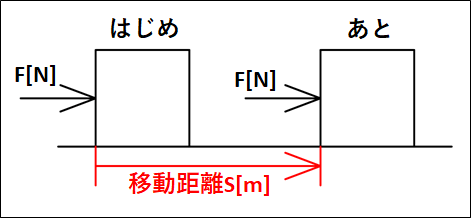
上図において、\(\vec{F}\)と\(\vec{S}\)のなす角は\(0°\)です。
また、それぞれのベクトルの大きさは\(F\)と\(S\)になります。
よって、力\(F\)が物体にする仕事\(W\)は
\(\displaystyle{\begin{eqnarray}W&=&\vec{F}・\vec{S}\\\\&=&F×S×\cos{0°}\\\\&=&FS\end{eqnarray}}\)
となります。
このときグラフは下図のようになります。
一般に、物体がいくつかの力を受けて移動する場合、それぞれの力がする仕事の和はそれらの合力がする仕事に等しくなります。
2.仕事の原理
仕事の原理とは、道具を用いて仕事をするとき、道具の質量や摩擦が無視できれば、仕事の量は道具を用いないときと変わらないという原理になります。
こちらについては、練習問題のほうで実際に問題を解きながら解説します。
3.仕事率
仕事率とは、単位時間(\(1s\))あたりにする仕事の値になります。
\(t[s]\)間の間に\(W[J]\)の仕事をするときの仕事率を\(P\)とすると、
\(\displaystyle{\begin{eqnarray}P=\frac{W[J]}{t[s]}\end{eqnarray}}\)
となります。
仕事率の単位は、仕事の単位\(J\)を時間の単位\(s\)で割っているので、\(J/s\)となります。
また、この単位\(J/s\)を別の単位\(W\)(ワット)で表すこともあります。
\(\displaystyle{J/s=W}\)
記号は\(W\)と、この記事における仕事と同じ文字になっていますが、混同しないようにしてください。
\(\bf{<考察>}\)
仕事の単位\(J\)は、力の単位\(N\)と距離の単位\(m\)を用いて、
\(J=N・m\)
と表されました。
この単位を用いて、仕事率を考えてみると
\(\displaystyle{\begin{eqnarray}{\bf{仕事率}}([W=J/s])&=&\frac{\bf{仕事[J]}}{\bf{時間[s]}}\\\\&=&\frac{\bf{力[N]}×距離[m]}{時間[s]}\end{eqnarray}}\)
ここで、分子の距離\(m\)と分母の時間\(s\)に注目すると、これは
\(\displaystyle{\frac{距離[m]}{時間[s]}=速さ[m/s]}\)
となります。
これを用いると、仕事率は下記のようにも表すことができます。
\(\displaystyle{\begin{eqnarray}{\bf{仕事率}}([W=J/s])&=&\frac{\bf{仕事[J]}}{\bf{時間[s]}}\\\\&=&\frac{\bf{力[N]}×距離[m]}{時間[s]}\\\\&=&\textcolor{red}{\bf{力[N]×速さ[m/s]}}\end{eqnarray}}\)

4.運動エネルギーと仕事の関係
物体が仕事をする能力をもっているとき、この物体は"エネルギーをもつ"といいます。
運動する物体がもつ仕事する能力を\(\textcolor{red}{\bf{運動エネルギー}}\)といい、質量\(m[kg]\)の物体が速さ\(v[m/s]\)で運動しているときの運動エネルギー\(K\)は、
\(\displaystyle{K=\frac{1}{2}mv^2}\)
で表されます。
単位は、\(N=kg・m/s^2\)なので
\(\displaystyle{\begin{eqnarray}kg×(m/s)^2&=&kg・m/s^2×m\\\\&=&N・m\\\\&=&J\end{eqnarray}}\)
のように、(J)(ジュール)となり、仕事の単位と同じになります。
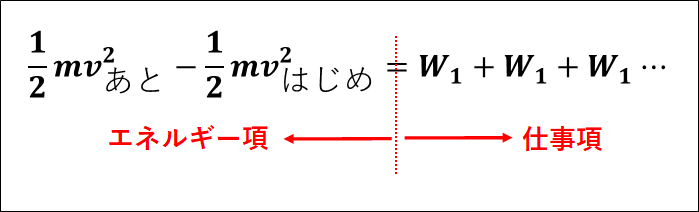
また、物体の運動エネルギーと物体にはたらいている力がした仕事の間には、以下のような関係があります。
\(\displaystyle{\textcolor{red}{\frac{1}{2}mv^2_{あと}-\frac{1}{2}mv^2_{はじめ}=W_1+W_2+W_3+\cdots}}\)
\(v_{あと}\)は物体のあとの速度、\(v_{はじめ}\)は物体のはじめの速度となります。
上記の式の右辺は、運動エネルギーの(あと-はじめ)、すなわち運動エネルギーの変化量を表しています。
上式の右辺は、物体にはたらいている力がした仕事の和になります。
これを、言葉で表すと
(運動エネルギーの変化量)=(仕事の和)
となります。
これを、
\(\textcolor{red}{\bf{運動エネルギーと仕事の(等価性)原理}}\)
といいます。
上式は、\(\textcolor{red}{\bf{覚えておく必要があります}}\)。
"運動エネルギーと仕事の原理"を考えるために、複数の力がかかっている物体を考えます。
少しだけ微積を用いるので、興味がない方は飛ばしてもらってもかまいませんが、上式の"運動エネルギーと仕事の原理"の式は覚えておきましょう。
力は、3つだけ図示してありますが、複数かかっているとしています。
また、この力がはたらいている状態で初速度\(v_{はじめ}\)を物体に与え、\(\vec{r}\)だけ移動したあとの物体の速度を\(v_{あと}\)としています。
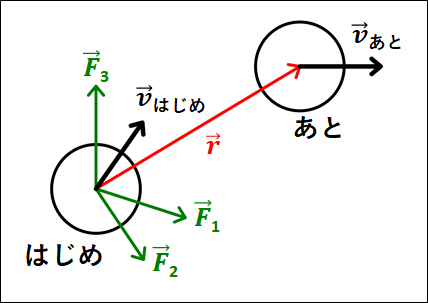
上図の状態において、物体の運動方程式は、
\(\displaystyle{m\vec{a}=\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots}\)
となります。
上記の運動方程式の両辺に\(\vec{v}\)を内積して、計算していくと下図のようになります。

仕事率の部分で考察したように、(力×速度)は仕事率となります。
次に、合成関数の微分法を用いて、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}v^2&=&\frac{dv^2}{dv}\frac{dv}{dt}\\\\&=&2v\frac{dv}{dt}\end{eqnarray}}\)
から、
\(\displaystyle{v\frac{dv}{dt}=\frac{d}{dt}\frac{1}{2}v^2}\)
※合成関数の微分については、こちらを参考にしてください。
→微分法とその応用
これを用いて、式変形を続けていくと、

以上より、上式の分子\(d\left\{\right\}\)のみを考えると、\(\textcolor{red}{d}\)は\(\textcolor{red}{\bf{あと-はじめ}}\)という意味なので、
\(\displaystyle{\frac{1}{2}mv^2_{あと}-\frac{1}{2}mv^2_{はじめ}=W_1+W_2+W_3+\cdots}\)
となります。
はじめの位置では、物体は移動していないのではじめの仕事はすべてゼロとなります。
また、\(\vec{v}\)は2乗されているので、これはベクトルではなくベクトルの"大きさ"となります。
ここで、もう一度"運動エネルギーと仕事の原理"の式の意味を確認しておきます。

上式は、
"物体の運動エネルギーの変化は、その物体がされた仕事に等しい"
ことを示しています。
また、左辺を"エネルギー項"、右辺を"仕事項"といいます。
また、エネルギー積分についても触れておきます。
これは、電磁気の分野でも扱います。
\(\bf{\underline{○エネルギー積 分}}\)
直線上の運動(今回は\(x\)軸上)を考えます。
運動方程式は、
\(\displaystyle{ma=F}\)
両辺に\(v\)を掛けて
\(\displaystyle{\begin{eqnarray}&&mv a=Fv\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=F\frac{dx}{dt} \left(∵a=\frac{dv}{dt} , v=\frac{dx}{dt}\right)\end{eqnarray}}\)
ここで、両辺\(t\)で\(t_{はじめ}{\to}t_{あと}\)まで積分して、
\(\displaystyle{\int_{t_{はじめ}}^{t{あと}}{mv\frac{dv}{dt}}dt=\int_{t_{はじめ}}^{t{あと}}{F\frac{dx}{dt}}dt}\)
\(x\)と\(v\)は\(t\)の関数なので、\(t_{はじめ}{\to}t_{あと}\)のとき\(x_{はじめ}{\to}x_{あと}\)、\(v_{はじめ}{\to}v_{あと}\)であるとすると、
\(\displaystyle{\begin{eqnarray}&&\int_{v_{はじめ}}^{v_{あと}}{mv}dv=\int_{x_{はじめ}}^{x_{あと}}{F}dx\\\\{\Leftrightarrow}&&\left[\frac{1}{2}mv^2\right]_{v_{はじめ}}^{v_{あと}}=\int_{x_{はじめ}}^{x_{あと}}{F}dx\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\int_{x_{はじめ}}^{x_{あと}}{F}dx\end{eqnarray}}\)
となります。

5.重力による位置エネルギー
物体に重力がはたらいているとき、重力がした仕事を\(W_{mg}\)とすると、運動エネルギーと仕事の等価性から、
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\textcolor{green}{W_{mg}}}\)
となります。
上式のおいて、重力がした仕事\(W_{mg}\)をエネルギー項である左辺に移項したもの、つまり\(-W_{mg}\)が"重力による位置エネルギーの変化量"となります。
位置エネルギーにも、運動エネルギーと同様に"はじめの位置エネルギー"と"あとの位置エネルギー"があります。
なので、位置エネルギーの変化量だけを扱う場合には\(-W_{mg}\)を用いればよいですが、"はじめの重力による位置エネルギー"と"あとの重力による位置エネルギー"をそれぞれ扱う場合には、\(\textcolor{green}{\bf{基準面}}\)を決めて、\(\textcolor{green}{\bf{座標}}\)で考える必要があります。
例をみていきましょう。
例)
基準面\(O\)から高さ\(h\)だけ高い位置\(P\)にある質量\(m\)の物体を静かに落とした場合について。
状況は下図のようになります。
"高さ"といわれたときには、上向きを正とします。
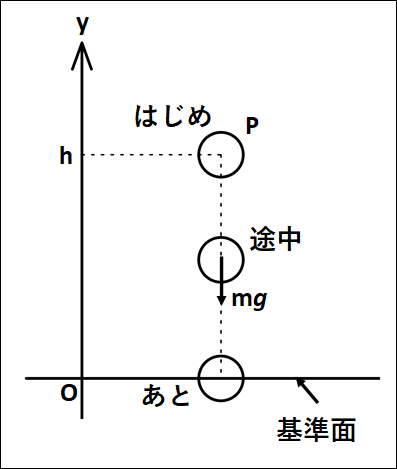
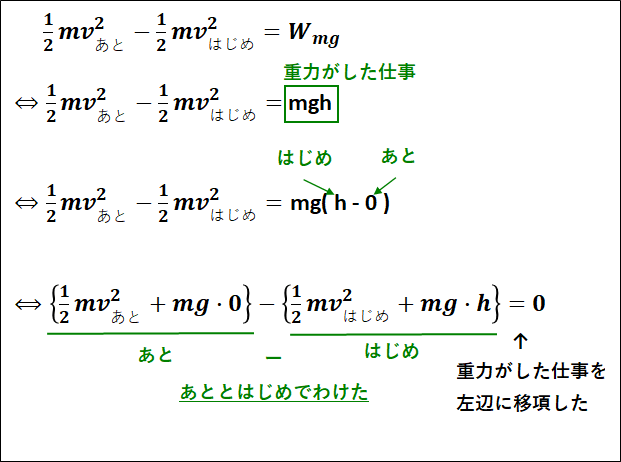
物体が\(P\)から\(O\)まで移動するとき、運動エネルギーと仕事の等価性から
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_{mg}}\)
ここで、重力は鉛直下向きに大きさ\(mg\)で、移動距離は下向きに\(h\)だけ移動しています。
この重力と移動距離のベクトルのなす角は\(0°\)となるので、重力がした仕事は
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×h×\cos{0°}\\\\&=&mgh\end{eqnarray}}\)
となります。
また、これを座標で捉えると、
\(\displaystyle{mgh=mg(h-0)}\)
となります。
これらを用いて、式を変形していくと下図のようになります。
上式において、

運動エネルギーを\(K\)と表しましたが、位置エネルギーは\(U\)と表します。
上式の結果から、基準面から高さ\(h\)だけ高い位置にある物体の重力による位置エネルギー\(U\)は\(mgh\)となります。
(はじめ(点P)の重力による位置エネルギー)
(基準面にある物体の重力による位置エネルギーは\(0\))
※
重力がする仕事について、途中の運動方程式を考えると上向きを正としているので
\(ma=-mg\)
これより、重力と距離のグラフを考えると、その面積が重力がした仕事となるので下図のようになります。
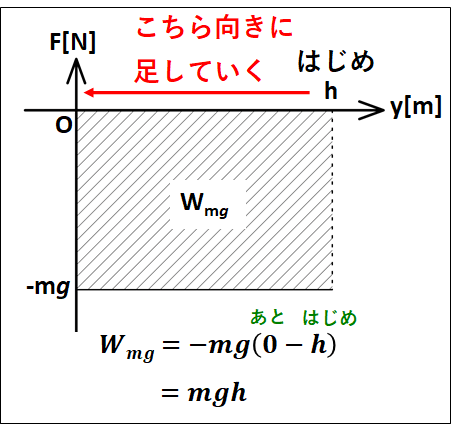
物理においては、面積の符合も意味をもつので、力の正負や足していく向きも考える必要があります。
これを積分で表すと、
\(\displaystyle{\begin{eqnarray}\int_h^0{(-mg)}dy&=&\left[-mgy\right]_h^0\\\\&=&-mg・0-(-mg)・h\\\\&=&mgh\end{eqnarray}}\)
となります。
また、重力がした仕事は物体の移動経路が曲線や斜めの場合でも、重力の大きさと物体が鉛直方向に動いた距離で決まります。
このことについては、練習問題で取り扱います。
6.弾性力による位置エネルギー
物体に弾性力がはたらいているとき、弾性力がした仕事を\(W_{s}\)とすると、運動エネルギーと仕事の等価性から、
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\textcolor{green}{W_{s}}}\)
となります。
上式のおいて、弾性力がした仕事\(W_{s}\)をエネルギー項である左辺に移項したもの、つまり\(-W_{s}\)が"弾性力による位置エネルギーの変化量"となります。
こちらも重力による位置エネルギーと同様に、"はじめの位置エネルギー"と"あとの位置エネルギー"を考える際には、座標を用います。
例をみていきます。
例)
自然長の位置を原点として、原点から\(L[m]\)だけ伸びたバネにつながれた物体が、自然長にもどるときを考える。
(ばね定数を\(k\)とし、ばねが伸びる方向に\(x\)軸をとる)
床はなめらかであるとします。
状況は下図のようになります。
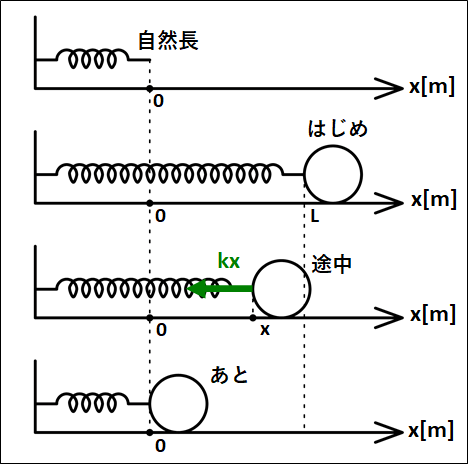
途中での物体の位置を\(x\)としています。
物体が運動している途中での運動方程式は、軸を右向き正にとっているので、ばねによる弾性力が負の方向にかかっていることから、
\(ma=-kx\)
これをもとにして、弾性力と位置のグラフを描くと次のようになります。
グラフと一緒に、自然長、はじめの位置、あとの位置の物体も一緒に載せておきます。
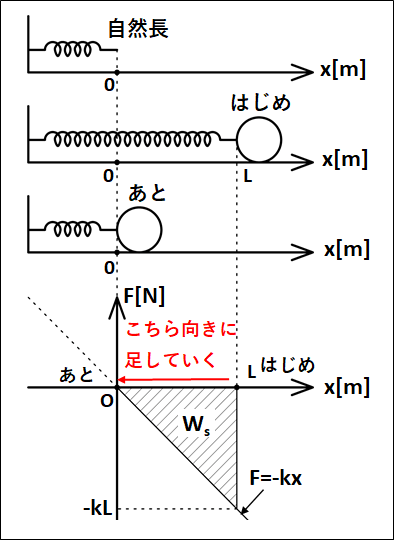
グラフの面積が、弾性力のした仕事なので、三角形の面積を求める式から、
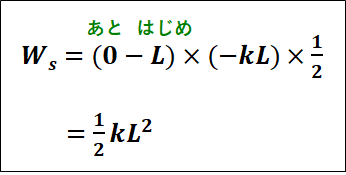
※
積分を用いると、
\(\displaystyle{\begin{eqnarray}\int_L^0{(-kx)}dx&=&\left[-\frac{1}{2}lx^2\right]_L^0\\\\&=&-\frac{1}{2}k・0^2-\left(-\frac{1}{2}kL^2\right)\\\\&=&\frac{1}{2}kL^2\end{eqnarray}}\)
となります。
以上より、ばねの弾性力がした仕事が求まったので、重力による位置エネルギーのときと同様にして、運動エネルギーと仕事の原理から、式変形をしていくと下図のようになります。
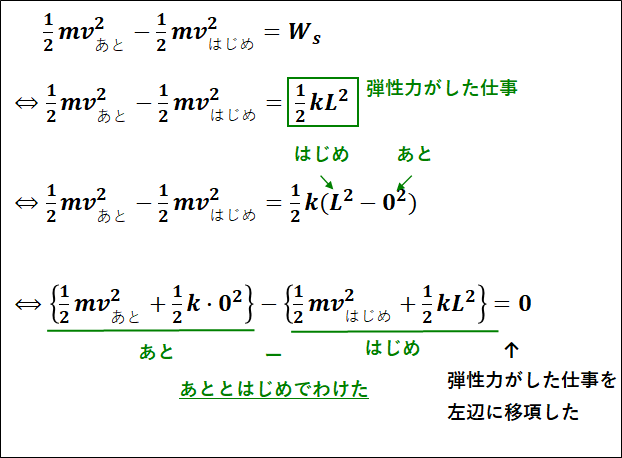
上式において、

上式の結果から、自然長から\(L\)だけ伸びたばねの弾性力による位置エネルギー\(U\)は、ばねの自然長の位置を基準にとると
\(\displaystyle{U=\frac{1}{2}kL^2}\)
となります。
(はじめの弾性力による位置エネルギー)
(自然長でのばねの弾性力による位置エネルギーは\(0\))
7.保存力と非保存力
\(\textcolor{red}{\bf{保存力}}\)とは、"力がする仕事が途中の経路によらず、はじめとあとの2点(はじめの位置とあとの位置)だけで決まる力"のこととなります。
\(\textcolor{red}{\underline{\bf{○代表的な保存力:}}}\)
\(\textcolor{red}{\bf{重力、万有 引力、弾性力、静電気力(クーロン 力)}}\)
\(\textcolor{red}{\bf{非保存力}}\)とは、"力がする仕事が、はじめとあとの位置だけでは決まらずに、経路によるもの"となります。
例としては、摩擦力や空気抵抗などがあります。
"保存力"と"非保存力"については、"保存力"を覚えておきましょう。
保存力でないものは、非保存力となります。
また、運動エネルギーと仕事の等価性原理の式から、仕事を仕事項からエネルギー項へ移項した際に「○○による位置エネルギー」となるのは"保存力"のみとなります。
(非保存力は、移行させても位置エネルギーにならない(はじめとあとだけで決まらない))
保存力と非保存力の例として、重力と摩擦力を比較してみます。
例)
\(\bf{\underline{保存力:重力}}\)
質量\(m\)の物体が下図のように、\(A→B→C\)と移動するときの重力がした仕事を考えます。
\(A\)点を基準として、\(A\)から\(B\)までの距離を\(l_1\)、\(A\)から\(C\)までの距離を\(l_2\)とします。
重力\(mg\)は常に鉛直下向きにかかっています。
\(\bf{\underline{・A→B間}}\)
上向きに\(l_1\)だけ移動します。
よって、重力とはなす角が\(180°\)になるので、この間に重力がした仕事は
\(\displaystyle{mg×l_1×\cos{180°}=-mgl_1}\)
\(\bf{\underline{・B→C間}}\)
下向きに\((l_1-l_2)\)だけ移動します。
重力とのなす角は\(0°\)なので、この間に重力がした仕事は
\(\displaystyle{mg×(l_1-l_2)×\cos{0°}=mg(l_1-l_2)}\)
\(\bf{\underline{・全体でした仕事}}\)
全体でした仕事は、\(A→B\)の間にした仕事と\(B→C\)の間にした仕事を足して、
\(\displaystyle{\begin{eqnarray}-mgl_1+mg(l_1-l_2)&=&-mg(l_1-l_1+l_2)\\\\&=&-mg(l_2-0)\end{eqnarray}}\)
これより、保存力である重力がした仕事は、はじめの位置である\(0\)とあとの位置である\(l_2\)のみで決まり、途中の位置\(l_1\)は関係ないことが分かります。

例)
\(\bf{\underline{非保存力:摩擦力}}\)
物体が下図のように、\(A→B→C\)と移動するときの摩擦力がした仕事を考えます。
\(A\)点を基準として、\(A\)から\(B\)までの距離を\(l_1\)、\(A\)から\(C\)までの距離を\(l_2\)とします。
かかっている動摩擦力の大きさを\(f\)とします。
この摩擦力は、"物体が運動する向きと反対向き"にはたらきます。
\(\bf{\underline{・A→B間}}\)
右向きに\(l_1\)だけ移動します。
摩擦力\(f\)は物体が運動する向きと逆向きの左向きにかかります。
よって、2つのベクトルのなす角は\(180°\)となるので、この間で摩擦力がした仕事は
\(\displaystyle{f×l_1×\cos{180°}=-fl_1}\)
\(\bf{\underline{・B→C間}}\)
左向きに\((l_1-l_2)\)だけ移動します。
摩擦力\(f\)は物体が運動する向きと逆向きの右向きにかかります。
よって、2つのベクトルのなす角は\(180°\)となるので、この間で摩擦力がした仕事は
\(\displaystyle{f×(l_1-l_2)×\cos{180°}=-f(l_1-l_2)}\)
\(\bf{\underline{・全体でした仕事}}\)
全体でした仕事は、\(A→B\)の間にした仕事と\(B→C\)の間にした仕事を足して、
\(\displaystyle{\begin{eqnarray}-fl_1-f(l_1-l_2)&=&-f(l_1+l_1-l_2)\\\\&=&-f(2l_1-l_2)\end{eqnarray}}\)
上式から、非保存力である摩擦力がした仕事は、はじめとあとの位置だけでは決まらず、途中の位置も考えなければならないことがわかります。

8.力学的エネルギー保存の法則
\(\textcolor{red}{力学的エネルギー}\)とは、"運動エネルギーと位置エネルギーの和"のことです。
すなわち、運動エネルギーを\(K\)、位置エネルギーを\(U\)とすると、
\(\textcolor{red}{{\bf{力学的エネルギー}}=K+U}\)
となります。
\(\textcolor{red}{\bf{力学的エネルギー保存の 法則}}\)とは、
"物体が保存力\(\textcolor{red}{\bf{だけ}}\)から\(\textcolor{green}{\bf{仕事}}\)をされるとき、運動エネルギーと位置エネルギーの和である力学的エネルギーは保存される"
という法則です。
保存するとは、"はじめの力学的エネルギー"と"あとの力学的エネルギー"が等しいということです。
また言い換えると、力学的エネルギーの変化量が"ゼロ"だということです。
式で表すと、運動エネルギーを\(K\)、位置エネルギーを\(U\)、変化量を表す\(\Delta\)を用いると
\(\displaystyle{\begin{eqnarray}&&(K_{あと}+U_{あと})=(K_{はじめ}+U_{はじめ})\\\\{\Leftrightarrow}&&(K_{あと}+U_{あと})-(K_{はじめ}+U_{はじめ})=0\\\\{\Leftrightarrow}&&\Delta(K+U)=0\end{eqnarray}}\)
となります。
ただし、これが成り立つのは"物体が保存力だけから仕事をされるとき"という条件が必要となります。
(非保存力による仕事は、エネルギー項に移項させても位置エネルギーとはならない)
"保存力だけから仕事をされるとき"なので、物体に非保存力がはたらいていても、その非保存力がした仕事が"ゼロ"であれば"力学的エネルギー保存の法則"は成り立ちます。
(個人的には、力学的エネルギーの法則は、運動エネルギーと仕事のと原理から自然に導かれるので、覚える必要はないと思いますが…)
これから、いくつか例をみていきます。
例1)
なめらかな斜面上を、斜面に沿って高さ\(h_A\)から\(h_B\)まで滑り降りる質量\(m\)の物体
状況は下図のようになります。
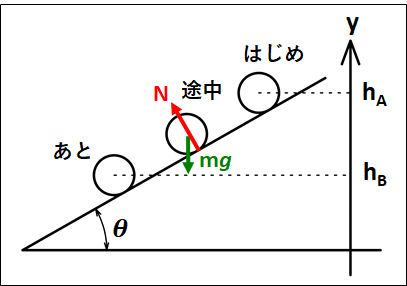
途中でかかっている力は、鉛直下向きに重力\(mg\)と、斜面と直角に垂直抗力\(N\)がかかっています。
運動エネルギーと仕事の原理から、重力がした仕事を\(W_{mg}\)、垂直抗力がした仕事を\(W_{N}\)とすると、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_{mg}+W_{N}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(h_A-h_B)+N×\frac{h_A-h_B}{\sin\theta}\cos{90°}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(h_A-h_B)+0\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式のように、物体に非保存力である垂直抗力がはたらいていますが、その仕事は"ゼロ"となっているので、力学的エネルギーは保存しています。
※重力がした仕事、\(W_{mg}=mg(h_A-h_B)\)に関して、下図を考えます。
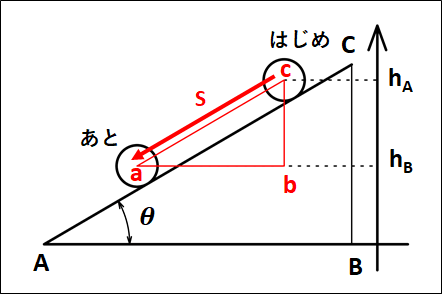
下図において、物体が移動した距離を\(s\)としています。
物体は、斜面に沿って移動するので、
\(AC//ac\)
です。
また、\(ac\)を斜辺とする直角三角形を考えているので、
\(AB//ab\)、\(BC//bc\)
です。
これより、
\(\angle{BAC}=\angle{bac}=\theta\)
\(\angle{ABC}=\angle{abc}=90°\)
\(\angle{ACB}=\angle{acb}=90°-\theta\)
となり、下図のようになります。
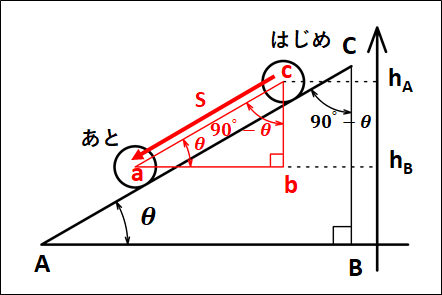
ここで、重力がした仕事は仕事の定義から
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×s×\cos(90°-\theta)\\\\&=&mg×s×\sin\theta\end{eqnarray}}\)
三角関数から、\(s\sin\theta\)は\(h_A-h_B\)なので、重力がした仕事は
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×s×\sin\theta\\\\&=&mg(h_A-h_B)\end{eqnarray}}\)
となります。
※三角関数についてはこちら
→三角関数の定義と関係式
→三角関数の公式
一般的に、重力がした仕事は重力の大きさと高さだけで決まってきます。
これについては、練習問題で詳しく扱っています。
例2)
なめらかな平面上で、ばねにつながれた質量\(m\)の物体が自然長からの伸び\(x_A\)から\(x_B\)まで移動するとき。
ばね定数を\(k\)とする。
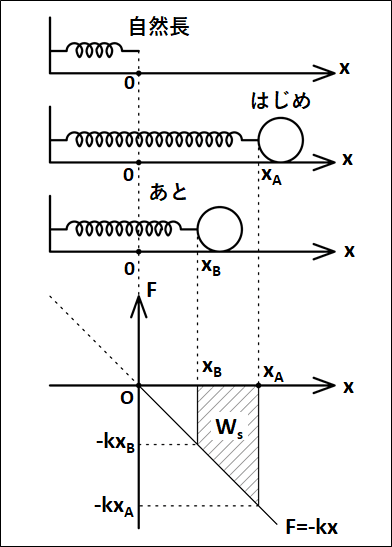
途中でかかっている力は、以下のようになります。
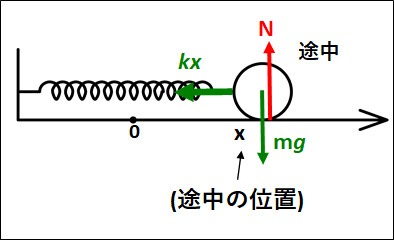
かかっている力は、重力\(mg\)と垂直抗力\(N\)と弾性力\(kx\)になります。
なので、仕事もこれら3つの力による仕事を考えなけばなりません。
弾性力による仕事\(W_s\)についてですが、上図の面積となるので、あとの負の面積(小さい三角形)からはじめの負の面積(大きい三角形)を引いて
\(\displaystyle{\begin{eqnarray}W_s&=&-\frac{1}{2}kx_B^2-\left\{-\frac{1}{2}kx_A^2\right\}\\\\&=&\frac{1}{2}k(x_A^2-x_B^2)\end{eqnarray}}\)
※
積分表示は\(\displaystyle{\int_{x_A}^{x_B}{-kx}dx}\)
以上から、弾性力による仕事を\(W_s\)、垂直抗力による仕事を\(W_N\)、重力による仕事を\(W_{mg}\)とすると、これまでと同様に運動エネルギーと仕事の原理から
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_s+S_N+W_{mg}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(x_A^2-x_B^2)+N(x_A-x_B)\cos{90°}\\&& +mg(x_A-x_B)\cos{90°}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(x_A^2-x_B^2)+0+0\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式より、力学的エネルギーである"運動エネルギー"と"弾性力による位置エネルギー"の和は保存しています。
例3)
ばねで吊り下げられた質量\(m\)の物体が、自然長からの伸びが\(y_A\)から\(y_B\)まで移動するとき。
ばね定数を\(k\)とする。
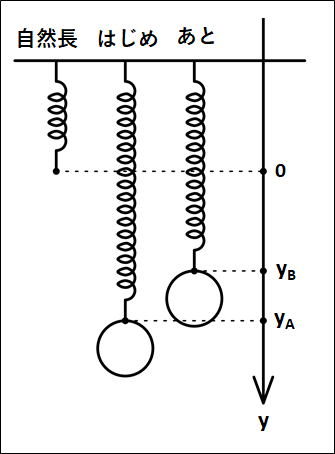
途中の位置\(y\)でかかっている力は、以下のようになります。
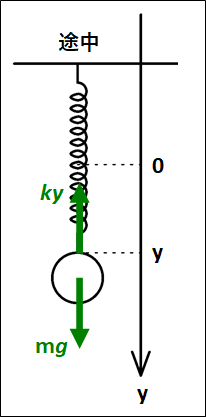
今回は、自然長の位置を原点としていますが、つりあいの位置を原点にすることもあります。
(特に、単振動の分野で)
物体にかかっている力は、鉛直下向きに重力\(mg\)と鉛直上向きに弾性力\(ky\)、また進んだ距離は上向きに\(y_A-y_B\)となります。
以上から、これまでと同様に運動エネルギーと仕事の原理から、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_s+W_{mg}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(y_A^2-y_B^2)-mg(y_A-y_B)\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式より、力学的エネルギーである"運動エネルギー"と"弾性力による位置エネルギー"と"重力による位置エネルギー"の和は保存しています。
※
大学的に…
例3の途中の運動方程式は、
\(ma=mg-ky\)
上式の両辺に\(v\)をかけて
\(\displaystyle{\scriptsize{\begin{eqnarray}&&mv a=mgv-ky・y\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=mg\frac{dy}{dt}-ky\frac{dy}{dt} \cdots①\\\\{\Leftrightarrow}&&\int_{t_{はじめ}}^{t_{あと}}{mv\frac{dv}{dt}}dt=\int_{t_{はじめ}}^{t_{あと}}{mg\frac{dy}{dt}}dt+\int_{t_{はじめ}}^{t_{あと}}{-ky\frac{dy}{dt}}dt\end{eqnarray}}}\)
ここで、\(t_{はじめ}→t_{あと}\)のとき、\(v_{はじめ}→v_{あと}\)、\(y_{A}→y_{B}\)とすると、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\int_{v_{はじめ}}^{v_{あと}}mvdv=\int_{y_A}^{y_B}mgdy+\int_{y_A}^{y_B}(-ky)dy\\\\{\Leftrightarrow}&&\left[\frac{1}{2}mv^2\right]_{v_{はじめ}}^{v_{あと}}=\left[mgy\right]_{y_A}^{y_B}+\left[\frac{1}{2}ky^2\right]_{y_A}^{y_B}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(y_B-y_A)-\frac{1}{2}k(y_B^2-y_A^2)\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(y_A^2-y_B^2)-mg(y_A-y_B)\end{eqnarray}}}\)
となり、例3でみた式と同じになります。
また、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left(\frac{1}{2}mv^2\right)&=&\frac{dv}{dt}・\frac{d}{dv}\left(\frac{1}{2}mv^2\right)\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\frac{dy}{dt}・\frac{d}{dy}(mgy)=mg\frac{dy}{dt}}\)
\(\displaystyle{\frac{dy}{dt}・\frac{d}{dy}\left(\frac{1}{2}ky^2\right)=ky\frac{dy}{dt}}\)
から、これらを①式に用いると、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}=mg\frac{dy}{dt}-ky\frac{dy}{dt}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left(\frac{1}{2}mv^2\right)=\frac{d}{dt}(mgy)-\frac{d}{dt}\left(\frac{1}{2}ky^2\right)\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2+\frac{1}{2}ky^2-mgy\right\}=0\end{eqnarray}}\)
上記の式は、{}内の式を時間\(t\)で微分すると\(0\)になるということを表しています。
すなわち、{}内の部分は定数であり、これは時間(t)を含まないので時間に依存しません。
なので、{}内は定数であり、どの時間においても一定の値なので
はじめ:
\(\displaystyle{\frac{1}{2}mv_{はじめ}^2+\frac{1}{2}ky_A^2-mgy_A=K}\)
あと:
\(\displaystyle{\frac{1}{2}mv_{あと}^2+\frac{1}{2}ky_B^2-mgy_B=K}\)
となり、上記2つの式の値は等しいので
\(\displaystyle{\scriptsize{\frac{1}{2}mv_{あと}^2+\frac{1}{2}ky_B^2-mgy_B=\frac{1}{2}mv_{はじめ}^2+\frac{1}{2}ky_A^2-mgy_A}}\)
が成り立つ、すなわち力学的エネルギー保存の法則が成り立ちます。
9.非保存力と力学的エネルギー
保存力である重力について、物体を初速度\(v_0\)で真上に投げた際、最高点\(h\)をあとの位置とすると、運動エネルギーと仕事の原理から
\(\displaystyle{\begin{eqnarray}&&\frac{1}{2}m・0^2-\frac{1}{2}mv_0^2=-mgh\\\\{\Leftrightarrow}&&\frac{1}{2}mv_0^2=mgh\end{eqnarray}}\)
となります。
物体は最高点に達してから一瞬静止しても、落下してもとの高さに戻るときには速さ\(v_0\)となります。
このことから、高さ\(h\)にある物体は、\(mgh\)の仕事をする能力をもっており、これを用いて運動エネルギーを生み出す能力をもっています。
しかし、非保存力である摩擦力については、一度止まってしまうと、自発的に動き出すことはなく運動エネルギーを生み出す能力をもっていません。
よって、はじめの運動エネルギーは回復されずに失われたままとなってしまいます(保存しない)。
一般的に、物体が保存力以外の力から仕事をされると、物体の力学的エネルギーはその分だけ変化し保存しません。
9.落下運動②
落下運動①では、直線上を運動する物体を扱いましたが、この記事では平面上を運動する物体を扱います。
運動する物体の扱いになるので、運動方程式を用いますが、今回は平面上を運動物体ですので\(x\)軸方向と\(y\)軸方向に関する運動方程式を立式します。
また、立式した運動方程式から\(v-t\)グラフを描きますが、こちらも\(x\)軸方向と\(y\)軸方向それぞれのグラフを描きます。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.落下運動について
落下運動①でみた自由落下や鉛直投げ上げなどは、1つの軸上(\(y\)軸上)での運動でした。
ここからは、\(x-y\)平面上での落下運動をみていくことにします。
(→落下運動①)
今回扱うのは、"水平投射"と"斜方投射"になります。
また、運動方程式を扱うので、こちらも参考にしてください。
→運動の3法則と束縛条件
2.水平投射
"水平投射"とは、物体を真横(水平方向)に投げた際の運動になります。
例を考えていきます。
質量\(m\)の物体を、ビルの上から右向きに初速度\(v_0\)で投げ出すことを考えます。
投げた物体は、右斜め下方向に運動するので、\(x\)軸を右向き正、\(y\)軸を下向き正として設定します。
原点は、物体が運動をはじめる直前(投げ出される直前)である、人の手を離れる瞬間を原点とします。
状況としては、下図のようになります。
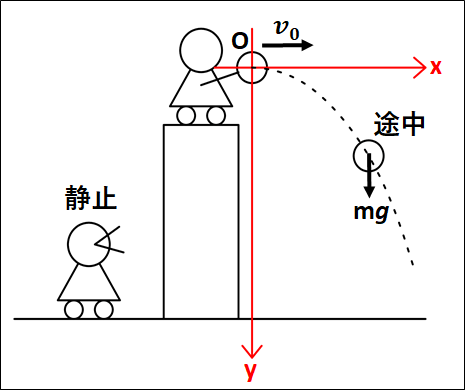
物体が運動している途中でかかっている力は、重力が鉛直下向きにはたらいています。
このことから、それぞれの軸方向にはたらいている力は、
\(x\)軸方向
→はたらいている力なし
\(y\)軸方向
→重力
となります。
重力は、\(y\)軸の正の方向にはたらいているので、\(+mg\)となります。
以上のことから、力の符合に注意して\(x\)軸方向と\(y\)軸方向に関して運動方程式を立てます。
\(x\)軸方向の加速度を\(a_x\)、\(y\)軸方向の加速度を\(a_y\)とすると、運動方程式は
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0 (x軸方向)\\ma_y=mg (y軸方向)\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{c}a_x=0 \textcolor{green}{(v_x-t{\bf{グラフの傾き}})}\\a_y=g \textcolor{green}{(v_y-t{\bf{グラフの傾き}})}\end{array}\right.\end{eqnarray}}\)
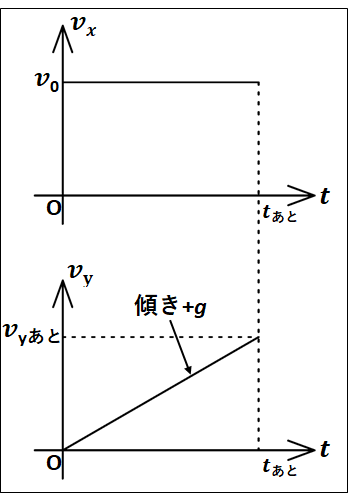
上式より、運動方程式が加速度について解けたので、\(x\)軸方向と\(y\)軸方向について\(v-t\)グラフを描いていきます。
その際、分かりやすいように縦に並べて描きます。
\(x\)軸方向のグラフを\(v_x-t\)グラフ、\(y\)軸方向のグラフを\(v_y-t\)グラフとします。
\(x\)軸方向の初速度を\(v_{xはじめ}\) とすると、はじめ\(x\)軸の正方向に\(v_0\)で投げたので、
\(v_{xはじめ} =v_0\)
また、運動方程式を解いた結果から
\(a_x=0\)
なので、グラフの傾きは\(0\)(\(x\)軸と平行)になります。
\(y\)軸方向の初速度を\(v_{yはじめ}\) とすると、はじめ\(y\)軸方向には速度を加えていません。
よって、
\(v_{yはじめ} =0\)
また、運動方程式を解いた結果から
\(a_y=g\)
なので、グラフの傾きは\(+g\)(右上がり)となります。
以上のことから、それぞれの\(v-t\)グラフを縦に並べて描くと下図のようになります。
\(v-t\)グラフは\(t_{あと}\)秒後までを描いています。
時間軸は、\(x\)方向の物体の運動と\(y\)軸方向の物体の運動とで共有しています。
ここからは覚える必要はありませんが…
○時刻\(t_{あと}\)における\(x\)軸方向の速度\(v_{xあと}\)
\(v_x-t\)グラフから、\(x\)軸方向の速度は常に一定の値\(v_0\)なので、
\(v_{xあと}=v_0\)
○時刻\(t_{あと}\)における\(y\)軸方向の速度\(v_{yあと}\)
\(v_y-t\)グラフにおける、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&g=\frac{v_{yあと}-0}{t_{あと}-0}\\\\\Leftrightarrow&&v_{yあと}=gt_{あと}\end{eqnarray}}\)
○時刻\(t_{あと}\)における\(x\)軸方向の物体の位置\(x\)
\(v_x-t\)グラフの面積から
\(\displaystyle{x=v_0t_{あと}}\)
○時刻\(t_{あと}\)における\(y\)軸方向の物体の位置\(y\)
\(v_y-t\)グラフの面積から
\(\displaystyle{\begin{eqnarray}y&=&\frac{1}{2}v_{yあと} t_{あと}\\\\&=&\frac{1}{2}gt_{あと}^2 (∵v_{yあと}=gt_{あと})\end{eqnarray}}\)
以上のように、様々なことを求めることができます。
また問題文中で、\(x\)軸か\(y\)軸のどちらかのみの情報しか与えられていない場合でも、\(v_x-t\)グラフと\(v_y-t\)グラフの時間軸は共有しているので、時間の値を介してもう片方の情報を求めることができます。
3.斜方投射
"斜方投射"とは、物体を斜め上に投げた際の運動になります。
こちらも例を考えていきます。
下図のように、水平方向と角度\(\theta\)をなす方向に、初速度\(v_0\)で投げ出した質量\(m\)の物体を考えます。
物体は投げ出されたあと、斜め右上方向に運動するので\(x\)軸の正を右方向、\(y\)軸の正を上方向にとります。
原点は、物体が投げ出される直前のところにとっています。
物体が運動している途中では、鉛直下向きに重力\(mg\)がかかっています。
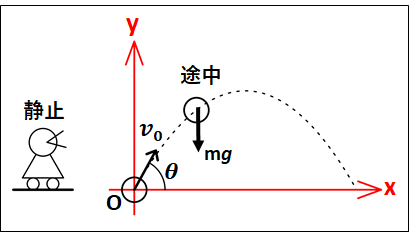
次に、\(x\)軸方向と\(y\)軸方向についての初速度を求めていきます。
物体は\(x\)軸と角度\(\theta\)をなす斜め方向に\(v_0\)で投げ出されているので、この初速度の\(x\)成分と\(y\)成分を考えます。
その際に直角三角形を考え、三角関数を用いて初速度\(v_0\)を\(x\)軸方向と\(y\)軸方向に分解します。
力(ベクトル)の分解にやベクトルの成分表示については、こちらを参考にしてください
→三角関数の定義と関係式
→力とベクトル
→練習問題1(三角関数の定義とグラフ)
→練習問題(ベクトル)
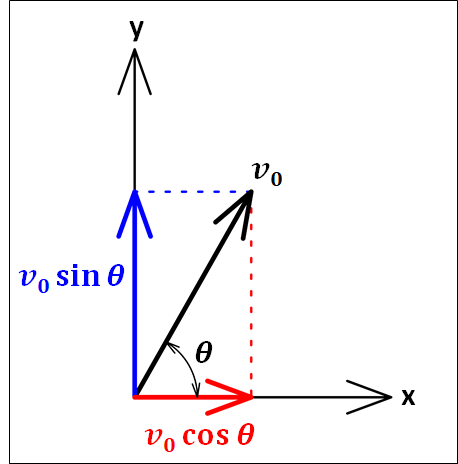
\(x\)軸方向と\(y\)軸方向の初速度を、それぞれ\(v_{xはじめ}\) 、\(v_{yはじめ}\) とします。
初速度を分解すると、\(x\)軸方向の成分に関しては\(\theta\)にへばりついている辺なので
\({\bf{斜辺}}×\cos\theta\)
となります。
実際に計算すると
\(v_{xはじめ} =v_0\cos\theta\)
また、\(y\)軸方向の成分に関しては、\(\theta\)の向かい側の辺になるので
\({\bf{斜辺}}×\sin\theta\)
となります。
実際に計算すると、
\(v_{yはじめ} =v_0\sin\theta\)
以上から、\(x\)軸方向と\(y\)軸方向の初速度が分かりました。
次は、物体は運動しているので運動方程式を立てます。
注意する点としては、物体にかかっている力は重力\(mg\)のみで、これは鉛直下向きにかかっています。
今、\(y\)軸は上向きを正としているので、重力は\(-mg\)となります。
これに注意して、水平投射のときと同様に\(x\)軸方向と\(y\)軸方向について運動方程式を立てると、
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0\\ma_y=-mg\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}a_x=0\\a_y=-g\end{array}\right.\end{eqnarray}}\)
運動方程式を加速度について解いたことで、それぞれの方向に関する\(v-t\)グラフの傾きが分かりました。
以上のことから、それぞれの\(v-t\)グラフを描くと、以下のようになります。
\(v-t\)グラフは、\(t_{あと}\)秒後までを描いています。
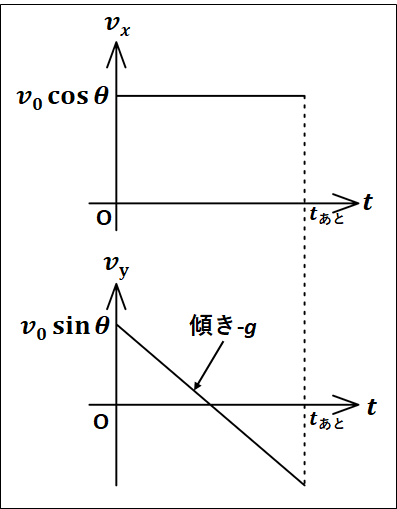
実際に問題を解く際には、この\(v-t\)グラフを用いて面積を求めたり、加速度の定義式を用いていくことになります。
8.運動の3法則と束縛条件
この記事では運動の3法則と束縛条件について解説しています。
特に、運動方程式に重点をおいています。
運動方程式の立て方や、利用の仕方を載せています。
また、空気抵抗についても解説しています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.運動の3法則
運動の3法則は以下の3つになります。
①慣性の法則(運動の第1法則)
②運動の法則(運動の第2法則)
③作用反作用の法則(運動の第3法則)
これらについて解説していきます。
\(\bf{\underline{①慣性の 法則(運動の第1法則)}}\)
物体は外から力を受けていないとき、あるいは受けていてもそれらがつりあっているとき、静止している物体は静止し続け、運動している物体は等速直線運動(速度が一定の運動)を続けます。
言い換えると、物体はその状態を維持しようとします。
※
質量が大きいほど、物体の状態は変わりにくい
質量についてはこちらも参考にしてください
→力のはたらきとつりあい
上記の性質を、\(\textcolor{red}{\bf{慣性の 法則}}\)といいます。
\(\bf{\underline{②運動の法則(運動の第2法則)}}\)
力を受けている物体は、その力の向きに加速度を生じます。
その加速度の大きさは、力の大きさに比例し、物体の質量に反比例します。
これを、\(\textcolor{red}{\bf{運動の法則}}\)といいます。
上記から、質量を\(m\)、物体の受けている力を\(F\)、生じる加速度を\(a\)、比例定数を\(k\)とすると以下のようになります。
\(\displaystyle{a=k\frac{F}{m}}\)

上式において、比例定数\(k\)が\(1\)となるように決められた力の単位が\(N\)(ニュートン)となります。
\(1N\)は、質量\(1kg\)の物体に\(1m/s^2\)の大きさの加速度を生じさせる力の大きさとなります。
上記が力の定義です。
運動の法則(運動の第2法則)を、質量\(m[kg]\)、加速度\(\vec{a}[m/s^2]\)、力\(\vec{F}[N]\)で表すと、
\(\displaystyle{\textcolor{red}{m\vec{a}=\vec{F}}}\)
上式を、\(\textcolor{red}{\bf{運動 方程式}}\)といいます。
"運動方程式"は、\(\textcolor{red}{\bf{動いている物体についての式}}\)になります。
また、"運動方程式"の右辺の\(\vec{F}\)は、物体にかかっている力の"合力"となります。
※
静止している物体
→つりあいの式を用いる
運動している物体
→運動方程式を用いる
加速度\(a\)は\(v-t\)グラフの傾きを表しているため、等速直線運動(速度が一定の運動)をしている物体については、\(a=0\)となります。(傾きが\(0\))。
また、物体にはたらいている力がつりあっているとき、合力が\(0\)なので運動方程式の右辺が\(0\)となります。
その結果、加速度\(a=0\)(\(v-t\)グラフの傾きが\(0\))となり、物体は等速直線運動をすることがわかります。
運動方程式は因果律を表しており、下図のような意味になります。

\(\bf{\underline{③作用反作用の法則(運動の第3法則)}}\)
2つの物体が、互いに力を及ぼしあうとき、作用と反作用は同一直線上にあり、逆向きで大きさが等しいです。
これを、\(\textcolor{red}{作用反作用の法則}\)といいます。
作用反作用の法則については、こちらで詳しく解説しています。
→力のはたらきとつりあい
2.運動方程式の利用
"運動方程式"は動いている物体に関する式になります。
動いている物体については、この運動方程式を立式し、\(v-t\)グラフを描いていきます。
この"運動方程式"の立て方について、解説していきます。
運動方程式の立て方は、以下のようになります。
①運動方程式を立てる物体について、かかっている力を図示する
②軸を設定する(\(x\)軸、\(y\)軸)
正の向きは、初速度が正となる方向または、物体が動く方向にとります。
(落下運動①で扱ったものと同じ)
③物体が受けている力を、設定した軸方向に分ける。
(力のベクトルを成分表示で考える)
※力の成分表示については、こちらも参考にしてください。
→力とベクトル
④それぞれの方向について、運動方程式を立てる
上記のことを、実際に例を用いてみていきます。
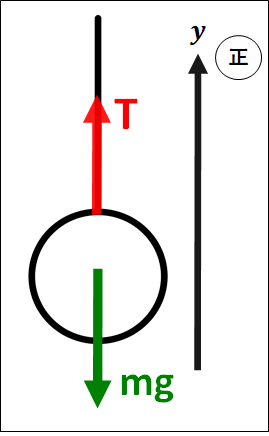
例)糸につながれて上昇している物体
(物体の質量を\(m\)、重力加速度を\(g\)とする)
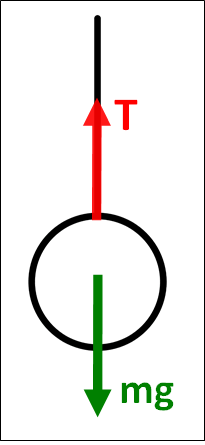
\(\bf{\underline{①かかっている力を図示する}}\)
まず、非接触力である"重力"が鉛直下向きにかかっています。
次に、物体の表面をなでまわすと糸とあたるので、この部分に張力\(T\)がかかっています。
向きは、糸が抜ける方向である鉛直上向きです。
\(\bf{\underline{②軸を設定する}}\)
物体は上昇しているので、鉛直上向きを正として\(y\)軸を設定します。
今回は、力が上下方向にしかかかっていないので\(y\)軸の設定だけします。
\(\bf{\underline{③力を軸方向に分ける}}\)
今回は、重力と張力のどちらも\(y\)軸に沿っているので、力を分ける必要はありません。
もしも、\(x\)軸や\(y\)軸に沿っていない力があれば、力を\(x\)軸や\(y\)軸方向にわけます。
これは、運動方程式を\(x\)軸方向や\(y\)軸方向について立式するためです。
(ベクトルそのものは扱いにくいので、\(x\)成分や\(y\)成分で考える)
\(\bf{\underline{④運動 方程式を立てる}}\)
図示した力と設定した軸から、張力\(T\)は正の向き、重力\(mg\)は負の向きになります。
このことから、\(y\)軸方向の加速度を\(a_y\)とすると、運動方程式は
\(\displaystyle{\begin{eqnarray}ma_y&=&(+T)+(-mg)\\\\&=&T-mg\end{eqnarray}}\)
となります。

※
今回は、左右方向(\(x\)軸方向)には力がはたらいていないので運動方程式を立てる必要は無いのですが、立てると以下のようになります。
\(x\)軸方向の加速度を\(a_x\)とします。
\(\displaystyle{ma_x=0}\)
今回左右方向には力がかかっていないので、その合力は\(0\)となります。
上式から、加速度\(a_x\)は\(0\)となり(両辺\(m\)で割った)、\(x\)軸方向の\(v-t\)グラフの傾きは\(0\)となります(\(x\)軸と平行になる)。
今回左右方向には動いていないので、はじめの速度は\(0\)なので、\(x\)軸方向の\(v-t\)グラフは、\(x\)軸と重なることになります。
上記のように運動方程式を立てた後は、加速度(\(v-t\)グラフの傾き)を求めるなどして、\(v-t\)グラフを描き、その結果から問題を解いていくことになります。
この運動方程式がわかると、落下運動①でしていたことが分かります。
→落下運動①
空中で物体にかかっている力は重力\(mg\)のみになります。
(空気抵抗は無視する)
この場合、鉛直上向きを正とした場合の\(y\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma_y=-mg\\\\\Leftrightarrow&&a_y=-g\end{eqnarray}}\)
となり、\(v-t\)グラフの傾きは\(-g\)となります。
これにより、グラフの傾きは右下がりになっていました。
鉛直下向きを正とした場合の\(y\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma_y=mg\\\\\Leftrightarrow&&a_y=g\end{eqnarray}}\)
となり、\(v-t\)グラフの傾きは\(g\)となります。
これにより、グラフの傾きは右上がりになっていました。
落下運動①で扱っていた、\(v-t\)グラフの傾きである重力加速度とその正負は、上記の運動方程式を立て、加速度について解いた結果を用いていました。
3.束縛条件
\(\textcolor{red}{\bf{束縛条件}}\)とは、"2つ以上の物体が連動して動くときの幾何学的条件"となります。
具体例をみてもらったほうが、わかりやすいと思います。
例1)
静止していた物体\(A\)と物体\(B\)が接した状態で、\(A\)に右向きに力を加えて動かしたとき。
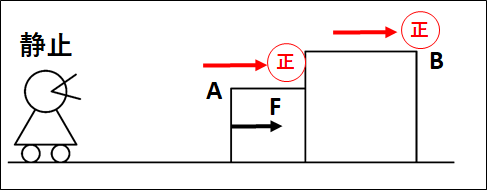
上図の状態では、\(A\)は力\(F\)を加えられて右向きに動きます。
\(B\)は、\(A\)に押されて右向きに動きます。
このとき、\(A\)と\(B\)の間にどのような関係があるかをみていきます。
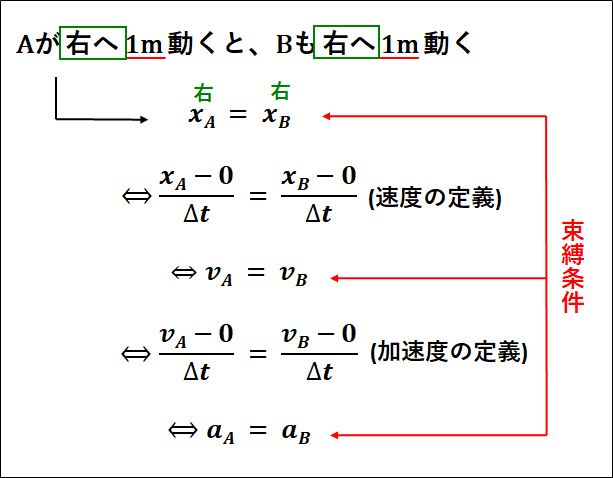
まず、\(A\)と\(B\)は接しているので、\(A\)が\(\textcolor{green}{\bf{右に}}\)\(\textcolor{red}{\bf{1m}}\)動くと、\(B\)も\(\textcolor{green}{\bf{右に}}\)\(\textcolor{red}{\bf{1m}}\)動きます。
このことから、\(A\)が動いた距離を\(x_A\)、\(B\)が動いた距離を\(x_B\)とすると、以下の式が成り立ちます。
\(x_A=x_B\)
また、速度の定義式を用いて、
(速度・加速度についてはこちら→変位・速度・加速度)
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}\frac{x_A-0}{\Delta{t}}&=&\frac{x_B-0}{\Delta{t}}\\\\{\Leftrightarrow}v_A&=&v_B\end{eqnarray}}\)
これより、\(A\)が右向きに動く速さと、\(B\)が右向きに動く速さが同じことがわかりました。
さらに、加速度の定義式を用いて、
\(\displaystyle{\begin{eqnarray}v_A&=&v_B\\\\{\Leftrightarrow}\frac{v_A-0}{\Delta{t}}&=&\frac{v_B-0}{\Delta{t}}\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
これより、\(A\)が右向きに生じる加速度の大きさと、\(B\)が右向きに生じる加速度の大きさが同じであることがわかりました。
以上のことから、束縛条件は
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}v_A&=&v_B\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
となります。
※
微分を用いて書くと、
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}\frac{dx_A}{dt}&=&\frac{dx_B}{dt}\\\\{\Leftrightarrow}v_A&=&v_B\\\\{\Leftrightarrow}\frac{dv_A}{dt}&=&\frac{dv_B}{dt}\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
となります。
例2)
滑車にかけられた糸の先端につながれている物体\(A\)、\(B\)について。
\(A\)が下向きに動いているとき。
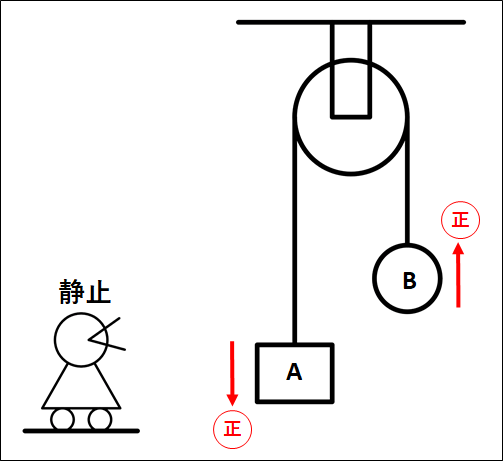
こちらについては、\(A\)と\(B\)は糸を介して繋がっており、糸は滑車にかけられているので、\(A\)が\(\textcolor{green}{\bf{下に}}\)\(\textcolor{red}{\bf{1m}}\)動くと、\(B\)は\(\textcolor{green}{\bf{上に}}\)\(\textcolor{red}{\bf{1m}}\)動きます。
それぞれの物体について、\(A\)を下向き正、\(B\)を上向きに正とします。
\(A\)が下向きに動いた距離を\(x_{A下}\)、\(B\)が上向きに動いた距離を\(x_{B上}\)とすると、動いた距離は同じになるので
\(\displaystyle{x_{A下}=x_{B上}}\)
となります。
動いた距離が同じなので、例1)のときと同様に、速度の定義と加速度の定義を用いていくと、
(\(x_{A下}=x_{B上}\)の両辺を\(t\)で微分していくと)
\(\displaystyle{\begin{eqnarray}x_{A下}&=&x_{B上}\\\\{\Leftrightarrow}v_{A下}&=&v_{B上}\\\\{\Leftrightarrow}a_{A下}&=&a_{B上}\end{eqnarray}}\)
となります。

これが、束縛条件となります。
例2)においては、それぞれの大きさは同じですが、向きが異なることに注意してください。
4.空気抵抗と終端速度
\(\bf{空気抵抗}\)は、空気中を運動する物体に対して、運動の向きとは"逆向き"にはたらく力になります。
速さが大きくない範囲では、空気抵抗の大きさは、速さに比例することが知られています。
よって、比例定数\(k\)を用いると空気抵抗の大きさは
\(\textcolor{green}{kv}\)
と表されます。
ここで、自由落下する質量\(m\)の物体を考えます。
落下する物体は、速度が大きくなっていきますが、速度が大きくなると空気抵抗も大きくなっていきます。
そのため、最終的に空気抵抗と重力がつりあい、速度は一定となります。
このときの速度\(v_f\)を\(\textcolor{red}{\bf{終端速度}}\)といいます。
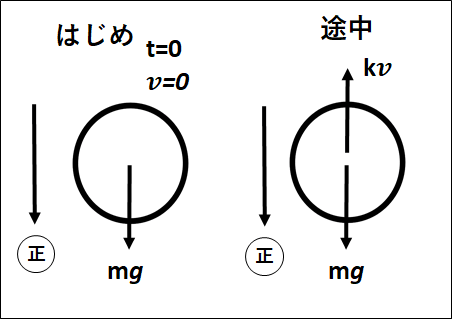
上図から、途中の運動方程式は
\(ma=mg-kv\cdots①\)
となります。
\(\bf{○はじめのとき}\)
はじめの状態では、\(v=0\)なので\(①\)に代入して
\(\displaystyle{\begin{eqnarray}ma&=&mg-k・0\\\\{\Leftrightarrow}ma&=&mg\\\\{\Leftrightarrow}a&=&g\end{eqnarray}}\)
よって、はじめの加速度は\(g\)となります。
\(\bf{○重力と空気抵抗がつりあったとき}\)
最終的には、重力と空気抵抗がつりあって速度は一定となるので\(a=0\)となります。(\(v-t\)グラフの傾きが\(0\))
このつりあったときの速度(終端速度)を\(v_f\)とすると、\(①\)から
\(\displaystyle{\begin{eqnarray}m・0&=&mg-kv_f\\\\{\Leftrightarrow}kv_f&=&mg\\\\{\Leftrightarrow}v_f&=&\frac{mg}{k}\end{eqnarray}}\)
これより、終端速度は
\(\displaystyle{v_f=\frac{mg}{k}}\)
となります。
\(v-t\)グラフは以下のようになります。
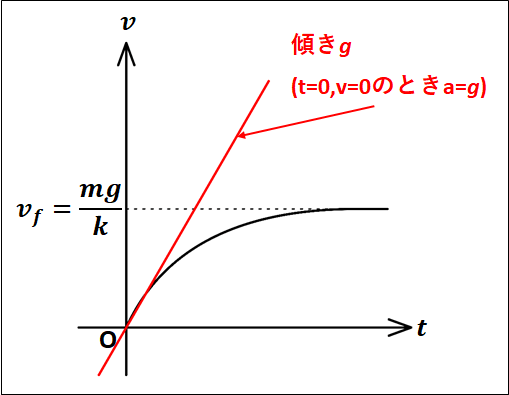
グラフ中に描いた傾き\(g\)は、\(t=0\)におけるグラフの接線になります。
また、グラフの各点における加速度は、その点における接線の傾きとなります。
グラフから、時間が経つにつれ速度が一定になっていく様子が分かると思います。
また、速さが小さいときの空気抵抗の大きさは\(kv\)と\(v\)に比例していましたが、速さが大きくなると\(kv^2\)と\(v^2\)に比例したものになります。
こちらも、終端速度を求めるだけならば、最終的に\(a=0\)となることを利用して、運動方程式から求めることができます。
\(\displaystyle{\begin{eqnarray}m・0&=&mg-k{v_f}^2\\\\{\Leftrightarrow}k{v_f}^2&=&mg\\\\{\Leftrightarrow}{v_f}^2&=&\frac{mg}{k}\end{eqnarray}}\)
から、
\(\displaystyle{v_f=\sqrt{\frac{mg}{k}}}\)
となります。
※
このグラフの関数を求めるには…
加速度の定義式から、
\(\displaystyle{a=\frac{dv}{dt}}\)
これより、途中の運動方程式は
\(\displaystyle{\begin{eqnarray}ma&=&mg-kv\\\\{\Leftrightarrow}m\frac{dv}{dt}&=&mg-kv\\\\{\Leftrightarrow}\frac{dv}{dt}&=&g-\frac{k}{m}v\end{eqnarray}}\)
となります。
上式は、「1階線形微分方程式」と呼ばれるもので、これを解くことで\(v\)と\(t\)の関係式を導くことができます。
興味があれば、調べてみてください。
