13.単振動
この記事では単振動を扱っています。
単振動は、等速円運動の正射影となります。
単振動に関する運動方程式の解き方や、一般解、単振動のエネルギーについても解説しています。
また、水平ばね振り子や鉛直ばね振り子の紹介もしています。
鉛直ばね振り子では、つりあいの位置を原点にしたものと、自然長の位置を原点にしたものの2通りをみています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
→単振動
Twitterアカウント→@roke_blog
目次
1.単振動とは
\(\textcolor{red}{\bf{単振動}}\)とは、
①等速円運動の正射影と同じ運動であり
②運動方程式が
\(ma=-k(x-x_0)\)
の形
のものとなります。
上記の①、②についてみていきます。
円運動についてはこちら
→円運動と慣性力
\(\underline{\bf{①等速円運動の正射影}}\)
次のように、半径(A)の円周上を①→②→③→④→①と移動する物体を考えます。
この物体をある一方向からみたものが正射影となります。
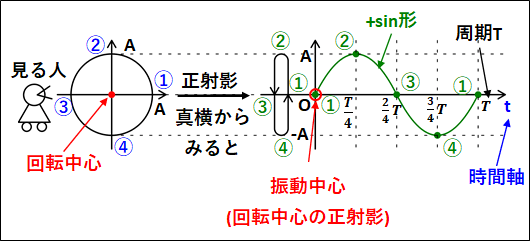
真横からみているので、奥行き方向(図中での左右方向)の動きは分からず、上下方向の動きのみをみています。
この上下方向の動きと、時間の関係を表したグラフが図中右側のグラフとなっています。
これは、三角関数のグラフと同じ形になっています。
※三角関数のグラフについてはこちら
→三角関数のグラフ
また、上記では真横からみましたが、真上からみると次のようになります。
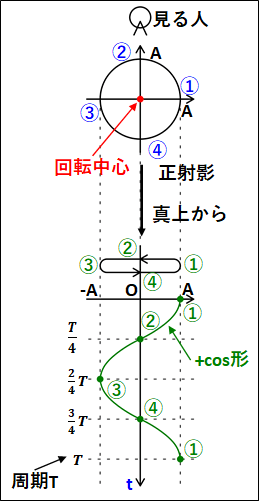
こちらに関しても真上から見ているので、みている人からは図中の上下方向の動きはわからず、左右方向の動きしかわかりません。
左右方向の動きと、時間の関係を表したグラフが図中の下のグラフになります。
上記の円の半径\(A[m]\)を\(\textcolor{red}{\bf{振幅}}\)といいます。
振幅は、振動中心からの変位の最大値となります。
(振動中心から最も離れたとき、中心からの距離が\(A[m]\)となる)
また、単振動は等速円運動の正射影と同じ運動であるといいましたが、用いる量もだいたいおなじとなります。
ただし、名称が多少変わっているものもあります。
・角振動数:\(\omega[rad/s]\)
(等速円運動では、角速度と呼んでいた)
こちらも、扱いは変わらず単位時間あたりに進む角度を表しています。
\(t\)秒間で進む角度は等速円運動のときと同様に\(\omega{t}[rad]\)となります。
・位相:\(\omega{t}[rad]\)
こちらは、等速円運動においては時刻\(t\)のときの回転角を表していました。
単振動では、時刻\(t\)における物体の状態を表します。
・周期:\(T[s]\)
単振動における周期\(T[s]\)は、物体が一回往復する時間となります。
(等速円運動とおなじく、\(T[s/(回)]\)と考えると良い)
また、こちらも等速円運動における回転数と同様に、逆数は1秒間に何回振動するかを表し、これを"振動数\(f[Hz]\)"といいます。
(\(Hz=/s , f[(回)/s]\)と考えるとよい)
\(\displaystyle{f[Hz]=\frac{1}{T[s]}}\)
\(\displaystyle{\left(f[(回)/s]=\frac{1}{T[s/(回)]}\right)}\)
また、
\(\displaystyle{\begin{eqnarray}&&T=\frac{2\pi}{\omega}\\\\{\Leftrightarrow}&&\omega=\frac{2\pi}{T}\end{eqnarray}}\)
となります。
上記の周期と振動数の関係を用いると
\(\displaystyle{\omega=\frac{2\pi}{T}=2{\pi}f}\)
と表すこともできます。
※周期について
後ほど詳しく説明しますが…
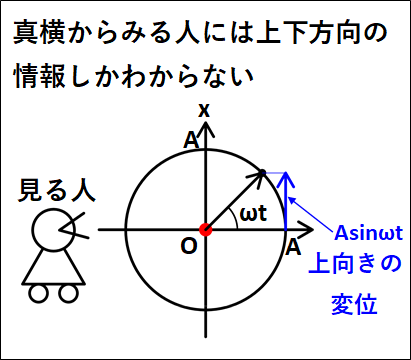
上記の真横からみた正射影について、回転する円を次のように設定します。
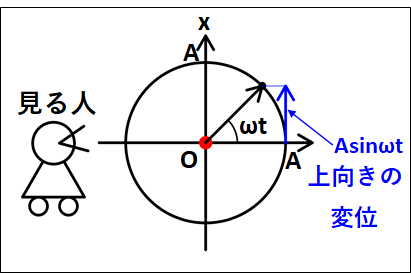
上向きの軸を\(x\)としたので、これは\(x\)軸への投射となります。
真横からみている人には、図中の左右方向の情報はわからないので、上下方向の情報のみがわかることになります。
よって、上下方向の変位のみを考えると、現在角度\(\omega{t}\)、半径\(A\)なので三角関数から上向きのベクトルは
\(+A\sin\omega{t}\)
となります。
これが、正射影されたグラフの\(x\)座標となるので、\(x=A\sin\omega{t}\)となります。
ここで、周期について考えてみます。
"1周まわる時間=周期\(T[s]\)"
なので、\(\displaystyle{\frac{1}{4}}\)回転なら\(\displaystyle{\frac{T}{4}[s]}\)となります。
よって、正射影のグラフで区間ごとに区切って載せていたのは、\(\displaystyle{\frac{1}{4}}\)回転ごとの区間となります。
また、先ほどみたように真横から見た振動の式は
\(x=A\sin\omega{t} \cdots①\)
先ほど説明したように、\(A\)を"振幅"といいます。
\(①\)式を変形すると
\(\displaystyle{\begin{eqnarray}x&=&A\sin\omega{t}\\\\&=&\sin\frac{2\pi}{\textcolor{blue}{\frac{2\pi}{\omega}}}t\end{eqnarray}}\)
となり、\(2\pi{t}\)の分母が周期となるので、
\(\displaystyle{x=\sin2\pi\frac{t}{\textcolor{blue}{T}}}\)
となり、周期は
\(\displaystyle{T=\frac{2\pi}{\omega}}\)
となることがわかります。
周期については、こちらも参考にしてください
→三角関数の定義と関係式
→三角関数のグラフ
\(\underline{\bf{②単振動と運動 方程式}}\)
単振動とは、運動方程式が
\(ma=-k(x-x_0)\)
の形になるものをいいます。
上式の形において、
"Kは正の値で"
"\(x_0\)は振動中心"
"\(-k(x-x_0)\)の部分を復元力"
と呼びます。

また、等速円運動の正射影や周期に関する話でみたように、真横からみて\(x\)軸へ投射された単振動の式は
\(\textcolor{red}{x=A\sin\omega{t}}\)
と表せます。
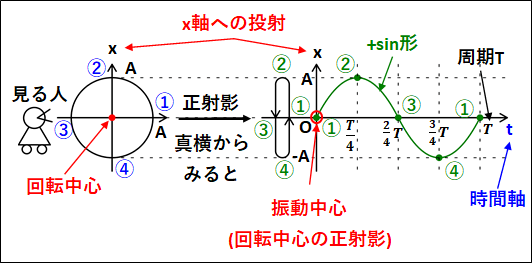
これを、時間\(t\)で微分したものが、速度\(v\)となります。
微分については、円運動で扱ったものとおなじようにします。
→円運動と慣性力
→微分法とその応用
実際に微分すると
\(\displaystyle{\textcolor{red}{v=\frac{dx}{dt}=A\omega\cos\omega{t}}}\)
さらに時間\(t\)で微分すると加速度となります。
\(\displaystyle{\textcolor{blue}{a=\frac{dv}{dt}=-A{\omega}^2\sin\omega{t}}}\)
ここで、\(\textcolor{green}{x=A\sin\omega{t}}\)なので、
\(\displaystyle{\begin{eqnarray}a&=&-{\omega}^2\textcolor{green}{A\sin\omega{t}}\\\\{\Leftrightarrow}a&=&-{\omega}^2\textcolor{green}{x}\end{eqnarray}}\)
となります。

上記では微分を用いて、変位の式から速度と加速度の式を導きましたが、速度、加速度を真横から見る人から考えることもできます。
等速円運動の部分で扱ったように、速度は大きさ\(r\omega\)で接線方向になります。
真横から見るひとには、この速度の上下方向の情報しかわからないので、下図のようになります。
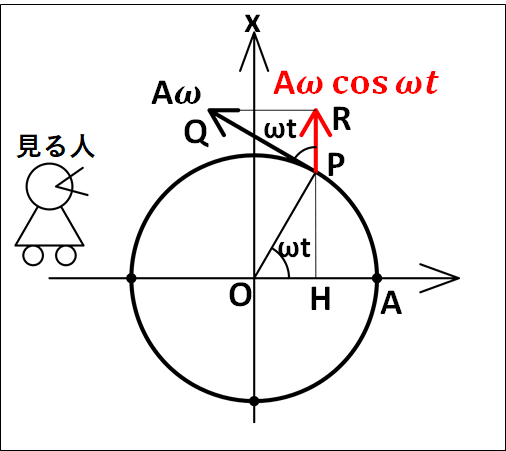
図中の赤いベクトルである\(\textcolor{red}{A\omega\cos\omega{t}}\)が、真横の人がみる速度ベクトル、すなわち単振動における速度となります。
※
図中に記した点\(O,H,P,Q,R\)について
\(Q\)
→円運動における速度ベクトルの終点
\(P\)
→円運動する物体の時刻\(t\)における位置
\(R\)
→円運動における速度ベクトルの上下方向成分の終点
\(\angle{PHO}=90°\)なので、\(\angle{OPH}=90°-\omega{t}\)
また、\(PQ\)は点Pにおける円の接線なので
\(\angle{OPQ}=90°\)
また、
\(\angle{OPH}+\angle{OPQ}+\angle{QPR}=180°\)
以上から、
\(\displaystyle{\begin{eqnarray}&&\angle{OPH}+\angle{OPQ}+\angle{QPR}=180°\\\\{\Leftrightarrow}&&(90°-\omega{t})+90°+\angle{QPR}=180°\\\\{\Leftrightarrow}&&\angle{QPR}=\omega{t}\end{eqnarray}}\)
となります。
これと、三角関数から円運動における速度の上下方向成分は
\(\displaystyle{\begin{eqnarray}\overrightarrow{PR}&=&|\overrightarrow{PQ}|\cos\omega{t}\\\\&=&A\omega\cos\omega{t}\end{eqnarray}}\)
となります。
加速度については、下図のように考えます。
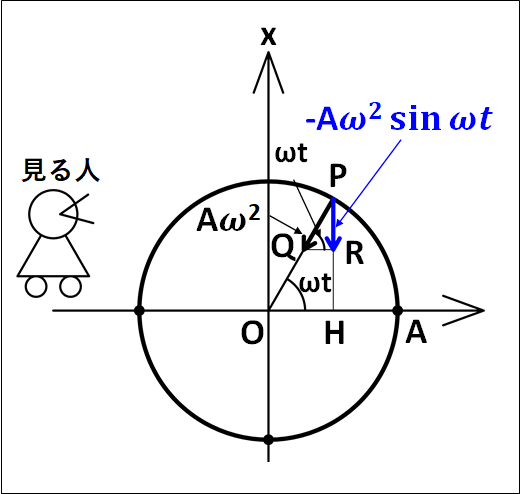
図中の青いベクトルである\(\textcolor{blue}{-A{\omega}^2\sin\omega{t}}\)が、真横の人がみる加速度ベクトル、すなわち単振動における加速度となります。
※
図中に記した点\(O,H,P,Q,R\)について
\(Q\)
→円運動における加速度ベクトルの終点
\(P\)
→円運動する物体の時刻(t)における位置
\(R\)
→円運動における加速度ベクトルの上下方向成分の終点
\(\overrightarrow{PQ}\)を上下左右方向に分解した上下方向のベクトルが\(\overrightarrow{PR}\)となります。
\(PR\)と\(Q R\)は直角なので、
\(Q R//OH\)
となります。
また、斜辺である\(OP\)は共通なので
\(\angle{POH}=\angle{PQR}=\omega{t}\)
これと、三角関数から円運動における加速度の上下方向成分は
\(\displaystyle{\begin{eqnarray}\overrightarrow{PR}=-|\overrightarrow{PQ}|\sin\omega{t}\\\\=-A{\omega}^2\sin\omega{t}\end{eqnarray}}\)
となります。
(いま上向き正で、速度の上下方向の成分は下向きなのでマイナスがつく)
以上のことから分かることは、
①運動方程式を変形して、
\(a=-□(x-x_0)\)
の\(□\)は\({\omega}^2\)を表す。
②
\(\displaystyle{a=-{\omega}^2x {\Leftrightarrow} ma=\textcolor{blue}{-m{\omega}^2x}}\)
上式の\(\textcolor{blue}{-m{\omega}^2x}\)部分を\(\textcolor{blue}{\bf{復元力}}\)と呼ぶ
2.単振動の運動方程式の解き方
\(\displaystyle{\begin{eqnarray}ma=-k(x-x_0)\\\\{\Leftrightarrow}a=-\textcolor{red}{\frac{k}{m}}(x-x_0)\end{eqnarray}}\)
上式の変位\(x\)の係数である\(\displaystyle{\textcolor{red}{\frac{k}{m}}}\)が、角振動数\(\omega\)の情報を与えます。
(\(a=-{\omega}^2x\)から)
これより、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
となります。
(高校物理においては、角振動数は正として扱ってよい)
このとき、
\(\displaystyle{a=-\frac{k}{m}(\textcolor{green}{x-x_0})}\)
の\( (\textcolor{green}{x-x_0})\)をそのまま左辺にもってきて
\(\displaystyle{\textcolor{green}{x-x_0}=±A\cos\left(\sqrt{\frac{k}{m}}t\right)}\)
または
\(\displaystyle{\textcolor{green}{x-x_0}=±B\sin\left(\sqrt{\frac{k}{m}}t\right)}\)
となります。
上式の\(±\sin\)や\(±\cos\)のうちのどの形をとるかは、問題で判断します。

3.単振動の一般解
単振動の一般解には、三角関数の合成式
\(\displaystyle{A\cos\theta+B\sin\theta=\sqrt{A^2+B^2}\sin(\theta+\alpha)}\)
を用います。
合成式についてはこちら
→三角関数の公式
\(\theta\)を\(\omega{t}\)とすると、
\(\displaystyle{A\cos\omega{t}+B\sin\omega{t}=\sqrt{A^2+B^2}\sin(\omega{t}+\alpha)}\)
となります。
ここで、
\(\displaystyle{\sqrt{A^2+B^2}}\)で振幅が
\(\displaystyle{\omega}\)は\(\displaystyle{\omega=\frac{2\pi}{T}}\)によって周期が
\(\alpha\)によって、\(t\)軸方向にどれだけ平行移動しているか
がそれぞれ決まるので、
\(\displaystyle{\sqrt{A^2+B^2}\sin(\omega{t}+\alpha)}\)
はどのような波の式(単振動の式)も表すことができます。
すなわち、
\(\displaystyle{A\cos\omega{t}+B\sin\omega{t}}\)
もどのような波(単振動)の式も表すことができます。
これによって、
\(\displaystyle{x-x_0=A\cos\omega{t}+B\sin\omega{t}}\)
において、定数\(A , B\)が決まれば、単振動による物体の位置が表せることになります。
また、位置の式
\(\displaystyle{x-x_0=A\cos\omega{t}+B\sin\omega{t}}\)
を時間\(t\)で微分すると速度\(v\)が、速度\(v\)の式を時間\(t\)で微分すると加速度\(a\)が求まります。
これらを用いて、初期条件(\(t=0\)のときの条件)から定数\(A , B\)を定めることで、物体の位置・速度・加速度の情報を得ることができます。
したがって、単振動する物体の位置を表す式の一般解は次のようになります。
\(\textcolor{green}{\underline{\bf{単振動する物体の位置を表す一般解}}}\)
\(\displaystyle{\textcolor{green}{x-x_0=A\cos\omega{t}+B\sin\omega{t}}}\)
4.運動方程式解き方練習
例)
図のようにばねにつながれた質量\(m\)の物体を、自然長から\(A\)だけ伸ばした状態で静かに放すことを考える。
(ばね定数は\(k\)、床はなめらかとする)
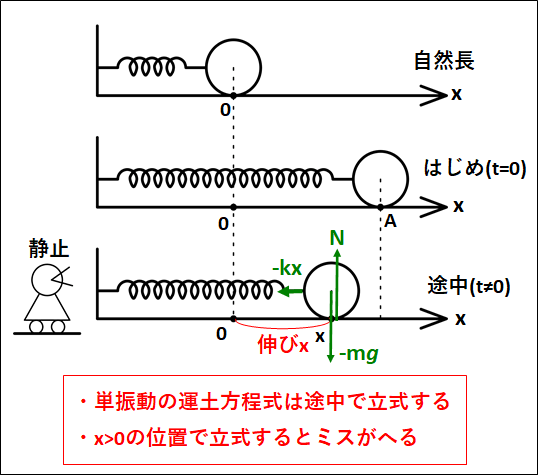
途中での\(x\)方向に関する運動方程式は、
(途中での物体の位置を\(x\)とする)
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\\\\{\Leftrightarrow}&&a=-\frac{k}{m}(x-0)\end{eqnarray}}\)
※よくあるミス
\(× ma=-kA\)
\(× ma=kx\)
よって、
\(\displaystyle{{\omega}^2=\frac{k}{m}}\)
から、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
振動中心は\(x=0\)
※
\(\displaystyle{\textcolor{red}{a=-\frac{k}{m}(x-x_0)}}\)
において、振動中心は\(x_0\)
今回は、\(x_0=0\)なので、振動中心は\(x=0\)の位置となる
物体は、はじめ\(A\)の位置にいて、そこから負の方向へ動き出し、\(x=0\)を振動中心として振動する。
よって、下図のように\(①→②→③→④→①\)のように動きます。
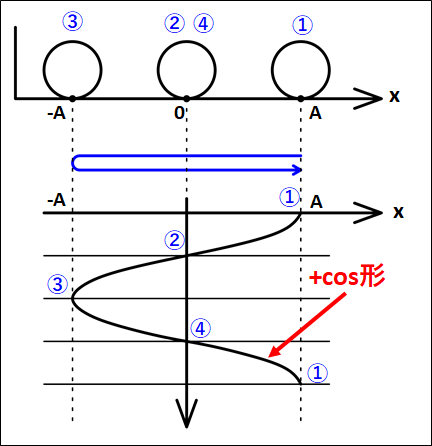
グラフの形は、はじめ正の位置にいて、そこから\(0\)→負→\(0\)→正のように動いていきます。
なので、これは\(\textcolor{red}{+\cos}\)形となります。
また振幅は、振動中心からの最も離れるときの距離なので
\(\textcolor{red}{\bf{振幅=|最初の位置-振動中心|}}\)
となり、今回は
\(\displaystyle{\begin{eqnarray}{\bf{振幅}}&=&{\bf{|最初の位置-振動中心|}}\\\\&=&|A-0|\\\\&=&A\end{eqnarray}}\)
となります。
以上から、物体の変位の式は運動方程式の解き方で解説したように、\(x-0\)をそのままもってきて
\(\displaystyle{\begin{eqnarray}x-0&=&A\cos\omega{t}\\\\&=&A\cos\sqrt{\frac{k}{m}}t\\\\&=&A\cos2\pi\frac{t}{\textcolor{green}{2\pi\sqrt{\frac{m}{k}}}}\end{eqnarray}}\)
上式における\(2\pi{t}\)の分母が周期となるので、周期\(T\)は
\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}}\)
変位の式は
\(\displaystyle{x=A\cos\sqrt{\frac{k}{m}}t}\)
速度の式を求めるために、変位の式を時間\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
これは、\(-\sin\)形となります。
さらに、加速度の式を求めるために、速度の式を時間\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A\frac{k}{m}\cos\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
これは、\(-\cos\)形となります。
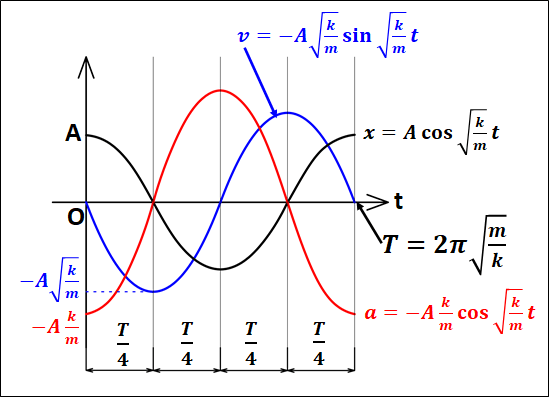
次に求めた変位・速度・加速度の関係をグラフで表すと、下図のようになります。
(変位・速度・加速度それぞれの最大値の大小関係は適当)
\(\underline{\bf{※一般解を用いると}}\)
運動方程式を立てて、振動中心\(x=0\)および、角振動数\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)までは求めているとします。
単振動の変位の式の一般解から、
(例題で最初の伸びに\(A\)が使われているので、一般解において\(A\)を\(A'\)とした)
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t} \cdots①}\)
\(t\)で微分して
\(\displaystyle{v=-A'\omega\sin\omega{t}+B'\omega\cos\omega{t} \cdots②}\)
さらに\(t\)で微分して
\(\displaystyle{a=-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t} \cdots③}\)
初期条件(\(t=0\)のときの条件)は、
\(t=0\)のとき、\(x=A\)、\(v=0\)
なので、これらを\(①、②\)に代入すると、
\(①\)から
\(\displaystyle{\begin{eqnarray}&&A=A'\cos0+B'\sin0\\\\{\Leftrightarrow}&&A=A'\end{eqnarray}}\)
(\(\cos0=1 , \sin0=0\))
\(②\)から
\(\displaystyle{\begin{eqnarray}&&0=-A'\omega\sin0+B'\omega\cos0\\\\{\Leftrightarrow}&&B'=0\end{eqnarray}}\)
以上から、\(A'=A , B'=0\)を\(①,②,③\)にそれぞれ代入すると
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\sqrt{\frac{k}{m}}t\end{eqnarray}}\)
\(\displaystyle{ \begin{eqnarray} v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\sqrt{\frac{k}{m}}t \end{eqnarray} }\)
\(\displaystyle{ \begin{eqnarray} a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\sqrt{\frac{k}{m}}t \end{eqnarray} }\)
と、先ほどみた式と同じ式がでてきます。
5.水平ばね振り子
先ほどみた例と同じとなりますが…
なめらかな水平面上に、一端を固定したばね(ばね定数\(k\))の多端に質量\(m\)のおもりをつなぎます。
下図のような状態で、ばねを\(A\)だけ引き伸ばし、静かに手を離したときのおもりの運動をみてみます。
(自然長の位置を原点とする)
上記の、"ばねを\(A\)だけ引き伸ばし、静かに手を離す"という部分が初期条件(\(t=0\)のときの条件)となります。
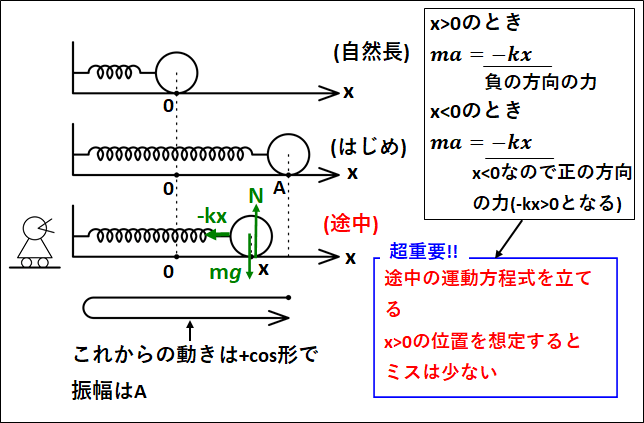
\(x\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\\\\{\Leftrightarrow}&&a=-\frac{k}{m}(\textcolor{green}{x}-\textcolor{red}{0})\end{eqnarray}}\)
よって、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
また、\((\textcolor{green}{x}-\textcolor{red}{0})\)から、
振動中心は原点で、振幅は
\(|A-0|=A\)
であることがわかります。
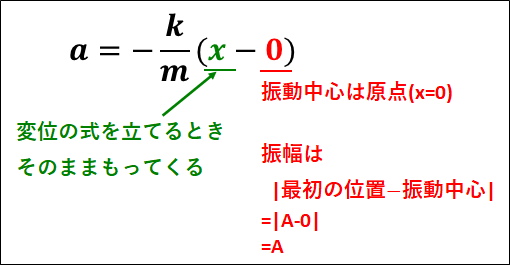
以上から、グラフが\(+\cos\)形であることに注意して、変形した運動方程式の\(\textcolor{green}{x}\)をそのまま左辺にもってきて、変位の式を立てると
\(\displaystyle{\begin{eqnarray}\textcolor{green}{x}&=&\textcolor{red}{A\cos}\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
上式の、
\(\displaystyle{\textcolor{red}{+A\cos}}\)
は問題から読み取る情報となります。
また、\(2\pi{t}\)の分母が周期\(T\)となることから
\(\displaystyle{\textcolor{blue}{T=2\pi\sqrt{\frac{m}{k}}}}\)
となります。
上記変位の式を\(t\)で微分して、
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(2\pi\frac{t}{2\pi\sqrt{\frac{m}{k}}}\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\frac{k}{m}\cos\left(2\pi\frac{t}{2\pi\sqrt{\frac{m}{k}}}\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。
(例で扱ったものとおなじ)

一般解を用いても同様にして
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t}}\)
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}\end{eqnarray}}\)
初期条件\(t=0\)のとき、\(x=A , v=0\)を上式に代入して
\(A'=A , B'=0\)
と決まります。
6.鉛直ばね振り子
ばね定数\(k\)のばねを天井からつるし、他端に質量\(m\)のおもりを静かにつるすと、伸びが\(x_0\)になって静止したとする。
静止した位置からおもりをさらに\(A\)だけ引いて静かに離すことを考える。
(軸は鉛直下向き)
状況を図示すると、下図のようになります。
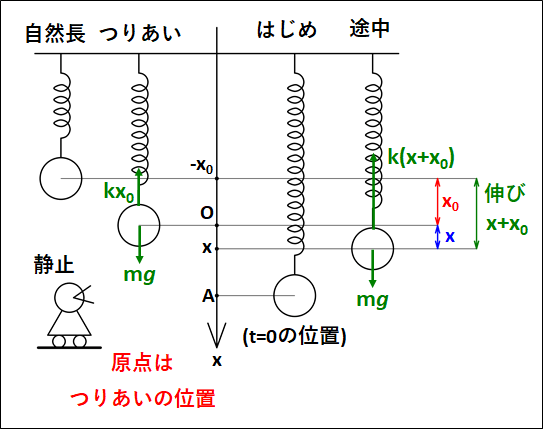
"\(\textcolor{red}{\bf{つりあいの位置}}\)を原点"としています。
まず、つりあっているときに関してですが、上下方向のつりあいより
\(kx_0=mg\)
次に途中の物体の位置を\(x\)とすると運動方程式は、
\(\displaystyle{\begin{eqnarray}&&ma=mg-k(x+x_0)\\\\{\Leftrightarrow}&&ma=mg-kx-kx_0\end{eqnarray}}\)
途中での自然長からの伸びは\(x\)ではなく、\(x+x_0\)であることに注意してください。
また、つりあいの式 \(kx_0=mg\) から、
\(\displaystyle{\begin{eqnarray}&&ma=mg-kx-kx_0\\\\{\Leftrightarrow}&&ma=\textcolor{red}{\cancel{\textcolor{black}{mg}}}-kx-\textcolor{red}{\cancel{\textcolor{black}{mg}}}\\\\{\Leftrightarrow}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\end{eqnarray}}\)
より、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
となります。
また、つりあいの位置を原点にしたことで、運動方程式がきれいな形になっていることを確認してください。
振動の形は、\(t=0\)で\(x=A\gt0\)。
そこから、\(x\)の負の方向へと運動するので\(+\cos\)形となります。
(\(+\cos\)のグラフも正→0→負→0→正と変化していく)
また、振動中心は\(x=0\)、振幅は
\(|A-0|=A\)
よって、変位の式は
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
周期\(T\)は、\(2\pi{t}\)の分母なので
\(\displaystyle{\textcolor{blue}{T=2\pi\sqrt{\frac{m}{k}}}}\)
変位の式を、\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\&=&-A\frac{k}{m}\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。

一般解を用いると、
初期条件\(t=0\)で\(x=A , v=0\)から定数\(A , B\)が決まります。
初期条件と角振動数が同じなので、水平ばね振り子と同じ式になります。
\(\underline{\bf{<類題>}}\)
先ほどの鉛直ばね振り子において、自然長を原点とするとどうなるのか?
状況は下図のようになります。
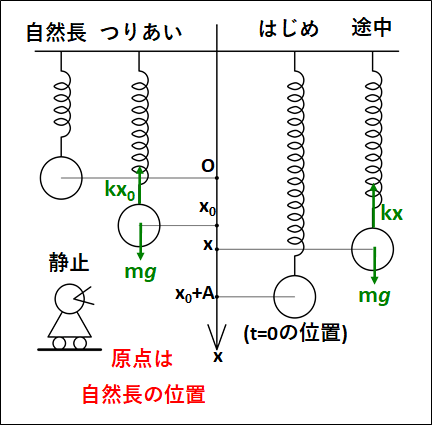
つりあい位置での上下方向のつりあいより
\(kx_0=mg\)
はじめの位置は、つりあいの位置からさらに\(A\)だけ下げたところになるので、座標は\(x_0+A\)になることに注意してください。
また、今回は自然長の位置を原点にしているので、途中の位置\(x\)におけるばねの自然長からの伸びは\(x\)となり、弾性力は上向きに\(kx\)となります。
よって、途中の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&ma=mg-kx\\\\{\Leftrightarrow}&&ma=-k\left(x-\frac{mg}{k}\right)\\\\{\Leftrightarrow}&&a=-\frac{k}{m}\left(x-\textcolor{red}{\frac{mg}{k}}\right)\end{eqnarray}}\)
これより、角振動数は
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
振動中心は
\(\displaystyle{x=\frac{mg}{k}=x_0}\)
となります。
(つりあいの式\(kx_0=mg\)を式変形すると、\(\frac{mg}{k}=x_0\)となる)
振幅は、|はじめの位置-振動中心| から、
\(\displaystyle{\begin{eqnarray}|x_0+A-\frac{mg}{k}|&=&|x_0+A-x_0| (∵\frac{mg}{k}=x_0)\\\\&=&A\end{eqnarray}}\)
よって、この物体の運動は\(x=x_0=\frac{mg}{k}\)を振動中心として振幅\(A\)で振動することが分かります。
また、振動の形はつりあいの位置を原点にとったときと同様に\(+\cos\)形です。
よって、変位の式は
\(\displaystyle{x-\frac{mg}{k}}\)
をそのまま左辺にもってきて
\(\displaystyle{\begin{eqnarray}&&x-\frac{mg}{k}=A\cos\omega{t}\\\\{\Leftrightarrow}&&x-\frac{mg}{k}=A\cos\left(\sqrt{\frac{k}{m}}t\right)\\\\{\Leftrightarrow}&&x=A\cos\left(\sqrt{\frac{k}{m}}t\right)+\frac{mg}{k}\\\\{\Leftrightarrow}&&x=A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{m}{k}}}}\right)+\frac{mg}{k}\end{eqnarray}}\)
上式は、\(x=A\cos\left(\sqrt{\frac{k}{m}}t\right)\)のグラフを、\(x\)軸方向に\(+\frac{mg}{k}\)平行移動したものとなります。
三角関数のグラフの平行移動についてはこちら
→三角関数のグラフ
またこれまでと同様に、\(2\pi{t}\)の分母が周期なので、
\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}}\)
求めた変位の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}t\right)\end{eqnarray}}\)
速度の式をさらに\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}t\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは下図のようになります。
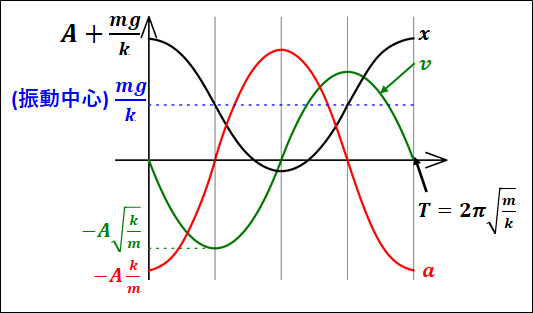
一般解を用いると、
\(\displaystyle{a=-\frac{k}{m}(x-\frac{mg}{k})}\)
から、
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
また、振動中心
\(\displaystyle{x=\frac{mg}{k}}\)
よって、
\(\displaystyle{x-\frac{mg}{k}=A'\cos\omega{t}+B'\sin\omega{t}}\)
変位の一般解の式を\(t\)で微分して
\(\displaystyle{v=-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}}\)
速度の式を\(t\)で微分して
\(\displaystyle{a=-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}}\)
初期条件\(t=0\)で\(x=x_0+A\)、\(v=0\)なので、まず変位の式に代入して
\(\displaystyle{\begin{eqnarray}x_0+A-\frac{mg}{k}=A'\cos0+B'\sin0\end{eqnarray}}\)
\(\displaystyle{x_0=\frac{mg}{k}}\)なので、
\(\displaystyle{\begin{eqnarray}&&x_0+A-\frac{mg}{k}=A'\cos0+B'\sin0\\\\{\Leftrightarrow}&&\frac{mg}{k}+A-\frac{mg}{k}=A'×1+B'×0\\\\{\Leftrightarrow}&&A'=A\end{eqnarray}}\)
次に、速度の式に代入して
\(\displaystyle{\begin{eqnarray}&&0=-A'\omega\sin0+B'\omega\cos0\\\\{\Leftrightarrow}&&B'=0\end{eqnarray}}\)
\(A'=A , B'=0\)をそれぞれの式に戻すと、
\(\displaystyle{\begin{eqnarray}&&x-\frac{mg}{k}=A\cos\omega{t}\\\\{\Leftrightarrow}&&x=A\cos\left(\sqrt{\frac{k}{m}}t\right)+\frac{mg}{k}\end{eqnarray}}\)
\(\displaystyle{v=-A\sqrt{\frac{k}{m}}\sin\left(\sqrt{\frac{k}{m}}\right)}\)
\(\displaystyle{a=-A\frac{k}{m}\cos\left(\sqrt{\frac{k}{m}}\right)}\)
と、先ほどみた式と同じものになります。
7.単振り子
糸の上端を固定して、下端におもりをつけ、おもりを\(\textcolor{red}{\bf{わずか}}\)に引いて静かに手を離す。
(糸の長さを\(l\)、おもりを\(A\)だけ引くとする)
下図のようにはじめと途中、また糸が鉛直になるときを考えます。
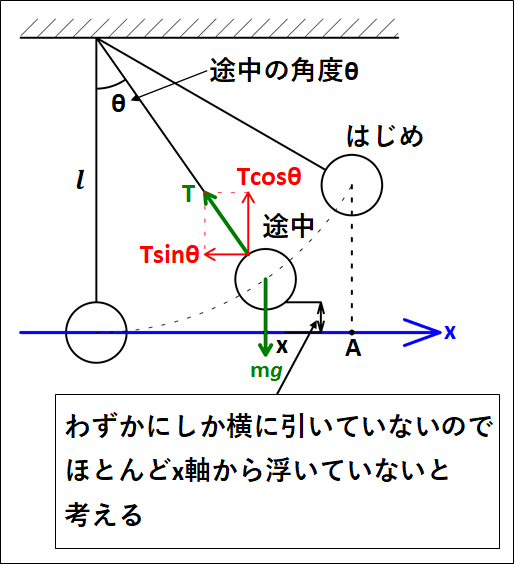
途中の\(x\)座標を\(x\)、そのときの鉛直な方向と糸のなす角を\(\theta\)とします。
また、図ではおおげさに描いていますが、実際はわずかにしか引いていないので、おもりはほとんど\(x\)軸上を運動することになります。
以上から、おもりは\(x\)軸上を運動し、鉛直方向には静止する(つりあう)と考えて運動方程式とつりあいの式を立てると
\(\displaystyle{\begin{eqnarray}&&{\bf{おもりをわずかに振る}}\\\\{\Leftrightarrow}&&{\bf{おもりはx軸からほとんど離れない}}\\\\{\Leftrightarrow}&&{\bf{おもりはx軸上で横方向に振動する}}\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}T\cos\theta=mg {\bf{(上下のつりあい)}}\\\\ma=-T\sin\theta {\bf{水平方向の運動 方程式}}\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}T=\frac{mg}{\cos\theta}\\ma=-\frac{mg}{\cos\theta}×\sin\theta=-mg\tan\theta\end{array}\right.\end{eqnarray}}\)
よって、
\(\displaystyle{ma=-mg\tan\theta}\)
※ちなみに、\(\theta\)が非常に小さいとき、
\(\tan\theta≒\sin\theta≒\theta\)
と近似ができる。
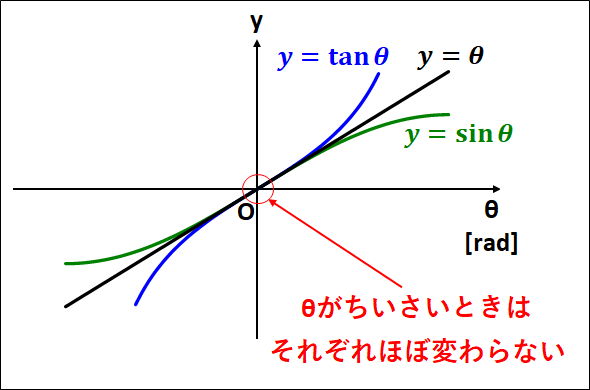
この近似を用いると以下のようになる。
\(\displaystyle{\begin{eqnarray}&& ma=-mg\tan\theta\\\\&&\left(\begin{array}{l}{\Leftrightarrow}ma≒-mg\tan\theta\\\\{\Leftrightarrow}a≒-g\tan\theta\end{array}\right)\end{eqnarray}}\)
\(\tan\theta\)は下図のようになります。
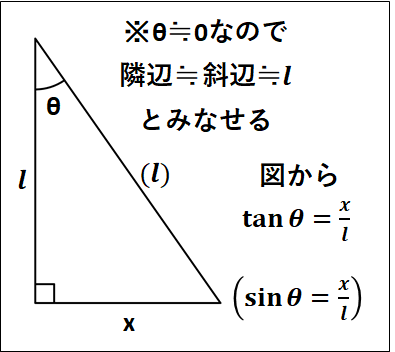
これを用いて、さらに運動方程式を変形していくと、
\(\displaystyle{\begin{eqnarray}&&ma=-mg\tan\theta\\\\{\Leftrightarrow}&&ma≒-mg\frac{x}{l}\\\\{\Leftrightarrow}&&a≒-\frac{g}{l}x\end{eqnarray}}\)
以上から、
角振動数:
\(\displaystyle{\omega=\frac{g}{l}}\)
振動中心:
\(x=0\)
振幅:
\(|A-0|=A\)
であることが分かります。
また、単振動の形は(正→0→負→0→正)のように変化していくので、\(+\cos\)形になります。
よって、変位の式は
\(\displaystyle{\begin{eqnarray}x&=&A\cos\omega{t}\\\\&=&A\cos\left(\sqrt{\frac{g}{l}}t\right)\\\\&=&A\cos\left(2\pi\frac{t}{\textcolor{blue}{2\pi\sqrt{\frac{l}{g}}}}\right)\end{eqnarray}}\)
これより、周期は\(T\)は\(2\pi{t}\)の分母なので、
\(\displaystyle{T=2\pi\sqrt{\frac{l}{g}}}\)
となります。
また、変位の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}v&=&-A\omega\sin\omega{t}\\\\&=&-A\sqrt{\frac{g}{l}}\sin\left(\sqrt{\frac{g}{l}}t\right)\end{eqnarray}}\)
さらに速度の式を\(t\)で微分して
\(\displaystyle{\begin{eqnarray}a&=&-A{\omega}^2\cos\omega{t}\\\\&=&-A\frac{g}{l}\cos\left(\sqrt{\frac{g}{l}}t\right)\end{eqnarray}}\)
以上から、\(x,v,a\)の関係グラフは以下のようになります。
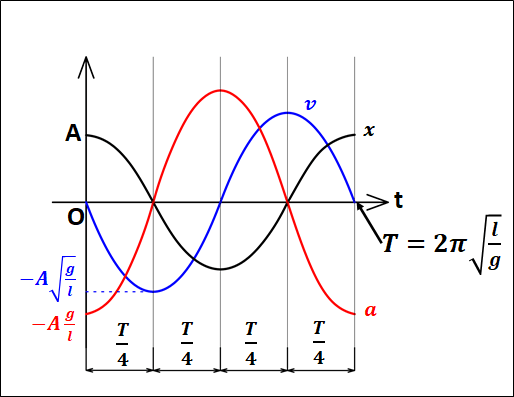
上記から、振り子の周期において\(2\pi\)と\(g\)は定数となります。
よって、単振り子の周期は振幅が小さければ振り子の長さ\(l\)だけで決まることになります。
このように、周期が振幅によらずに振り子の長さだけで決まることを、\(\textcolor{red}{\bf{振り子の等時性}}\)といいます。
一般解を用いると、
運動方程式から、
角振動数
\(\displaystyle{\omega=\sqrt{\frac{g}{l}}}\)
振動中心
\(x=0\)
振幅
\(A\)
がわかります。
よって、一般解から
\(\displaystyle{x=A'\cos\omega{t}+B'\sin\omega{t}}\)
\(\displaystyle{\begin{eqnarray}v&=&\frac{dx}{dt}\\\\&=&-A'\omega\sin\omega{t}+B'\omega\cos\omega{t}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}a&=&\frac{dv}{dt}\\\\&=&-A'{\omega}^2\cos\omega{t}-B'{\omega}^2\sin\omega{t}\end{eqnarray}}\)
初期条件\(t=0\)のとき、\(x=A , v=0\)を上式に代入して
\(A'=A , B'=0\)
と決まります。
これを元に戻すと先ほどの同様の式
\(\displaystyle{x=A\cos\omega{t}}\)
\(\displaystyle{v=-A\omega\sin\omega{t}}\)
\(\displaystyle{a=-A{\omega}^2\cos\omega{t}}\)
が得られます。
8.単振動のエネルギー
振動する物体の時間による位置が
\(\displaystyle{x=A\cos\omega{t}}\)
で表されているとします。
※
運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&a=-\frac{k}{m}x\end{eqnarray}}\)
より
\(\displaystyle{\omega=\sqrt{\frac{k}{m}}}\)
このとき、
\(\displaystyle{x=A\cos\omega{t}}\)
上式を\(t\)で微分して
\(\displaystyle{v=-A\omega\sin\omega{t}}\)
速度の式を\(t\)で微分して
\(\displaystyle{a=-A{\omega}^2\cos\omega{t}}\)
ここで、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&{\bf{単振動のエネルギー}}\\\\=&&{\bf{物体の運動エネルギー+ばねの弾性力による位置 エネルギー}}\end{eqnarray}}}\)
となります。
ここから、
\(\underline{\bf{教科書的に…}}\)
単振動のエネルギー(エネルギーの和)は、物体の運動エネルギーとばねの弾性力による位置エネルギーの和なので、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&{\bf{単 振動のエネルギー}}\\\\=&&{\bf{物体の運動エネルギー+ばねの弾性力による位置 エネルギー}}\\\\&&=\frac{1}{2}m\textcolor{red}{v}^2+\frac{1}{2}k\textcolor{red}{x}^2\end{eqnarray}}}\)
上式の形から、\(\textcolor{red}{v}\)と\(\textcolor{red}{x}\)に単振動の式を代入できます。
実際に代入すると
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}m\textcolor{red}{v}^2+\frac{1}{2}k\textcolor{red}{x}^2\\\\=&&\frac{1}{2}m(\textcolor{red}{-A\omega\sin\omega{t}})^2+\frac{1}{2}k(\textcolor{red}{A\cos\omega{t}})^2\\\\=&&\frac{1}{2}mA^2{\omega}^2\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t}\\\\=&&\frac{1}{2}mA^2\frac{k}{m}\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t} \left(∵\omega=\sqrt{\frac{k}{m}}\right)\\\\=&&\frac{1}{2}kA^2\sin^2\omega{t}+\frac{1}{2}kA^2\cos^2\omega{t}\\\\=&&\frac{1}{2}kA^2(\sin^2\omega{t}+\cos^2\omega{t})\\\\=&&\frac{1}{2}kA^2 (一定)\end{eqnarray}}}\)
また、
\(\displaystyle{{\omega}^2=\frac{k}{m}{\Leftrightarrow}k=m{\omega}^2}\)
から、
\(\displaystyle{\frac{1}{2}kA^2=\frac{1}{2}(m{\omega}^2)A^2 (一定)}\)
また、
\(\displaystyle{\omega=\frac{2\pi}{T}=2\pi{f}}\)
を用いると、
\(\displaystyle{\begin{eqnarray}&&\frac{1}{2}\left\{m(2\pi{f})^2\right\}A^2\\\\=&&2m{\pi}^2f^2A^2 (一定)\end{eqnarray}}\)
以上から、単振動のエネルギーは時間に関係なく、一定になります。
\(\underline{\bf{大学的に…}}\)
\(\textcolor{green}{\bf{エネルギー積 分}}\)
運動方程式の両辺に\(v\)を掛けて
\(\displaystyle{\begin{eqnarray}&&ma=-kx\\\\{\Leftrightarrow}&&m\textcolor{red}{v}a=-kx\textcolor{red}{v}\end{eqnarray}}\)
ここで、速度と加速度の定義
\(\displaystyle{\textcolor{red}{v=\frac{dx}{dt} , a=\frac{dv}{dt}}}\)
から、運動方程式の変形を続けて
\(\displaystyle{\begin{eqnarray}&&m\textcolor{red}{v}a=-kx\textcolor{red}{v}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=-kx\frac{dx}{dt}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}+kx\frac{dx}{dt}=0\end{eqnarray}}\)
ここで、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\frac{1}{2}mv^2&=&\frac{dv}{dt}\frac{d}{dv}\frac{1}{2}mv^2\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\frac{1}{2}kx^2&=&\frac{dx}{dt}\frac{d}{dx}\frac{1}{2}kx^2\\\\&=&kx\frac{dx}{dt}\end{eqnarray}}\)
から、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}+kx\frac{dx}{dt}=0\\\\=&&\frac{d}{dt}\left(\frac{1}{2}mv^2+\frac{1}{2}kx^2\right)=0\end{eqnarray}}\)
以上から、
\(\displaystyle{\frac{1}{2}mv^2+\frac{1}{2}kx^2}\)
は時間\(t\)で微分すると\(0\)になるので、定数となります。
すなわち、上式は時間によらずに一定になります。
※
エネルギー積分については、こちらの力学的エネルギー保存の法則も参考にしてください。
→仕事とエネルギー
