4.落下運動①
落下運動とは、落ちる物体の運動のことです。
これらの問題は、\(v-t\)グラフを描けば解けるのですが、そのために知っておかなけらばならないことがあります。
この記事では、\(v-t\)グラフを描く際の注意点と、落下運動の種類について解説していきます。
落下運動の具体的な問題の解き方については、別記事で練習問題を用意するので、そちらを参考にしてください。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.落下運動とは
落下運動とは、その名のとおり落ちる物体の運動のことです。
落下運動の問題を解く上では、\(v-t\)グラフが描ければ、加速度の定義式と\(v-t\)グラフの面積から解くことができますが、\(v-t\)グラフを描くために知っておかなければならないことがあります。
(\(v-t\)グラフについてはこちら→v-tグラフと等加速度直線運動)
下記が、落下運動する物体の\(v-t\)グラフを描く際の注意点になります。
\(\bf{①}\)
原点を決める。
原点は物体が運動をはじめたスタート地点にとる。
\(\bf{②}\)
軸を設定する。
正の方向は、初速度が正となる方向または、物体がこれから進むであろう方向にとる。
\(\bf{③}\)
重力加速度\(g=9.8m/s^2\)は\(v-t\)グラフの傾きを表し、下向きの方向である。
\(v-t\)グラフにおける重力加速度の正負は、設定した軸の正の方向と同じなら正、逆なら負とする。
軸の設定はどの向きを正にとっても良いのですが(問題によっては指定されている)、はじめは\(②\)のような向きにとると分かりやすいと思います。
これから、いくつかの落下運動をみていきますが、特に覚える必要はありません。(\(v-t\)グラフが描ければ解けるから)
ただし、運動の内容と\(v-t\)グラフが、どのように対応しているかは理解するようにしましょう。
また、図の中に静止している人を描いていますが、今後のために"物体の運動は静止している人からみたもの"であることを意識しておきましょう。
2.自由落下
自由落下とは、物体を静かに放した際の運動になります。
("静かに放す\(\Leftrightarrow\)初速度0m/s" のこと)
ビルの上で物体を静かに放す例を考えてみます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
先に述べた\(v-t\)グラフを描く際の注意点、\(①~③\)に注目してください。
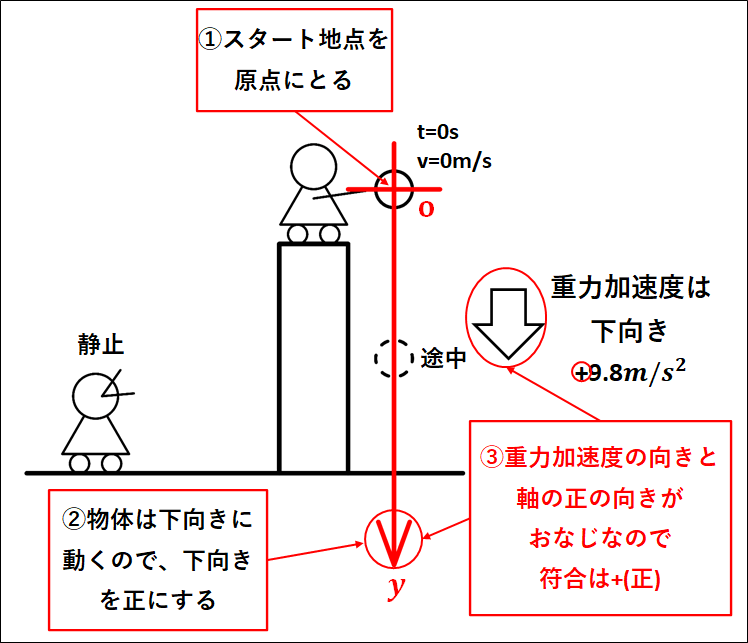
①物体はビルの上から落とされるので、ビルの上の落とされる位置が物体の原点となります。
②物体は落ちて下向きに運動するので、下向きを正にします。
③重力加速度は常に下向きで、今、軸の正の向きも下向きとしています。
重力加速度の向きと、軸の正の向きが同じなので、重力加速度の符合は正(+)になります。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=0m/s\)(静かに放すので初速度は\(0m/s\))。
重力加速度は、\(v-t\)グラフで扱った際の加速度と同じように\(v-t\)グラフの傾きを表します。
よって、\(v-t\)グラフは右上がりの直線となります。
(重力加速度は\(+9.8m/s^2\)という一定の値なので、グラフは直線となる(等加速度直線運動))
\(v-t\)グラフを図示すると以下のようになります。
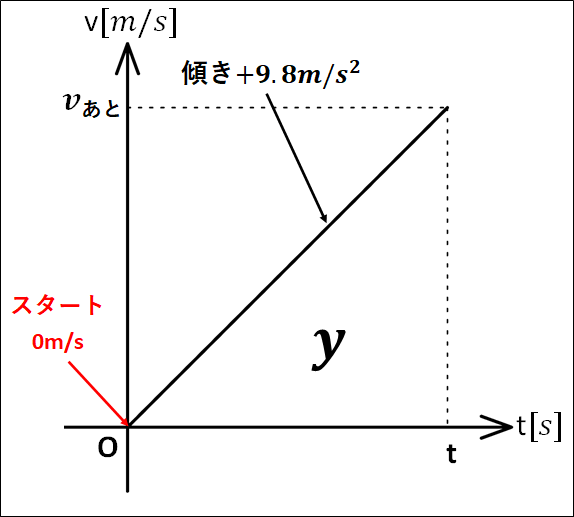
\(v-t\)グラフは手を放してから\(t\)秒後までを描いてあります。
図中の面積\(y\)はグラフが\(t\)軸よりも上にあるので正の面積であり、今、下向きを正にとっているので、物体が下向きに進んだ距離を表します。
(今までは\(x\)と表記していたが、縦方向(鉛直方向)の運動のため\(y\)と表示)
実際に問題を解く際には、与えられた情報と、この\(v-t\)グラフから面積や\(v_{\bf{あと}}\)などを求めていくことになります。
3.鉛直投げ下ろし
自由落下では物体を静かに放しましたが、鉛直投げ下ろしは、真下に向かって物体を投げたときの運動となります。
なので、自由落下との違いは初速度が\(0m/s\)ではないこととなります。
例として、ビルの上から物体を初速度\(v_{0}m/s\)で真下に投げ下ろすことを考えます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
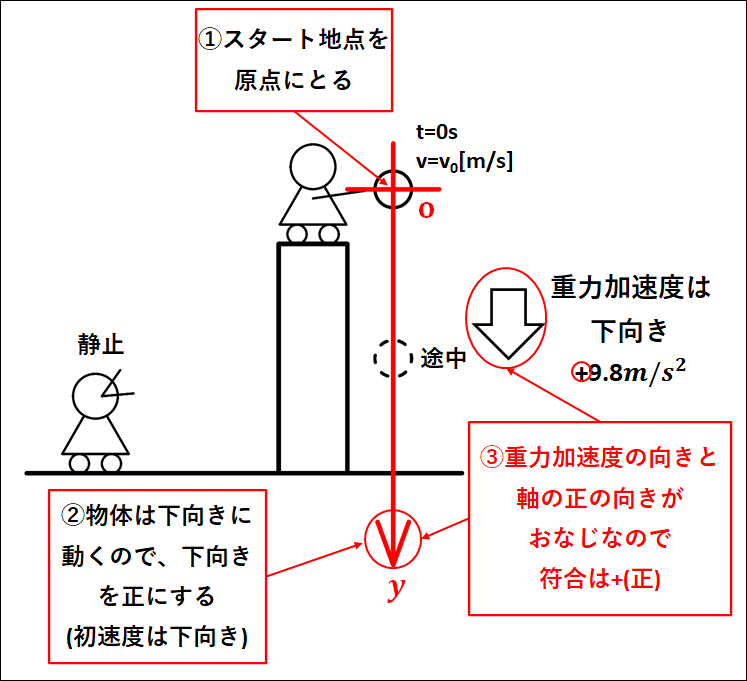
自由落下との図の違いは、\(t=0s\)での初速度が\(0m/s\)ではなく\(v_{0}[m/s]\)となっていることだけです。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=v_0[m/s]\)。
重力加速度は\(+9.8m/s^2\)と正の値なので、グラフの傾きは右上がりとなります。
\(v-t\)グラフを図示すると以下のようになります。
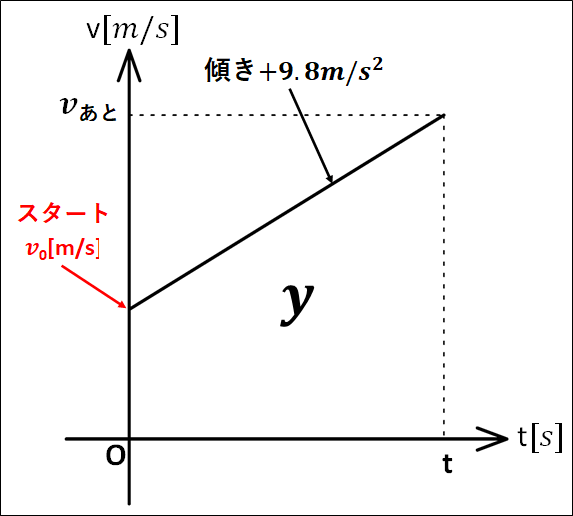
\(v-t\)グラフは物体を投げ下ろしてから\(t\)秒後までを描いてあります。
図中の面積\(y\)はグラフが\(t\)軸よりも上にあるので正の面積であり、今、下向きを正にとっているので、 物体が下向きに進んだ距離を表します。
4.鉛直投げ上げ
鉛直投げ上げは、物体を真上に投げたときの運動になります。
\(\textcolor{red}{\bf{○ポイント}}\)
→上に投げた物体は、最高点で一瞬止まり、その後落ちてくる!!
イメージ図を載せておきます。
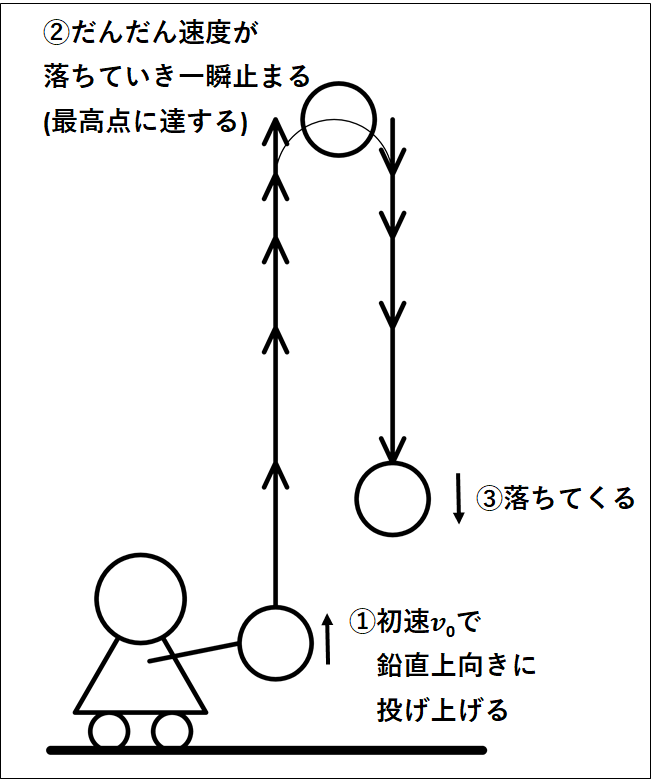
図では見やすくするために、物体が上がっているときと下がっているときをずらして描いていますが、実際には同一直線上を上がってから下がってくると考えてください。
投げ上げた直後は物体は速いですが、重力にひかれてだんだん遅くなっていきます。
その後、最高点で一瞬止まり(速度が\(0m/s\)になり)、その後落ちてきます。
落ちてくるときは、はじめは物体は遅いですが、だんだん速くなっていきます。
例として、物体を初速度\(v_0\)で投げ上げる場合を考えていきます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
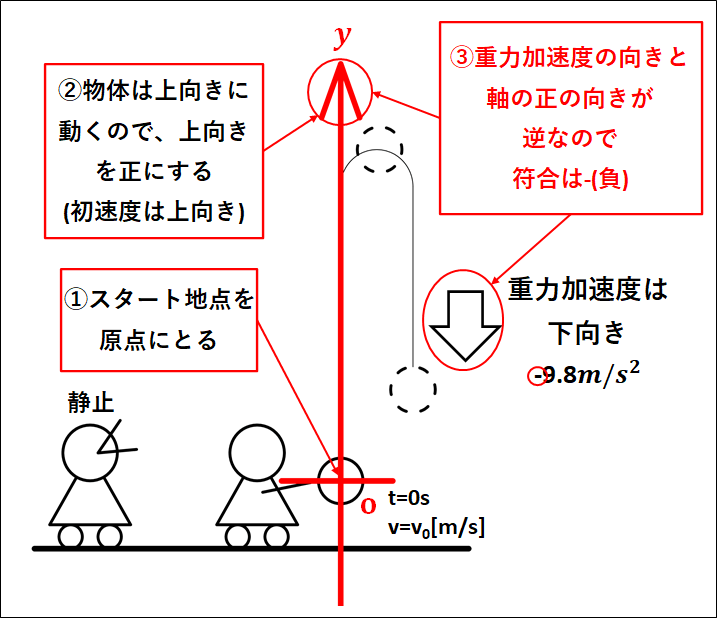
こちらも、物体は同一直線上を上がってから下がってくると考えてください。
①物体は投げ上げられて鉛直上向きに運動をはじめるので、投げ上げられる直前が原点となります。
②物体は投げ上げられて、鉛直上向きに運動するので上向きを正とします。
③重力加速度は常に下向きで、今、軸の正の向きは上向きとしています。
重力加速度の向きと、軸の正の向きが逆なので、重力加速度の符合は負(-)になります。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=v_0[m/s]\)
重力加速度は、\(v-t\)グラフの傾きを表しますが、今回は値が負なのでグラフは右下がりの直線になります。
\(v-t\)グラフを図示すると以下のようになります。
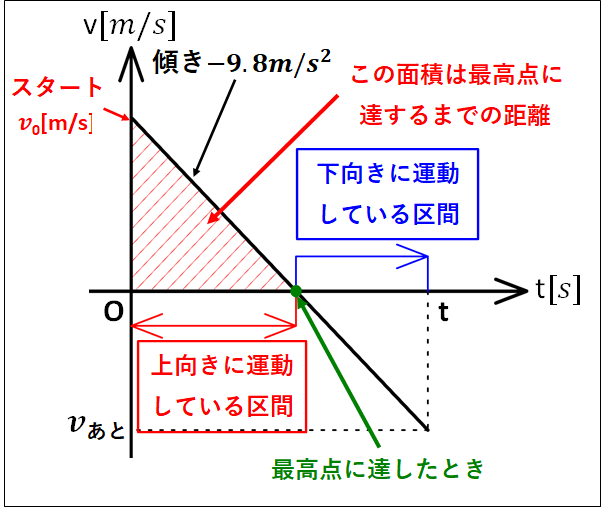
\(v-t\)グラフは物体を投げ下ろしてから\(t\)秒後までを描いてあります。
\(v-t\)グラフから、グラフの傾きが右下がりなので時間の経過とともに速度が初速度\(v_0\)からだんだん遅くなっていることが分かると思います。
そして、\(t\)軸とグラフが交わる点では速度\(0m/s\)となるので、ここが最高点に達する点となります。
グラフが\(t\)軸よりも上の部分は正の面積となります。
今、上向きを正としているので、正の面積は上向きに進んだ距離を表しています。
また、グラフが\(t\)軸よりも下側の部分は速度が負となっており、上向きを正としているので速度は下向きであることを表しています。
この部分の面積に関しては、負の面積となり、現在上向きを正としているので下向きに進んだ距離を表しています。
落下運動には他にも水平投射や斜方投射などがありますが、今後解説する運動方程式を学んでからの方が理解しやすいと思うので、運動方程式を学んだあとに解説します。
はてなブログ内関連記事
3-1.速度の合成と相対速度(補足解説と練習問題)
速度の合成と相対速度の記事で解説した内容の練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、速度の合成と相対速度の記事で解説していなかった補足内容があれば、この記事に載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.速度の合成
1-1.問題1
\(\underline{\bf{問題1}}\)
地面に対する速さが30m/分の動く床(ムービングウォーク)が右向きに動いている。
この上を、歩く速さが地面に対して70m/分の人が左向きに歩くとき、この人の地面に対する速度は何m/分か。
\(\underline{\bf{解答1}}\)
右向きを正とします。
動く床の地面に対する(から見た)速度を\(\textcolor{red}{v_{床}}\)、歩く人の地面に対する(から見た)速度を\(\textcolor{blue}{v_{人}}\)とするとこれらはそれぞれ
\(\textcolor{red}{v_{床}=+30m/分}\)
\(\textcolor{blue}{v_{人}=-70m/分}\)
となります。
求める地面に対する(から見た)動く床の上を歩く人の速度を\(\textcolor{green}{v}\)として速度ベクトルを図示すると、下図のようになります。
これより求めるベクトルは
\(\displaystyle{\begin{eqnarray}\textcolor{green}{v}&=&\textcolor{blue}{v_{人}}+\textcolor{red}{v_{床}}\\\\&=&\textcolor{blue}{-70m/分}+\textcolor{red}{(+30m/分)}\\\\&=&\textcolor{green}{-40m/分}\end{eqnarray}}\)
右向きを正としており、求めた速度の符合は負なので
\(\underline{{\bf{左向きに}}40m/分}\)
1-2.問題2
\(\underline{\bf{問題2}}\)
無風の状態ではまっすぐに17m/分の速さで飛ぶラジコン飛行機を風が吹いている中で飛ばすことを考える。
南向きに風が15m/分の速さで吹いている中を、真東の向きに飛ばし、東に160mのゴール地点に到着させるとき、どの向きにラジコン飛行機を飛ばせばよいか。
また、ラジコン飛行機を飛ばしてからゴール地点に到着するまでに要する時間は何分か。
\(\underline{\bf{解答2}}\)
風が吹いていないときにラジコン飛行機を真東の向きに飛ばすと、ラジコン飛行機はまっすぐにゴール地点に着きます。
風が南に吹いていると、ラジコン飛行機を真東に飛ばしたとしても、風に流されてしまいます。
なので、ラジコン飛行機を真東に飛ばすためには、角度をつけて飛ばす必要があります。
ラジコン飛行機と風の速度ベクトルを考えると、下図のようになります。
上図の直角三角形において、三平方の定理を用いると合成速度\(\textcolor{blue}{v}\)は
\(\displaystyle{\begin{eqnarray}&&\textcolor{red}{(17m/分)^2}=\textcolor{green}{(15m/分)^2}+\textcolor{blue}{v^2}\\\\{\Leftrightarrow}&&\textcolor{blue}{v^2}=\textcolor{blue}{(8.0m/分)^2}\end{eqnarray}}\)
これより、
\(\textcolor{blue}{v=8.0m/分}\)
真東に向かって、160mの距離を8m/分で進むので、ゴール地点に到着するまでの時間は
\(\displaystyle{\begin{eqnarray}{\bf{時間}}&=&160m÷8.0m/分\\\\&=&160m×\frac{分}{8.0m}\\\\&=&20分\end{eqnarray}}\)
よって、
\(\underline{20分}\)
角度は、速度ベクトルの直角三角形から\(\tan{\theta}\)を考えると
\(\displaystyle{\begin{eqnarray}\tan{\theta}&=&\frac{15}{8.0}\\\\&=&1.875\end{eqnarray}}\)
より、真東から北向きに\(\tan{\theta}=1.875\)を満たす\(\theta\)の向きにラジコンを飛ばせばよい。
※
三角関数表や関数電卓を用いると、
\(\theta≒62°\)
ぐらいとなります。
2.相対速度
2-1.問題1
\(\underline{\bf{問題1}}\)
東向きに13m/sで走行する自動車に対する、東向きに8.0m/sで走行する自転車および、西向きに4.0m/sで走行する自転車の相対速度を求めよ。
\(\underline{\bf{解答1}}\)
右向きを正とします。
問題文中の速度
→\(\textcolor{red}{\bf{地面からみた速度}}\)
(→\(\textcolor{red}{\bf{静止した人からみた速度}}\))
~に対する
→\(\textcolor{red}{\bf{~からみた}}\)
と読みかえます。
そうすると、それぞれの速度は
・東向きに13m/sで走行する自動車
→地面から見て+13m/s
・東向きに8.0m/sで走行する自転車
→地面から見て+8.0m/s
・西向きに4.0m/sで走行する自転車
→地面から見て-4.0m/s
となります。
また、
自動車に対する自転車の速度
→自動車からみた自転車の速度
を求めればよいことがわかります。
問題を解いていきます。
自動車に対する東向きに8.0m/sで走行する自転車の相対速度について、
i)ベクトル図で考えると
※ベクトルの長さは13m/sから8.0m/sを引いて
\(13m/s-8.0m/s=5.0m/s\)
となります。
いま東向きを正としており、求めるベクトルは負の方向を向いているので求める相対速度は
\(\underline{{\bf{西向きに}}5.0m/s}\)
です。
ii)v-tグラフで考えると
自動車の速度と自転車の速度の幅は5.0m/sで、矢印は下向きなので
-5.0m/s
となり、
\(\underline{{\bf{西向きに}}5.0m/s}\)
になります。
※
相対速度=相手の速度-自分の速度
を用いると
相手:自転車(+8.0m/s)
自分:自動車(+13m/s)
から
\(+8.0m/s-(+13m/s)=-5.0m/s\)
となる。
自動車に対する西向きに4.0m/sで走行する自転車の相対速度について、
こちらも同様にして考えて
i)ベクトル図で考えると
※ベクトルの長さは13m/sと4.0m/sを足して
\(13m/s+4.0m/s=17m/s\)
となります。
いま東向きを正としおり、求めるベクトルは負の方向を向いているので求める相対速度は
\(\underline{{\bf{西向きに}}17m/s}\)
です。
ii)v-tグラフで考えると
自動車の速度と自転車の速度の幅は17m/sで、矢印は下向きなので
-5.0m/s
となり、
\(\underline{{\bf{西向きに}}17m/s}\)
になります。
※
相対速度=相手の速度-自分の速度
を用いると
相手:自転車(-4.0m/s)
自分:自動車(+18m/s)
から
\(-4.0m/s-(+13m/s)=-17m/s\)
となる。
2-2.問題2
\(\underline{\bf{問題2}}\)
東向きに13m/sで走行する自動車に対する、南向きに13m/sで走行する自転車の相対速度を求めよ。
\(\underline{\bf{解答2}}\)
「~に対する」を「~からみた」と翻訳する点については、前問と同様です。
しかし今回は自動車と自転車が同一直線上を運動していないので、ベクトル図を用いて考えます。
自動車と自転車の速度ベクトルを図示すると、下図のようになります。
求める相対速度の大きさは、三平方の定理から
\(\displaystyle{\begin{eqnarray}\textcolor{green}{v^2}&=&\textcolor{red}{{13m/s}^2}+\textcolor{blue}{{13m/s}^2}\\\\&=&\textcolor{green}{{13\sqrt{2}m/s}^2}\end{eqnarray}}\)
これより、
\(\displaystyle{\begin{eqnarray}|v|&=&13\sqrt{2}\\\\&≒&18.4m/s\\\\&≒&18m/s\end{eqnarray}}\)
向きは、下図のように\(\theta\)を考えます。
上図から
\(\displaystyle{\begin{eqnarray}\tan{\theta}&=&\frac{13}{13}\\\\&=&1\end{eqnarray}}\)
これは有名角で\(\theta=45°\)となります。
※三角関数の有名角についてはこちら
→三角関数の定義と関係式
よって、図から向きは南西の方向となります。
以上から求める相対速度は
\(\underline{{\bf{南西の向きに}}18m/s}\)
となります。
はてなブログ内関連記事
3.速度の合成と相対速度
速度はベクトルなので、ベクトルの加法や減法のように計算することができます。
また、相対速度とはあるものから見た別のあるものの速度のことになります。
例えば、地面からみた電車の中にいる人の速度などがこれになります。
相対速度は\(v-t\)グラフやベクトル図などで捉えることができますが、これらについて解説していきます。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.速度の合成
速度は向きと大きさを持つベクトルなので、ベクトルの加法や減法のように計算することができます。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
例として、地面の上で静止している人と、動く床の上を歩く人を考えてみます。
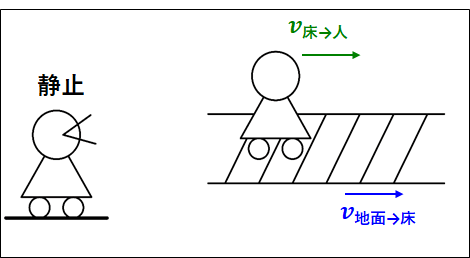
\(\textcolor{red}{\bf{静止している人(地面)から見て}}\)、床は速度\(\textcolor{blue}{v_{\bf{地面\to床}}}\)で動いているとし、床の上を歩く人は\(\textcolor{red}{\bf{床から見て}}\)速度\(\textcolor{green}{v_{\bf{床\to人}}}\)で歩いているとします。
このとき、静止している人(地面)から見た床の上を歩いている人の速度を\(v_{\bf{地面\to人}}\)とすると、
\(v_{\bf{地面\to人}}=\textcolor{blue}{v_{\bf{地面\to床}}}+\textcolor{green}{v_{\bf{床\to人}}}\)
となります。
ベクトルの計算なので、イメージは以下のようになります。
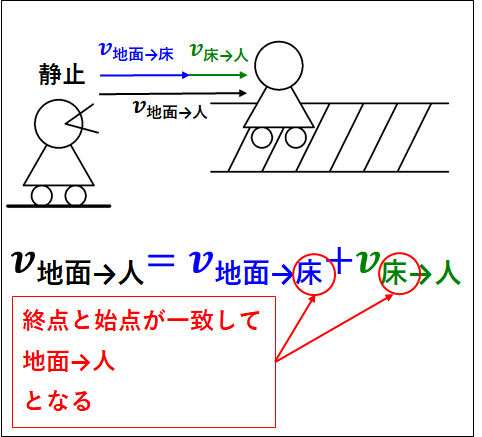
例えば、
\(\textcolor{blue}{v_{\bf{地面\to床}}=+5.0m/s}\)
\(\textcolor{green}{v_{\bf{床\to人}}=+3.0m/s}\)
とすると、静止している人(地面)から見た床の上を歩いている人の速度\(v_{\bf{地面\to人}}\)は、
\(\displaystyle{\begin{eqnarray}v_{\bf{地面\to人}}&=&\textcolor{blue}{v_{\bf{地面\to床}}}+\textcolor{green}{v_{\bf{床\to人}}}\\\\&=&\textcolor{blue}{+5.0m/s}+\textcolor{green}{(+3.0m/s)}\\\\&=&+8.0m/s\end{eqnarray}}\)
となります。
このように、2つの速度を合わせた速度を求めることを、\(\textcolor{red}{\bf{速度の合成}}\)といい、この合わされた速度を\(\textcolor{red}{\bf{合成速度}}\)といいます。
2.相対速度
速度というと、一般的には静止した人(地面)から見た速度のことを指します。
これに対して、あるものから見た別のあるものの速度を\(\textcolor{red}{\bf{相対速度}}\)といいます。
例として、静止している人と車に乗っている人、電車に乗っている人を考えてみます。
静止している人(地面)から見た車の速度を\(\textcolor{blue}{v_{\bf{車}}}\)、静止している人(地面)から見た電車の速度を\(\textcolor{green}{v_{\bf{電車}}}\)とします。
このとき、車に乗った人から見た電車の速度を
\(\textcolor{red}{\bf{"車に対する電車の相対速度"}}\)
といいます。
※
\(A\)\(\textcolor{red}{\underline{\bf{に対する}}}\)\(B\)の相対速度
では分かりにくいので
→\(A\)\(\textcolor{red}{\underline{\bf{から見た}}}\)\(B\)の相対速度
と言い換えると分かりやすいと思います。
次のベクトル図と\(v-t\)グラフの活用で、実際にどのように相対速度が表されるのかをみていきます。
3.ベクトル図とv-tグラフの活用
先述の静止している人(地面)と、車、電車の速度の関係を、ベクトル図と\(v-t\)グラフで捉えてみます。
なお、車と電車は同一直線上を右向きに運動しているとし、\(\textcolor{blue}{v_{\bf{車}}}\lt\textcolor{green}{v_{\bf{電車}}}\)のときの車に対する(車から見た)電車の相対速度を考えます。
この、車に対する(車から見た)電車の相対速度を\(\textcolor{red}{v_{\bf{車\to電車}}}\)とします。
\(\bf{i)ベクトル図}\)
ベクトルは向きと大きさを持ち、向きを矢印の向きで、大きさを矢印の長さで表します。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
今回、車と電車は右向きに動いているので、右向きを正として図示すると下図のようになります。(原点は静止している人)
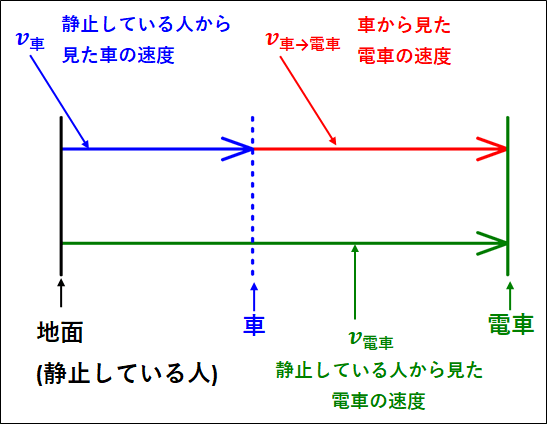
ベクトルの向きに注意しなけらばなりませんが、赤のベクトルは緑のベクトルから青のベクトルを引いたものとなるので、ベクトル図から赤色の車に対する(車から見た)電車の相対速度\(\textcolor{red}{v_{\bf{車\to電車}}}\)は、
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
となります。
または、図中の緑のベクトルが、青と赤のベクトルを足したものなので
\(\textcolor{blue}{v_{\bf{車}}}+\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}\)
から、\(\textcolor{blue}{v_{\bf{車}}}\)を右辺に移項させて
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
と考えると分かりやすいかもしれません。
\({\bf{ii)}}v-t{\bf{グラフ}}\)
\(v-t\)グラフは下図のようになります。\(v=0\)のときが静止している人(地面)の速度となります。
(\(v-t\)グラフについてはこちらも参考にしてください。→v-tグラフと等加速度直線運動)
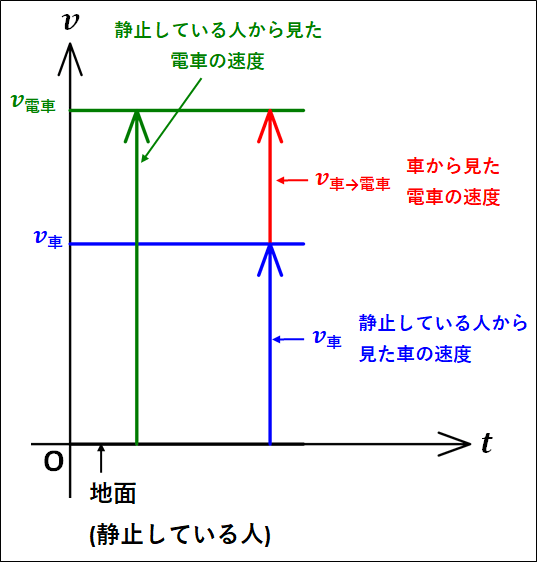
\(v-t\)グラフから、ベクトル図のときと同様にして車に対する(車から見た)電車の相対速度\(\textcolor{red}{v_{\bf{車\to電車}}}\)は
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
となります。
\(v-t\)グラフは速度の正負は表現できるので、同一直線上を運動する物体については有効です。
(北と南、東と西方向など)
一方、速度ベクトルが同一直線上になく、斜め方向などの場合(例えば南と北東方向など)はベクトル図が有効となってきます。
こういった同一直線上にない速度をベクトル図で扱うには、簡単なベクトルの知識と三角関数の知識が必要となってきます。
(三角関数についてはこちらも参考にしてください→三角関数の定義と関係式)
一般に、\(A\)に対する\(B\)の相対速度\(v_{\bf{AB}}\)は、\(A\)の地面に対する速度を\(v_{\bf{A}}\)、\(B\)の地面に対する速度を\(v_{\bf{B}}\)とすると、
\(v_{\bf{AB}}=v_{\bf{B}}-v_{\bf{A}}\)(相手の速度-自分の速度)
で表されます。
上記式中の速度は、ベクトルなので成分計算をする場合は、符合も含めたものであることに注意しなければなりません。
例として、\(A\)さんが西に\(1.5m/s\)、\(B\)さんが東に\(1.0m/s\)で移動しているときを考えます。
西と東のどちらを正としてもよいですが、とりあえず東を正としておきます。
このとき、\(A\)さんと\(B\)さんのそれぞれの地面に対する速度を\(v_{\bf{A}}\)と\(v_{\bf{B}}\)とすると、東を正としているので
\(v_{\bf{A}}=-1.5m/s\)
\(v_{\bf{B}}=+1.0m/s\)
となります。
このときの、\(A\)さんに対する(\(A\)さんから見た)\(B\)さんの速度\(v_{\bf{AB}}\)は
\(\displaystyle{\begin{eqnarray}v_{\bf{AB}}&=&v_{\bf{B}}-v_{\bf{A}}\\\\&=&(+1.0m/s)-(-1.5m/s)\\\\&=&+2.5m/s\end{eqnarray}}\)
したがって、上記状況のとき\(A\)さんから見ると\(B\)さんは東へ\(2.5m/s\)の速さで移動しているように見えるということになります。(東を正としているので)
また、単に速度というときには、地面に対する速度のことを指しています。
\(\textcolor{red}{\bf{○ポイント}}\)
・\(A\)に対する\(B\)の相対速度は、\(A\)から見た\(B\)の相対速度と言い換えるとわかりやすい。
・\(\left\{\begin{eqnarray}&&\bf{○ベクトル図}\\&&\bf{○v-tグラフ}\end{eqnarray}\right.\bf{の利用}\)
はてなブログ内関連記事
2-1.v-tグラフと等加速度直線運動(補足解説と練習問題)
v-tグラフと等加速度直線運動の記事で解説した内容の練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、v-tグラフと等加速度直線運動の記事で解説していなかった補足内容があれば、この記事に載せています。
この記事を通して、"等加速度直線運動の公式"と呼ばれるものを用いなくても、問題が解けるとということを味わってください。
加速度の定義式と、v-tグラフの面積を求める式のみで解くことができます。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
- 1.v-tグラフの作成練習
- 2.s-tグラフからv-tグラフへの変換
- 3.グラフの変換
- 4.平均の加速度
- 5.等加速度直線運動とv-tグラフの利用
- 6.記録タイマー
- 7.v-tグラフにおける変位と移動距離
1.v-tグラフの作成練習
1-1.問題1
\(\underline{\bf{問題1}}\)
静止している物体が、右向きの加速度\(5.0m/s^2\)で\(5.0\)秒間移動したときの変位はどちら向きに何\(m\)か。
\(\underline{\bf{解答1}}\)
物体は右向きに運動するので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき静止(0m/s)
あと:t=4.0sのとき\(v_{あと}\)[m/s]
右向きの加速度\(5.0m/s^2\)
→\(+5.0m/s^2\)(右向きを正としているので符合は正)
また、加速度はv-tグラフの傾きを表すので、傾きは\(+5.0m/s^2\)と右上がりとなります。
v-tグラフの面積は変位(\(x\))を表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&5.0m/s^2=\frac{v_{あと}-0m/s}{5.0s-0s}\\\\{\Leftrightarrow}&&v_{あと}=25m/s\end{eqnarray}}\)
※
変位・速度・加速度の定義式についてはこちら
→変位・速度・加速度
v-tグラフの面積から、三角形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}{\bf{変位}}x&=&5.0s×v_{あと}×\frac{1}{2}\\\\&=&5.0s×25m/s×\frac{1}{2}\\\\&=&+62.5m\\\\&≒&63m\end{eqnarray}}\)
よって求める変位は、右向きを正としているので
\(\underline{{\bf{右向きに}}63m}\)
1-2.問題2
\(\underline{\bf{問題2}}\)
右向きの速さ2.0m/sで進んでいた物体が、右向きの加速度\(2.0m/s^2\)の運動をはじめ、右側に15m移動した。
このときの、物体の速度はどちら向きに何m/sか。
\(\underline{\bf{解答2}}\)
物体は右向きに運動するので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき右向きの速さ2.0m/s
→t=0sのとき+2.0m/s(右向き正なので符合は正)
あと:\(t=t_{あと}\)のとき\(v_{あと}\)[m/s]
右向きの加速度\(2.0m/s^2\)
→\(+2.0m/s^2\)(右向きを正としているので符合は正)
また、加速度はv-tグラフの傾きを表すので、傾きは\(+2.0m/s^2\)と右上がりとなります。
v-tグラフの面積は変位15mを表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&2.0m/s^2=\frac{v_{あと}-(+2.0m/s)}{t_{あと}-0s}\\\\{\Leftrightarrow}&&v_{あと}=2.0t+2.0m/s \cdots①\end{eqnarray}}\)
v-tグラフの面積から、台形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}&&15m=(2.0m/s+v_{あと})×t_{あと}×\frac{1}{2}\\\\{\Leftrightarrow}&&30m=(2.0m/s+v_{あと})×t_{あと} \cdots②\end{eqnarray}}\)
①を②に代入して
\(\displaystyle{\begin{eqnarray}&&30m=\left\{2.0m/s+(2.0t_{あと}+2.0m/s)\right\}×t_{あと}\\\\{\Leftrightarrow}&&30m=(4.0m/s+2.0t_{あと})×t_{あと}\\\\{\Leftrightarrow}&&2.0t_{あと}^2+4.0t_{あと}-30=0\\\\{\Leftrightarrow}&&t_{あと}^2+2.0t_{あと}-15=0\\\\{\Leftrightarrow}&&(t_{あと}+5)(t_{あと}-3)=0\end{eqnarray}}\)
v-tグラフから、\(t_{あと}\gt0\)より
\(t_{あと}\)=3s
これを①に代入して、
\(\displaystyle{\begin{eqnarray}v_{あと}&=&2.0×3m/s+2.0m/s\\\\&=&+8.0m/s\end{eqnarray}}\)
よって求める速度は、右向きを正としているので
\(\underline{{\bf{右向きに}}8.0m/s}\)
1-3.問題3
静止している物体が、右向きの加速度\(3.0m/s^2\)の運動をはじめ、右向きの速さ\(6.0m/s\)になった。
この間の変位はどちら向きに何\(m\)か。
\(\underline{\bf{解答3}}\)
物体は右向きに運動するので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき静止(0m/s)
あと:\(t=t_{あと}\)のとき右向きの速さ6.0m/s
→\(t=t_{あと}\)のとき+6.0m/s(右向きを正としているので符合は正)
右向きの加速度\(3.0m/s^2\)
→\(+3.0m/s^2\)(右向きを正としているので符合は正)
また、加速度はv-tグラフの傾きを表すので、傾きは\(+3.0m/s^2\)と右上がりとなります。
v-tグラフの面積は変位(\(x\))を表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&3.0m/s^2=\frac{6.0m/s-0m/s}{t_{あと}-0s}\\\\{\Leftrightarrow}&&t_{あと}=2.0s\end{eqnarray}}\)
v-tグラフの面積から、三角形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}{\bf{変位}}x&=&t_{あと}×6.0m/s×\frac{1}{2}\\\\&=&2.0s×6.0m/s×\frac{1}{2}\\\\&=&+6.0m\end{eqnarray}}\)
よって求める変位は、右向きを正としているので
\(\underline{{\bf{右向きに}}6.0m}\)
1-4.問題4
\(\underline{\bf{問題4}}\)
右向きの速さ2.0m/sで進んでいた物体が、右向きの加速度\(2.0m/s^2\)の運動をはじめ、右向きの速さ6.0m/sになった。
この間の変位は、どちら向きに何mか。
\(\underline{\bf{解答4}}\)
物体は右向きに運動するので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき右向きの速さ2.0m/s
→t=0sのとき+2.0m/s(右向き正なので符合は正)
あと:\(t=t_{あと}\)のとき右向きの速さ6.0m/s
→\(t=t_{あと}\)のとき+6.0m/s(右向き正なので符号は正)
右向きの加速度\(2.0m/s^2\)
→\(+2.0m/s^2\)(右向きを正としているので符合は正)
また、加速度はv-tグラフの傾きを表すので、傾きは\(+2.0m/s^2\)と右上がりとなります。
v-tグラフの面積は変位(\(x\))を表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&2.0m/s^2=\frac{6.0m/s-(+2.0m/s)}{t_{あと}-0s}\\\\{\Leftrightarrow}&&t_{あと}=2.0s\end{eqnarray}}\)
v-tグラフの面積から、台形の面積を求める式を用いて
\(\displaystyle{\begin{eqnarray}{\bf{変位}}x&=&(2.0m/s+6.0m/s)×t_{あと}×\frac{1}{2}\\\\&=&(2.0m/s+6.0m/s)×2.0s×\frac{1}{2}\\\\&=&+8.0m\end{eqnarray}}\)
よって求める変位は、右向きを正としているので
\(\underline{{\bf{右向きに}}8.0m}\)
1-5.問題5(難)
\(\underline{\bf{問題5(難)}}\)
右向きの速さ8.0m/sで進んでいた物体が、一定の加速度の運動をはじめ、右側に13m移動して、左向きの速さ5.0m/sになった。
加速度はどちら向きに何\(m/s^2\)か。
\(\underline{\bf{解答5}}\)
物体ははじめ、右向きに運動しているので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき右向きの速さ8.0m/s
→t=0sのとき+8.0m/s(右向き正なので符合は正)
あと:\(t=t_{あと}\)のとき左向きの速さ5.0m/s
→\(t=t_{あと}\)のとき-5.0m/s(右向き正なので符号は負)
一定の加速度
→v-tグラフの傾きは直線
右側に13m移動
→変位は+13m(右向き正なので符号は正)
v-tグラフの面積は変位+13mを表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&a[m/s^2]=\frac{-5.0m/s-(+8.0m/s)}{t_{あと}-0s}\\\\{\Leftrightarrow}&&a[m/s^2]=\frac{-13m/s}{t_{あと}} \cdots①\end{eqnarray}}\)
変位+13mは、
なので、
\(\displaystyle{\begin{eqnarray}&&13m=8.0m/s×t_{あと}-|\frac{1}{2}t_{あと}×13m/s|\\\\{\Leftrightarrow}&&13m=8.0m/s×t_{あと}-\frac{13}{2}m/s×t_{あと}\\\\{\Leftrightarrow}&&26m=16m/s×t_{あと}-13m/s×t_{あと}\\\\{\Leftrightarrow}&&26m=3m/s×t_{あと}\\\\{\Leftrightarrow}&&t_{あと}=\frac{26}{3}s \cdots②\end{eqnarray}}\)
②を①に代入して
\(\displaystyle{\begin{eqnarray}a&=&\frac{-13m/s}{\frac{26}{3}s}\\\\&=&\frac{-13×3m/s}{26s}\\\\&=&-\frac{3}{2}m/s^2\\\\&=&-1.5m/s^2\end{eqnarray}}\)
よって求める加速度は、右向きを正としており、求めた加速度の符号は負なので
\(\underline{{\bf{左向きに}}1.5m/s^2}\)
\(\underline{\bf{<考察>}}\)
v=0m/sのときの時刻をt'とすると、v-tグラフは下図のようになります。
t'を求めていきます。
正の部分の三角形に注目して、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-1.5m/s^2=\frac{0m/s-(+8.0m/s)}{t^{\prime}-0s}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{-8.0m/s}{-1.5m/s^2}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{16}{3}s\end{eqnarray}}\)
正の部分の面積は
\(\displaystyle{\begin{eqnarray}t^{\prime}×8.0m/s×\frac{1}{2}&=&\frac{16}{3}s×8.0m/s×\frac{1}{2}\\\\&=&\frac{64}{3}m\end{eqnarray}}\)
以上より、正の方向(右向き)に進んだ距離は
\(\displaystyle{\textcolor{red}{\frac{64}{3}m}}\)
となります。
次に負の部分の三角形の辺の長さは、下図のようになります。
よって、負の部分の面積は
\(\displaystyle{\begin{eqnarray}&&(t_{あと}-t^{\prime})×5.0m/s×\frac{1}{2}\\\\=&&\left(\frac{26}{3}s-\frac{16}{3}s\right)×5.0m/s×\frac{1}{2}\\\\&&=\frac{10}{3}s×5.0m/s×\frac{1}{2}\\\\&&=\frac{25}{3}m\end{eqnarray}}\)
以上より、負の方向(左向き)に進んだ距離は
\(\displaystyle{\textcolor{blue}{\frac{25}{3}m}}\)
となります。
※
あとの速度\(-5.0m/s\)を用いると、面積は
\(\displaystyle{-\frac{25}{3}m}\)
と負になる。
これは、右向きが正なので、負の向きである左向きに\(\frac{25}{3}m\)ということを意味しています。
以上から、状況を整理すると
はじめ:
右向きに8.0m/s
途中:
\(0~\frac{16}{3}s\)の間に、右向きに\(\frac{52}{3}m\)進んで、その後左向きに方向転換する。
\(\frac{16}{3}s~\frac{26}{3}s\)の間に左向きに\(\frac{25}{3}m\)進んで、左向きの速さ5.0m/sになる。
イメージは、下図のようになります。
1-6.問題6(難)
\(\underline{\bf{問題6(難)}}\)
右向きの速さ2.0m/sで進んでいた物体が、一定の加速度の運動をはじめ、左側に4.0m移動して、左向きの速さ6.0m/sになった。
加速度はどちら向きに何\(m/s^2\)か。
\(\underline{\bf{解答6}}\)
物体ははじめ、右向きに運動しているので、右向きを正とします。
はじめとあとの情報を整理すると
はじめ:t=0sのとき右向きの速さ2.0m/s
→t=0sのとき+2.0m/s(右向き正なので符合は正)
あと:\(t=t_{あと}\)のとき左向きの速さ6.0m/s
→\(t=t_{あと}\)のとき-6.0m/s(右向き正なので符号は負)
一定の加速度
→v-tグラフの傾きは直線
左側に4.0m移動
→変位は-4.0m(右向き正なので符号は負)
\(\textcolor{red}{\bf{注意!!}}\)
問題5と同様の方法で解いていきますが、変位が左側に4.0mであることから符号は負となることに注意。
v-tグラフの面積は変位-4.0mを表すので、v-tグラフは下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&a[m/s^2]=\frac{-6.0m/s-(+2.0m/s)}{t_{あと}-0s}\\\\{\Leftrightarrow}&&a[m/s^2]=\frac{-8.0m/s}{t_{あと}} \cdots①\end{eqnarray}}\)
変位-4.0mは、
なので、
\(\displaystyle{\begin{eqnarray}&&-4.0m=2.0m/s×t_{あと}-|\frac{1}{2}t_{あと}×8.0m/s|\\\\{\Leftrightarrow}&&-4.0m=2.0m/s×t_{あと}-4.0m/s×t_{あと}\\\\{\Leftrightarrow}&&-4.0m=-2.0m/s×t_{あと}\\\\{\Leftrightarrow}&&t_{あと}=2.0s \cdots②\end{eqnarray}}\)
②を①に代入して
\(\displaystyle{\begin{eqnarray}a&=&\frac{-8.0m/s}{2.0s}\\\\&=&-4.0m/s^2\end{eqnarray}}\)
よって求める加速度は、右向きを正としており、求めた加速度の符号は負なので
\(\underline{{\bf{左向きに}}4.0m/s^2}\)
\(\underline{\bf{<考察>}}\)
v=0m/sのときの時刻をt'とすると、v-tグラフは下図のようになります。
t'を求めていきます。
正の部分の三角形に注目して、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-4.0m/s^2=\frac{0m/s-(+2.0m/s)}{t^{\prime}-0s}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{1}{2}s\\\\{\Leftrightarrow}&&t^{\prime}=0.5s\end{eqnarray}}\)
正の部分の面積は
\(\displaystyle{\begin{eqnarray}t^{\prime}×2.0m/s×\frac{1}{2}&=&0.5s×2.0m/s×\frac{1}{2}\\\\&=&+0.5m\end{eqnarray}}\)
以上より、正の方向(右向き)に進んだ距離は
\(\displaystyle{\textcolor{red}{+0.5m}}\)
となります。
次に負の部分の三角形の辺の長さは、下図のようになります。
よって、負の部分の面積は
\(\displaystyle{\begin{eqnarray}&&(t_{あと}-t^{\prime})×6.0m/s×\frac{1}{2}\\\\=&&(2.0s-0.5s)×6.0m/s×\frac{1}{2}\\\\=&&+4.5m\end{eqnarray}}\)
以上より、負の方向(左向き)に進んだ距離は
\(\displaystyle{\textcolor{blue}{4.5m}}\)
となります。
※
あとの速度\(-6.0m/s\)を用いると、面積は
\(\displaystyle{-4.5m}\)
と負になる。
これは、右向きが正なので、負の向きである左向きに4.5mということを意味しています。
以上から、状況を整理すると
はじめ:
右向きに2.0m/s
途中
0s~0.5sの間に、右向きに0.5m進んで、その後左向きに方向転換する。
0.5s~2.0sの間に左向きに4.5m進んで、左向きの速さ6.0m/sになる。
イメージは、下図のようになります。
2.s-tグラフからv-tグラフへの変換
\(\underline{\bf{問題}}\)
次の位置s[m]と時間t[s]の関係を表したs-tグラフのように運動している物体がある。
この物体の速度v[m/s]と時間t[s]の関係を表すv-tグラフはどのようになるか。
\(\underline{\bf{解答}}\)
位置s[m]と速度v[m/s]の関係を表す式は、速度の定義式
\(\displaystyle{\textcolor{green}{\overline{V}=\frac{s_{あと}-s_{はじめ}}{t_{あと}-t{はじめ}}}}\)
となります。
上記の関係式を用いると、
○0~2.0sの間
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{+60m-0m}{2.0s-0s}\\\\&=&+30m/s\end{eqnarray}}\)
○2.0s~5.0sの間
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{+60m-(+60m)}{5.0s-2.0s}\\\\&=&\frac{0m}{3.0s}\\\\&=&0m/s\end{eqnarray}}\)
以上から、s-tグラフとv-tグラフを縦に並べて描くと、下図のようになります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・グラフの活用
→v-tグラフ(速度-時間グラフ)が基本のグラフ
→(変換)\(s-t\)グラフ(位置-時間グラフ)
→(変換)\(a-t\)グラフ(加速度-時間グラフ)
3.グラフの変換
\(\underline{\bf{問題}}\)
x軸上を次の\(v-t\)グラフのように運動している物体がある。
この物体の\(a-t\)グラフと\(x-t\)グラフはどのようになるか。
ただしt=0のときの物体の位置をx=0とする。
\(\underline{\bf{解答}}\)
○加速度について
加速度と速度の関係式は、加速度の定義式
\(\displaystyle{\textcolor{green}{a=\frac{v_{あと}-v_{はじめ}}{t_{あと}-t{はじめ}}}}\)
になります。
これを用いると、
\(・0s{\le}t{\le}10s\)のとき
\(\displaystyle{\begin{eqnarray}a&=&\frac{12m/s-0m/s}{10s-0s}\\\\&=&1.2m/s^2\end{eqnarray}}\)
\(・10s{\le}t{\le}20s\)のとき
\(\displaystyle{\begin{eqnarray}a&=&\frac{12m/s-12m/s}{20s-10s}\\\\&=&\frac{0m/s}{10s}\\\\&=&0m/s^2\end{eqnarray}}\)
\(・20s{\le}t{\le}40s\)のとき
\(\displaystyle{\begin{eqnarray}a&=&\frac{0m/s-12m/s}{40s-20s}\\\\&=&\frac{-12m/s}{20s}\\\\&=&-0.6m/s^2\end{eqnarray}}\)
以上から、\(a-t\)グラフは下図の上側のグラフのようになります。
○位置について
位置と速度の関係式は、速度の定義式
\(\displaystyle{\textcolor{green}{v=\frac{x_{あと}-x_{はじめ}}{t_{あと}-t{はじめ}}}}\)
になります。
また、位置はv-tグラフの面積となります。
\(・0s{\le}t{\le}10s\)のとき
この間での時刻を\(t^{\prime}\)、時刻\(t^{\prime}\)のときの速度を\(v^{\prime}\)とし、これをあとの状態とします。
はじめ:t=0sでv=0m/s
あと:\(t=t^{\prime} (0s{\le}t{\le}10s)\)で\(v=v^{\prime}\)
また、この間での加速度は\(+1.2m/s^2\)なので
\(\displaystyle{\begin{eqnarray}&&+1.2m/s^2=\frac{v^{\prime}[m/s]-0m/s}{t^{\prime}[s]-0s}\\\\{\Leftrightarrow}&&v^{\prime}[m/s]=1.2t^{\prime}\end{eqnarray}}\)
また、v-tグラフの面積から、
\(\displaystyle{\begin{eqnarray}x[m]&=&\frac{1}{2}v^{\prime}t^{\prime}\\\\&=&\frac{1}{2}×(1.2t^{\prime})×t^{\prime}\\\\&=&0.6{t^{\prime}}^2\end{eqnarray}}\)
これは、原点を頂点とする下に凸の2次関数のグラフとなります。
(x-y座標における\(y=0.6x^2\)のグラフと同じ)
\(t^{\prime}=10s\)のとき
\(\displaystyle{\begin{eqnarray}x[m]&=&0.6(t^{\prime})^2\\\\&=&0.6×10^2\\\\&=&60m\end{eqnarray}}\)
\(・10s{\le}t{\le}20s\)のとき
この間での時刻を\(t^{\prime}\)、時刻\(t^{\prime}\)のときの速度を\(v^{\prime}\)とし、これをあとの状態とします。
はじめ:t=10sでv=+12m/s
あと:\(t=t^{\prime} (10s{\le}t{\le}20s)\)で\(v=v^{\prime}\)
また、この間での加速度は\(0m/s^2\)なので
\(\displaystyle{\begin{eqnarray}&&0m/s^2=\frac{v^{\prime}[m/s]-12m/s}{t^{\prime}[s]-0s}\\\\{\Leftrightarrow}&&v^{\prime}[m/s]=12m/s\end{eqnarray}}\)
位置は\(0s{\le}t{\le}10s\)までの面積に\(10s{\le}t{\le}t^{\prime}\)までの面積を足したものなので
\(\displaystyle{\begin{eqnarray}x[m]&=&60m+12(t^{\prime}-10)\\\\&=&12t^{\prime}-60\end{eqnarray}}\)
これは、切片が-60で傾きが12の直線の\(10s{\le}t{\le}20s\)の範囲となります。
(x-y座標における\(y=12x-60\)のグラフと同じ)
また、\(t^{\prime}=10s\)のとき
\(\displaystyle{\begin{eqnarray}x[m]&=&12t^{\prime}-60\\\\&=&12×10-60\\\\&=&60m\end{eqnarray}}\)
\(t^{\prime}=20s\)のとき
\(\displaystyle{\begin{eqnarray}x[m]&=&12t^{\prime}-60\\\\&=&12×20-60\\\\&=&180m\end{eqnarray}}\)
\(・20s{\le}t{\le}40s\)のとき
この間での時刻をt、時刻tのときの速度をvとし、これをあとの状態とします。
はじめ:t=20sでv=+12m/s
あと:\(t=t^{\prime} (0s{\le}t{\le}10s)\)で\(v=v^{\prime}\)
また、この間での加速度は\(-0.6m/s^2\)なので
\(\displaystyle{\begin{eqnarray}&&-0.6m/s^2=\frac{v^{\prime}[m/s]-12m/s}{t^{\prime}[s]-20s}\\\\{\Leftrightarrow}&&-0.6(t^{\prime}-20)=v^{\prime}-12\\\\{\Leftrightarrow}&&-0.6t^{\prime}+12=v^{\prime}-12\\\\{\Leftrightarrow}&&v^{\prime}=-0.6t^{\prime}+24\end{eqnarray}}\)
また、位置は\(0s{\le}t{\le}20s\)までの面積に\(20s{\le}t{\le}t^{\prime}\)までの面積を足したものなので
\(\displaystyle{\begin{eqnarray}x[m]&=&180m+\frac{1}{2}(12+v^{\prime})(t^{\prime}-20)\\\\&=&180m+\frac{1}{2}\left\{12+(-0.6t^{\prime}+24)\right\}(t^{\prime}-20)\\\\&=&180m+\frac{1}{2}(-0.6t^{\prime}+36)(t^{\prime}-20)\\\\&=&180m+\frac{1}{2}\left\{-0.6(t^{\prime})^2+12t^{\prime}+36t^{\prime}-720\right\}\\\\&=&180-0.3{t^{\prime}}^2+24t^{\prime}-360\\\\&=&-0.3{t^{\prime}}^2+24t^{\prime}-180\end{eqnarray}}\)
これを平方完成すると
\(\displaystyle{\begin{eqnarray}x&=&-0.3{t^{\prime}}^2+24t^{\prime}-180\\\\&=&-0.3({t^{\prime}}^2-80t^{\prime})-180\\\\&=&-0.3(t-40)^2+480-180\\\\&=&-0.3(t-40)^2+300\end{eqnarray}}\)
これは、頂点がt=40、x=300である下に凸の2次関数のグラフの\(20s{\le}t{\le}40s\)の範囲となります。
(x-y座標における\(y=-0.3(x-40)^2+300\)のグラフと同じ)
\(t^{\prime}=20s\)のとき
\(\displaystyle{\begin{eqnarray}x[m]&=&-0.3(t-40)^2+300\\\\&=&-0.3(20-40)^2+300\\\\&=&-0.3×400+300\\\\&=&-120+300\\\\&=&180m\end{eqnarray}}\)
\(t^{\prime}=40s\)のとき
\(\displaystyle{\begin{eqnarray}x[m]&=&-0.3(t-40)^2+300\\\\&=&-0.3(40-40)^2+300\\\\&=&0+300\\\\&=&300m\end{eqnarray}}\)
以上から、
\(0s{\le}t{\le}10s\)のとき
\(\displaystyle{x=0.6{t^{\prime}}^2}\)
\(10s{\le}t{\le}20s\)のとき
\(\displaystyle{x=12t^{\prime}-60}\)
\(20s{\le}t{\le}40s\)のとき
\(\displaystyle{x=-0.3(t^{\prime}-40)^2+300}\)
よって、x-tグラフの概形は下図の下側のグラフのようになります。
※
x-tグラフを求める際に、この位置xを表す関数を点Oを原点として求めましたが、次のように原点をずらしていき求めた方が計算が楽になります。
\(○0s{\le}t{\le}10s\)のとき
原点Oを基準として
\(v^{\prime}=1.2t^{\prime}\)
\(x=0.6{t^{\prime}}^2\)
これは、原点を頂点とする下に凸の2次関数のグラフの\(0s{\le}t{\le}10s\)部分。
また、\(t^{\prime}=10\)のとき
\(\displaystyle{\begin{eqnarray}x&=&0.6{t^{\prime}}^2\\\\&=&0.6×10^2\\\\&=&60\end{eqnarray}}\)
\(○10s{\le}t{\le}20s\)のとき
\(t=10s\)のときを基準とします。
x-tグラフにおいては、点(10,60)が基準となります。
このとき、
\(v^{\prime}=12\)
位置は、すでに60m進んだところを基準と考えるので、この部分から何m進むかを考えるとv-tグラフの面積から
\(\displaystyle{\begin{eqnarray}x&=&12t^{\prime}\end{eqnarray}}\)
上記の式
\(\displaystyle{\begin{eqnarray}x&=&12t^{\prime}\end{eqnarray}}\)
は傾き12の直線を表します。
また、t=20sのとき、上式においては10sから10s後のことなので\(t^{\prime}=10s\)として
\(\displaystyle{\begin{eqnarray}x&=&12t^{\prime}\\\\&=&12×10\\\\&=&120\end{eqnarray}}\)
よって、x-tグラフにおいては点(10,60)を基準としてt軸方向に+10、x軸方向に+120進んだ点と点(10,60)を結ぶ直線となります。
\(○20s{\le}t{\le}40s\)のとき
\(t=20s\)のときを基準とします。
x-tグラフにおいては、点(20,180)が基準となります。
このとき、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-0.6m/s^2=\frac{v^{\prime}-12m/s}{t^{\prime}-0s}\\\\{\Leftrightarrow}&&v^{\prime}=-0.6t^{\prime}+12\end{eqnarray}}\)
位置は、すでに180m進んだところを基準と考えるので、この部分から何m進むかを考えるとv-tグラフの面積から
\(\displaystyle{\begin{eqnarray}x&=&\frac{1}{2}(12t^{\prime}+v^{\prime})t^{\prime}\\\\&=&\frac{1}{2}\left\{12+(-0.6t^{\prime}+12)\right\}t^{\prime}\\\\&=&\frac{1}{2}(-0.6t^{\prime}+24)t^{\prime}\\\\&=&-0.3{t^{\prime}}^2+12\end{eqnarray}}\)
平方完成して
\(\displaystyle{\begin{eqnarray}x&=&-0.3{t^{\prime}}^2+12\\\\&=&-0.3({t^{\prime}}^2-40t^{\prime})\\\\&=&-0.3(t^{\prime}-20)^2+120\end{eqnarray}}\)
現在点(20,180)を基準としているので、この点からt軸方向に+20、x軸方向に+120進んだ点を頂点とする上に凸の2次関数のグラフとなります。
また、t=20sのとき、上式においては\(t^{\prime}=0s\)のときなので
\(\displaystyle{\begin{eqnarray}x&=&-0.3(t^{\prime}-20)^2+120\\\\&=&-0.3(0-20)^2+120\\\\&=&-0.3×400+120\\\\&=&0\end{eqnarray}}\)
これは、基準点(20,180)を通ることを意味しています。
t=40sのとき、上式においては\(t^{\prime}=20s\)のときなので
\(\displaystyle{\begin{eqnarray}x&=&-0.3(t^{\prime}-20)^2+120\\\\&=&-0.3(20-20)^2+120\\\\&=&0+120\\\\&=&120\end{eqnarray}}\)
以上から、このグラフは点(20,180)を通り、この点からt軸方向に+20、x軸方向に+120進んだ点を頂点とする上に凸の2次関数となります。
基準点を変更させて考えるときは、\(v-t\)グラフの基準点と\(x-t\)グラフや\(a-t\)グラフにおける基準点との関係性に十分注意するようにしましょう。
式が簡単になる分、基準点の捉え方の部分でミスをする可能性があります。
4.平均の加速度
\(\underline{\bf{[問題]}}\)
同一直線上を左右方向に走っている人について、4.0s間で
i)右向きに2.0m/sから右向きに6.0m/s
ii)右向きに2.0m/sから左向きに4.0m/s
にそれぞれ変化した場合の平均の加速度を求め、v-tグラフを描け。
※
この問題は、変位・速度・加速度の練習問題でも扱っています。
→変位・速度・加速度(補足解説と練習問題)
\(\underline{\bf{[解答]}}\)
この問題は「変位・速度・加速度」の練習問題でも扱いましたが、こちらではv-tグラフに注目してみます。
加速度の定義式は
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\vec{a}=\frac{{\bf{(あとの速度)}}-{\bf{(はじめの速度)}}}{{\bf{(あとの時間)}}-{\bf{(はじめの時間)}}}\end{eqnarray}}}\)
また、右向きを正とします。
i)
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=+6.0m/s
から、加速度の定義式より
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(+6.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{+4.0m/s}{4.0s}\\\\&=&+1.0m/s^2\end{eqnarray}}\)
求めた加速度はv-tグラフの傾きとなるので、v-tグラフは下図のようになります。
ii)
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=-4.0m/s
から、加速度の定義式より
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(-4.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{-6.0m/s}{4.0s}\\\\&=&-1.5m/s^2\end{eqnarray}}\)
求めた加速度はv-tグラフの傾きとなるので、v-tグラフは下図のようになります。
5.等加速度直線運動とv-tグラフの利用
5-1.問題1
\(\underline{\bf{[問題1]}}\)
速さ30m/sで右向きに運動していた物体が、等加速度直線運動をして6.0秒後に左向きの速さ15m/sになったとき、
1)加速度の大きさと向き
2)物体の速度が0となるのは、はじめの時刻から何秒後か
3)物体の速度が0となるのは、はじめの位置からどちら向きに何mのところか
を求めよ。
\(\underline{\bf{[解答1]}}\)
はじめ、物体は右向きに運動しているので、右向きを正とします。
状況を整理すると、
はじめ:t=0sで右向きの速さ30m/s
→t=0のとき、+30m/s(右向き正なので)
あと:t=6sで左向きの速さ15m/s
→t=6sのとき、-15m/s(右向き正なので)
また、
\(\textcolor{green}{\bf{等加速度直線運動}}\)
→\(\textcolor{green}{\bf{v-tグラフが直線}}\)
これより、v-tグラフの概形は下図のようになります。
1)
加速度の定義式から
\(\displaystyle{\begin{eqnarray}a&=&\frac{-15m/s-(+30m/s)}{6.0s-0s}\\\\&=&\frac{-45m/s}{6.0s}\\\\&=&-7.5m/s^2\end{eqnarray}}\)
右向き正なので、求める加速度は
\(\underline{{\bf{左向きに}}7.5m/s^2}\)
2)
求める時間は、v-tグラフ中の\(\textcolor{blue}{t^{\prime}}\)です。
この点をあとの状態と考えると
はじめ:t=0で+30m/s
あと:\(t=t^{\prime}\)で0m/s
これより、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-7.5m/s^2=\frac{0m/s-(+30m/s)}{t^{\prime}-0s}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{-30m/s}{-7.5m/s^2}\\\\{\Leftrightarrow}&&t^{\prime}=4.0s\end{eqnarray}}\)
よって
\(\underline{\bf{4.0秒後}}\)
3)
求める変位は、v-tグラフ中の斜線部面積\(\textcolor{blue}{x}\)なので、三角形の面積を求めて
\(\displaystyle{\begin{eqnarray}x&=&\frac{1}{2}×30m/s×t^{\prime}\\\\&=&\frac{1}{2}×30m/s×4.0s\\\\&=&+60m\end{eqnarray}}\)
右向き正なので、求める変位は
\(\underline{{\bf{右向きに}}60m}\)
5-2.問題2
\(\underline{\bf{[問題2]}}\)
東向きに32km/hで走っていたバイクが、ブレーキをかけたところ、等加速度直線運動をして20m進んでから止まった。
このときの、加速度と止まるまでの時間を求めよ。
\(\underline{\bf{[解答2]}}\)
はじめ、東向きに運動しているので東向きを正とします。
ここで、32km/hの単位をm/sになおしておきます。
※単位についてはこちら
→単位の計算や換算(変換)方法
\(\displaystyle{\begin{eqnarray}32km/h&=&\frac{32\textcolor{green}{k}m}{\textcolor{green}{h}}\\\\&=&\frac{32×\textcolor{green}{10^3}m}{\textcolor{green}{3600s}}\\\\&=&10m/s\end{eqnarray}}\)
次に、状況を整理していきます。
はじめ:t=0sのとき、東向きに32km/h
→t=0sのとき+10m/s(東向き正なので)
あと:\(t=t_{あと}\)のとき、止まった
→\(t=t_{あと}\)のとき、0m/s
20m進んで
→v-tグラフの面積が20m
等加速度直線運動をして
→v-tグラフが直線
以上のことからv-tグラフを描くと下図のようになります。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}a&=&\frac{0m/s-(+10m/s)}{t_{あと}-0s}\\\\&=&\frac{-10m/s}{t_{あと}} \cdots①\end{eqnarray}}\)
v-tグラフの面積から
\(\displaystyle{\begin{eqnarray}&&20m=\frac{1}{2}×10m/s×t_{あと}\\\\{\Leftrightarrow}&&t_{あと}=4.0s \cdots②\end{eqnarray}}\)
\(t_{あと}=4.0s\)が分かったので、②を①に代入して、
\(\displaystyle{\begin{eqnarray}a&=&\frac{-10m/s}{t_{あと}}\\\\&=&\frac{-10m/s}{4.0s}\\\\&=&-2.5m/s^2\end{eqnarray}}\)
以上から、東向きを正としているので
加速度
\(\underline{{\bf{西向きに}}2.5m/s^2}\)
時間
\(\underline{\bf{4.0秒}}\)
6.記録タイマー
\(\underline{\bf{[問題]}}\)
等加速度直線運動をする物体の運動を、打点間隔\(\displaystyle{\frac{1}{10}}\)秒の打点タイマーで測定したところ下図のようになった。
図中の最初の打点Oにおける時刻を0としたとき、v-tグラフを描き、この物体の加速度の大きさを求めよ。
\(\underline{\bf{[解答]}}\)
「時刻t[s]」と「位置x[cm]」と「0.1sごとの移動距離[cm]」と「平均の速さ[m/s]」の表を作成します。
時刻は打点間隔が\(\displaystyle{\frac{1}{10}}\)秒、すなわち0.1sなので、O→Aまでで0.1sかかり、A→Bまでで0.1sかかり…となります。
いま、打点Oを時刻0とするので、例えば物体が打点Bだけ進んだ位置では時刻0.2sとなります。
0.1sごとの移動距離は、例えばO→Aまで進むのに0.1sかかっているので、この間での移動距離は
\(4.0cm-0cm=4.0cm\)
となります。
A→Bまででも、0.1sかかっているのでこの間での移動距離は
\(9.9cm-4.0cm=5.9cm\)
となります。
平均の速さは、例えばO→Aを考えると、0.1sで4.0cm進んでいるので平均の速さは
\(\displaystyle{\begin{eqnarray}\frac{4.0cm}{0.1s}&=&\frac{4.0×10^{-2}m}{0.1s}\\\\&=&0.40m/s\end{eqnarray}}\)
A→Bでは、先ほど求めたように0.1sで5.9m進んでいるので、平均の速さは
\(\displaystyle{\begin{eqnarray}\frac{5.9cm}{0.1s}&=&\frac{5.9×10^{-2}m}{0.1s}\\\\&=&0.59m/s\end{eqnarray}}\)
となります。
このように、各区間について各項目を求めていき、表を作成すると以下のようになります。
この表において、もとめた速さは平均の速さなので、v-tグラフにおいては、各区間の平均の速さは、中央時刻における瞬間の速さとみなします。
※
各区間は0.1s間なので、各区間における平均の速さは、この区間における0.05s時の速さとみなす。
これをふまえてv-tグラフを描くと、下図のようになります。
また、加速度の大きさはこのv-tグラフの傾きの大きさとなるので、t=0.05sの点とt=0.55sの点を考えて、加速度の定義式から
\(\displaystyle{\begin{eqnarray}a&=&\frac{1.35m/s-0.40m/s}{0.55s-0.05s}\\\\&=&\frac{0.95m/s}{0.50s}\\\\&=&1.9m/s^2\end{eqnarray}}\)
よって、加速度の大きさは
\(\underline{1.9m/s^2}\)
※
各区間の加速度を計算してみると、どの区間においても\(1.9m/s^2\)となり、v-tグラフは直線になることがわかります。
問題文に、物体は等加速度直線運動をすると記載されているので、v-tグラフが直線になることはわかりますが、各区間の加速度を計算することによってもグラフが直線となることを確認することができます。
7.v-tグラフにおける変位と移動距離
\(\underline{\bf{[問題]}}\)
直線上を運動する物体が、右向きの速さ20m/sで点Oを通過した8.0秒後に左向きの速さ12m/sになった。
物体は等加速度直線運動をするものとして、点Oを原点とした際の8.0秒後の物体の位置と移動距離を求めよ。
\(\underline{\bf{[解答]}}\)
はじめ物体は右向きに移動しているので、右向きを正とします。
状況を整理すると
はじめ:t=0sで右向きの速さ20m/s
→t=0sで+20m/s(右向き正なので符合は正)
あと:t=8.0sで左向きの速さ12m/s
→t=8.0sで-12m/s(右向き正なので符合は負)
物体は等加速度直線運動をする
→v-tグラフは直線
以上のことからv-tグラフを描くと下図のようになります。
\(t^{\prime}\)は物体の速度が0となる時刻。
\(\textcolor{red}{S_1}\)は、t軸よりも上の面積なので、正の面積となります。
すなわち、正の方向に動いた距離となります。
\(\textcolor{blue}{S_2}\)は、t軸よりも下の面積なので、負の面積となります。
すなわち、負の方向に動いた距離となります。
問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}a&=&\frac{-12m/s-(+20m/s)}{8.0s-0}\\\\&=&\frac{-32m/s}{8.0s}\\\\&=&-4.0m/s^2\end{eqnarray}}\)
また、物体の速度が0となる点をあとの状態だと考えると、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&-4.0m/s^2=\frac{0m/s-(+20m/s)}{t^{\prime}-0s}\\\\{\Leftrightarrow}&&t^{\prime}=\frac{-20m/s}{-4.0m/s^2}\\\\{\Leftrightarrow}&&t^{\prime}=5.0s\end{eqnarray}}\)
これより、正の面積\(\textcolor{red}{S_1}\)は三角形の面積を求める式から
\(\displaystyle{\begin{eqnarray}\textcolor{red}{S_1}&=&\frac{1}{2}×20m/s×t^{\prime}\\\\&=&\frac{1}{2}×20m/s×5.0s\\\\&=&50m\end{eqnarray}}\)
また、負の面積\(\textcolor{blue}{S_2}\)も三角形の面積を求める式から
\(\displaystyle{\begin{eqnarray}\textcolor{blue}{S_2}&=&\frac{1}{2}×12m/s×(8.0s-t^{\prime})\\\\&=&\frac{1}{2}×12m/s×(8.0s-5.0s)\\\\&=&\frac{1}{2}×12m/s×3.0s\\\\&=&18m\end{eqnarray}}\)
面積の大きさは18mですが、負の面積であり、負の方向(左向き)に進んだ距離となることに注意してください。
※
速度-12m/sを用いると、面積は-18mとなる
ここで
位置=変位
なので、変位を求めて
\(\displaystyle{\begin{eqnarray}{\bf{変位}}&=&\textcolor{red}{S_1}+\textcolor{blue}{S_2}\\\\&=&\textcolor{red}{+50m}+\textcolor{blue}{(-18m)}\\\\&=&+32m\end{eqnarray}}\)
右向き正なので、位置は右向きに32mとなります。
また、移動距離は
\(\displaystyle{\begin{eqnarray}{\bf{移動距離}}&=&\textcolor{red}{S_1}+\textcolor{blue}{|S_2|}\\\\&=&\textcolor{red}{+50m}+\textcolor{blue}{|-18m|}\\\\&=&\textcolor{red}{+50m}+\textcolor{blue}{(+18m)}\\\\&=&+68m\end{eqnarray}}\)
以上から
位置
\(\underline{{\bf{右向きに}}32m}\)
移動距離
\(\underline{68m}\)
となります。
はてなブログ内関連記事
1-1.変位・速度・加速度(補足解説と練習問題)
変位・速度・加速度の記事で解説した内容の補足解説と練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、変位・速度・加速度の記事で解説していなかった補足内容があれば、この記事に載せています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.単位の変換と平均の速さ
\(\underline{\bf{<目的>}}\)
・単位の扱いに慣れる
単位についてはこちらも参考にしてください
→単位の計算や換算(変換)方法
\(\bf{\underline{[問題]}}\)
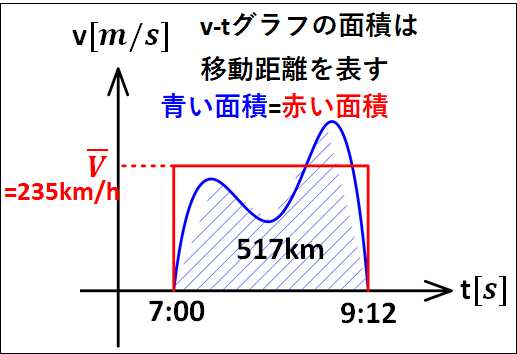
新幹線が駅間距離517kmある京都駅から東京駅を移動することを考える。
京都駅を7:00に出発し、東京駅に9:12に到着するとするとき、この京都駅-東京駅間における新幹線の平均の速さはいくらになるか?
単位をkm/hとm/sで答えよ。
\(\underline{\bf{[解答]}}\)
km/hのhは、1時間という意味です。
よって、この場合は単位時間(1時間)あたりに平均何km進むかを答えるというものになります。
はじめの状況と、あとの状況をまとめると
はじめ:7:00に京都駅(0km)
あと:9:12に東京駅(517km)
また、9:12の12の単位は分なのでこれも時間になおして表示すると
\(\displaystyle{9\frac{12}{60}}\)
となります。
何km/hかを聞かれているので、距離の単位はkm、時間の単位はh(時)として平均の速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\overline{V}=\frac{x_{あと}-x_{はじめ}}{t_{あと}-t_{はじめ}}\end{eqnarray}}}\)
から
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{517km-0km}{9\frac{12}{60}h-7h}\\\\&=&\frac{517km}{2\frac{12}{60}h}\\\\&=&\frac{517km}{\frac{132}{60}h}\end{eqnarray}}\)
ここで、
\(\textcolor{red}{\bf{方法1}}\)
→分母を先に計算する
先ほどの式から
\(\displaystyle{\begin{eqnarray}\frac{517km}{\frac{132}{60}h}&=&\frac{517km}{2.2h}\\\\&=&235km/h\end{eqnarray}}\)
より、
\(\underline{235km/h}\)(有効数字3桁)
となります。
※有効数字についてはこちら
→有効数字
\(\textcolor{red}{\bf{方法1}}\)
→分子分母に60を掛ける
同様にして、計算途中の式から、
\(\displaystyle{\begin{eqnarray}\frac{517km}{\frac{132}{60}h}&=&\frac{517km×60}{\frac{132}{60}h×60}\\\\&=&\frac{517×60km}{132h}\\\\&=&235km/h\end{eqnarray}}\)
より、
\(\underline{235km/h}\)(有効数字3桁)
となります。
次に、分速m/sを求めていきます。
こちらも、単位の換算については「単位の計算や換算(変換)方法」で扱っているので、目を通してみてください。
\(\displaystyle{\textcolor{green}{\begin{eqnarray}k&=&1000\\\\&=&10^3\end{eqnarray}}}\)
\(\displaystyle{\textcolor{green}{\begin{eqnarray}h&=&3600s\end{eqnarray}}}\)
なので、先ほどの平均の速度の式から、
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{517\textcolor{green}{k}m}{2\frac{12}{60}\textcolor{green}{h}}\\\\&=&\frac{517×\textcolor{green}{10^3}m}{\frac{132}{60}×\textcolor{green}{3600s}}\\\\&=&\frac{517×10^3m}{132×60s}\\\\&=&65.2777{\cdots}m/s\end{eqnarray}}\)
より、
\(\underline{65.3m/s}\)(有効数字3桁)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・小中の復習→単位計算をしっかりする
・計算結果を有効数字でかえす
ちなみに、京都駅から東京駅までの間、新幹線の速さは常に一定ではありません。
途中途中で速くなったり、遅くなったりしています。
新幹線だと想像しにくいかもしれませんが、自動車だとスピードのメーターが常に一定の値を指していることはなく、また信号でとまった際などには速さは0となります。
出発するときも、いきなり60km/hがでているわけではなく、0km/hから徐々に速さが大きくなっていき60km/hに至ります。
平均の速さというのは、上記のように瞬間瞬間での速さではなく、ある地点からある地点までもしも一定の速さで進んだらどれだけの速さになるか?という値になります。
別記事で解説しているv-tグラフを用いると、京都駅から東京駅までの瞬間瞬間の速さはばらばらですが、同じv-tグラフの面積になるように平らにしたものが平均の速度となります。
※v-tグラフについてはこちら
→v-tグラフと等加速度直線運動
2.平均の速さと瞬間の速さ
\(\underline{\bf{[問題]}}\)
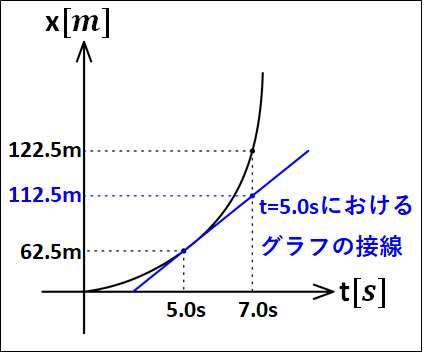
次のx-tグラフにおける、時刻5.0sから7.0sまでの平均の速さと、時刻5.0sにおける瞬間の速さを求めよ。
※x-tグラフは時間と位置の関係を表したグラフ。
y-tグラフやs-tグラフということもある
\(\underline{\bf{[解答]}}\)
○平均の速さ
はじめとあとの点を考えると、以下のようになります。
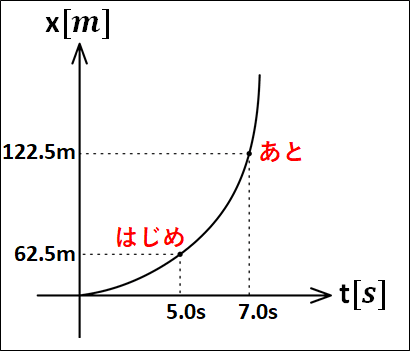
こちらも、はじめとあとの状況をまとめると
はじめ:5.0sで62.5m
あと:7.0sで122.5m
よって、平均の速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\overline{V}=\frac{x_{あと}-x_{はじめ}}{t_{あと}-t_{はじめ}}\end{eqnarray}}}\)
から、
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{122.5m-62.5m}{7.0s-5.0s}\\\\&=&\frac{60.0m}{2.0s}\\\\&=&30m/s\end{eqnarray}}\)
よって、平均の速さについては、
\(\underline{30m/s}\)(有効数字2桁)
となります。

\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・x-t(y-t,s-t)グラフの意味
・有効数字
○瞬間の速さ
時刻5.0sにおける瞬間の速さは、この時刻における接線の傾きとなります。
瞬間の速さを考えるために、時刻5.0sの点からほんの少しだけの時間\(\Delta{t}\)経った点を考えます。
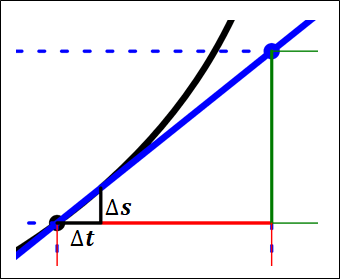
このときの時刻は、(5.0s+\(\Delta{t})\)となります。
またこの時の物体の位置を\(\Delta{s}\)とすると、位置\(x[m]\)は(62.5m+\(\Delta{s})\)となります。
これより、時刻5.0sを"はじめ"、ほんの少しの時間\(\Delta{t}\)だけ経ったあとの状態を"あと"とすると、
はじめ:5.0sのとき62.5m
あと:5.0s+\(\Delta{t}\)のとき62.5m+\(\Delta{s}\)
となります。
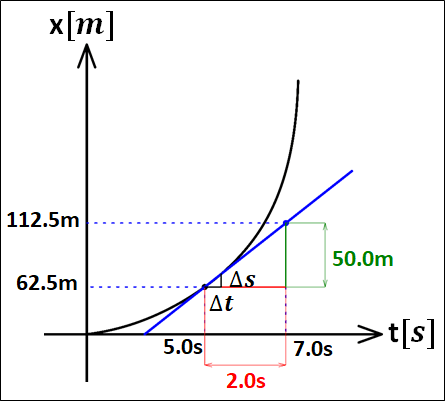
このときの速さを考えると、定義式から
\(\displaystyle{\begin{eqnarray}V&=&\frac{(62.5+\Delta{s})-62.5m}{(5.0s+\Delta{t})-5.0s}\\\\&=&\frac{\Delta{s}}{\Delta{t}}\end{eqnarray}}\)
これは、接線の傾きを表します。
また、グラフから下図の直角三角形が相似であることがわかります。
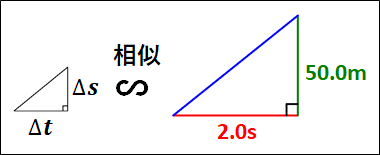
上図2つの直角三角形は相似なので、斜辺の傾きは同じとなります。
よって、
\(\displaystyle{\begin{eqnarray}V&=&\frac{\Delta{s}}{\Delta{t}}\\\\&=&\frac{50.0m}{2.0s}\\\\&=&25m/s\end{eqnarray}}\)
以上から、時刻5.0sにおける瞬間の速さは
\(\underline{25m/s}\)(有効数字2桁)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・微小量の扱い方
→ほんの少しだけの変化を考える
(数学でいう微分係数)
※微分係数についてはこちらも参考にしてください
→微分係数と導関数
3.変位と移動距離と平均の速度
\(\underline{\bf{[問題]}}\)
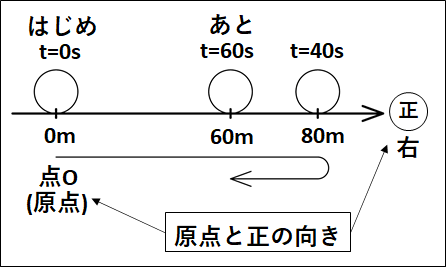
ある物体が点Oから同一直線上を右に向かって40秒間で80m移動した後、左に向かって20秒間で20m移動した。
点Oを出発してから60秒間での、この物体の「変位・移動距離・平均の速度」を求めよ。
\(\underline{\bf{[解答]}}\)
問題文中に「平均の\(\textcolor{red}{\bf{速度}}\)」を求めよとあります。
速度とは「\(\textcolor{red}{\bf{ベクトル}}\)」(向きと大きさがある)なので、以下の設定をする必要があります。
\(\textcolor{red}{\bf{・軸の設定}}\)
\(\textcolor{red}{\bf{・原点と正の向きの設定}}\)
今回は、点Oを出発してからの話なので「原点」を点O、はじめ右向きに移動するので右向きを正としておきます。
図示すると下図のようになります。
○変位
変位の定義式
\(\displaystyle{\textcolor{green}{\overrightarrow{x}={\bf{(あとの座標)-(はじめの座標)}}}}\)
から、
\(\displaystyle{\begin{eqnarray}\overrightarrow{x}&=&(60m)-(0m)\\\\&=&+60m\end{eqnarray}}\)
軸は右向きを正としているので、変位の符合(+)は翻訳すると右向きという意味になります。
よって変位は
\(\underline{{\bf{右向きに}}60m}\)
となります。
○移動距離
移動した距離は、右向きに80m移動した後、左向きに20m移動しているので
\(80m+20m=100m\)
よって移動距離は
\(\underline{100m}\)
となります。
○平均の速度
これまでと同様に、平均の速度\(\vec{V}\)の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\vec{V}=\frac{{\bf{(あとの座標)}}-{\bf{(はじめの座標)}}}{{\bf{(あとの時間)}}-{\bf{(はじめの時間)}}}\end{eqnarray}}}\)
から、
\(\displaystyle{\begin{eqnarray}\vec{V}&=&\frac{60m-0m}{60s-0s}\\\\&=&\frac{+60m}{60s}\\\\&=&+1.0m/s\end{eqnarray}}\)
こちらも変位と同様に、右向きを正としているので速度の符合は翻訳すると右向きであることを意味しています。
よって平均の速度は
\(\underline{{\bf{右向きに}}1.0m/s}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・ベクトルの処理の仕方
→図と数式で扱う
4.平均の加速度
同一直線上を左右に走っている人について、4.0s間で
i) 右向きに2.0m/sから右向きに6.0m/s
ii) 右向きに2.0m/sから左向きに4.0m/s
にそれぞれ変化した場合の平均の加速度を求めよ。
※
この問題は、v-tグラフの練習問題でも扱います。
\(\underline{\bf{[解答]}}\)
加速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\vec{a}=\frac{\bf{(あとの速度)-(はじめの速度)}}{\bf{(あとの時間)-(はじめの時間)}}\end{eqnarray}}}\)
を用います。
また、加速度もベクトルなので軸を設定する必要があるので、右向きを正としておきます。
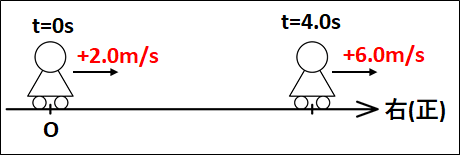
i)
図示すると下図のようになります。
はじめとあとの時間と速度をまとめてみます。
右向きを正としているので
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=+6.0m/s
これと、加速度の定義式から
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(+6.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{+4.0m/s}{4.0s}\\\\&=&+1.0m/s^2\end{eqnarray}}\)
右向きを正としているので加速度の符合は翻訳すると右向きであることを意味しています。
よって平均の加速度は
\(\underline{{\bf{右向きに}}1.0m/s^2}\)
となります。
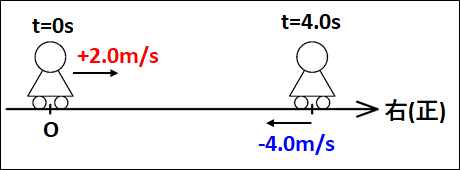
ii)
図示すると下図のようになります。
はじめとあとの時間と速度をまとめてみます。
右向きを正としているので
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=-4.0m/s
これと、加速度の定義式から
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(-4.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{-6.0m/s}{4.0s}\\\\&=&-1.5m/s^2\end{eqnarray}}\)
右向きを正としているので加速度の符合は翻訳すると左向きであることを意味しています。
よって平均の加速度は
\(\underline{{\bf{左向きに}}1.5m/s^2}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・速度・加速度の扱い
→ベクトル
→向きと大きさがある
→1.軸の設定
2.原点と正の方向の設定
・加速度の定義
5.変位と速度
\(\underline{\bf{[問題]}}\)
x-y平面上を等速直線運動をしている物体が、点A(4.0m,11m)から点B(12m,2.0m)に3.0sで移動したときの変位と速度の成分(x成分とy成分)を求めよ。
\(\underline{\bf{[解答]}}\)
○変位
変位はベクトルとなるので、図示すると下図のようになります。
※ベクトルについてはこちら
→ベクトルの演算と成分表示
→力とベクトル
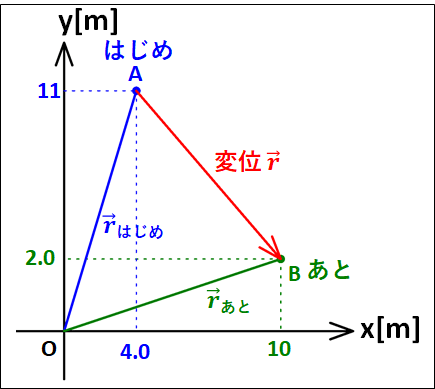
図中の\(\textcolor{blue}{\vec{r}_{はじめ}}\)と\(\textcolor{green}{\vec{r}_{あと}}\)を"位置ベクトル"といいます。
この位置ベクトルを用いると、変位ベクトル\(\textcolor{red}{\vec{r}}\)は
\(\displaystyle{\textcolor{red}{\vec{r}}=\textcolor{green}{\vec{r}_{あと}}-\textcolor{blue}{\vec{r}_{はじめ}}}\)
のように、
(あとの位置ベクトル)-(はじめの位置ベクトル)
で表すことができます。
それぞれの位置ベクトルを成分表示すると、
\(\displaystyle{\textcolor{blue}{\vec{r}_{はじめ}=\left(\begin{array}{l}4.0m\\11m\end{array}\right)}}\)
\(\displaystyle{\textcolor{green}{\vec{r}_{あと}=\left(\begin{array}{l}10m\\2.0m\end{array}\right)}}\)
これより、変位ベクトル\(\textcolor{red}{\vec{r}}\)は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{r}}&=&\textcolor{green}{\vec{r}_{あと}}-\textcolor{blue}{\vec{r}_{はじめ}}\\\\&=&\textcolor{green}{\left(\begin{array}{l}10m\\2.0m\end{array}\right)}-\textcolor{blue}{\left(\begin{array}{l}4.0m\\11m\end{array}\right)}\\\\&=&\textcolor{red}{\left(\begin{array}{l}10m-4.0m\\2.0m-11m\end{array}\right)}\\\\&=&\textcolor{red}{\left(\begin{array}{r}6.0m\\-9.0m\end{array}\right)}\end{eqnarray}}\)
以上から
変位のx成分
\(\underline{6.0m}\)
変位のy成分
\(\underline{-9.0m}\)
となります。
※
これまでと同様にx成分とy成分を別々で考えると
x軸方向について
はじめのx座標:4.0m
あとのx座標:10m
から、x軸方向の変位は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{x}}&=&\textcolor{green}{10m}-\textcolor{blue}{4.0m}\\\\&=&\textcolor{red}{+6.0m}\end{eqnarray}}\)
同様にしてy軸方向についても考えると
はじめのy座標:11m
あとのy座標:2.0m
から、x軸方向の変位は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{y}}&=&\textcolor{green}{2.0m}-\textcolor{blue}{11m}\\\\&=&\textcolor{red}{-9.0m}\end{eqnarray}}\)
となります。
○速度
速度の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{速度}}\vec{v}&=&\frac{{\bf{変位}}\vec{r}}{\Delta{t}}\\\\\\&=&\frac{\left(\begin{array}{l}6.0m\\-9.0m\end{array}\right)}{3.0s}\\\\\\&=&\left(\begin{array}{l}+2.0m/s\\-3.0m/s\end{array}\right)\end{eqnarray}}\)
以上から
速度のx成分
\(\underline{+2.0m/s}\)
速度のy成分
\(\underline{-3.0m/s}\)
となります。
※
x成分とy成分を別々で考えると
x軸方向について
\(\vec{x}=+6.0m\)
より、x軸方向の速度\(v_x\)は
\(\displaystyle{\begin{eqnarray}v_x&=&\frac{\vec{x}}{\Delta{t}}\\\\&=&\frac{+6.0m}{3.0s}\\\\&=&+2.0m/s\end{eqnarray}}\)
y軸方向について
\(\vec{x}=-9.0m\)
より、y軸方向の速度\(v_y\)は
\(\displaystyle{\begin{eqnarray}v_y&=&\frac{\vec{y}}{\Delta{t}}\\\\&=&\frac{-9.0m}{3.0s}\\\\&=&-3.0m/s\end{eqnarray}}\)
となります。
ちなみに加速度の定義は
\(\displaystyle{{\bf{加速度}}\vec{a}=\frac{{\bf{速度}}\vec{v}}{\Delta{t}}}\)
です。
6.平均の速度
\(\underline{\bf{[問題]}}\)
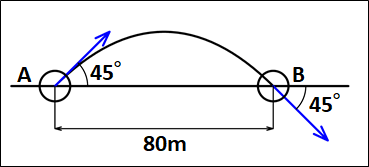
点Aから東方向と45°の角度をなす北向きに物体を転がしたところ、下図のような軌道を描いて、4.0s後に点Aから80m離れた点Bを東方向と45°の角度をなして南向きに通り過ぎた。
このときの、AB間の平均の速度を求めよ。
\(\underline{\bf{[解答]}}\)
変位と速度の定義に忠実にみていきます。
点Aを原点とするx-y座標をとると、点Aと点Bの座標は下図のようになります。
(東向き、北向きを正とする)
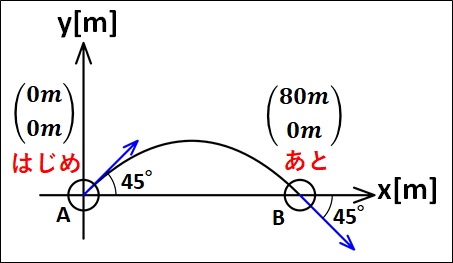
変位\(\vec{r}\)を求めると、これまでと同様に変位の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}\vec{r}&=&\left(\begin{array}{l}80m\\0m\end{array}\right)-\left(\begin{array}{l}0m\\0m\end{array}\right)\\\\&=&\left(\begin{array}{l}80m\\0m\end{array}\right)\end{eqnarray}}\)
変位が求まったので、速度の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{速度}}\vec{v}&=&\frac{{\bf{変位}}\vec{r}}{\Delta{t}}\\\\\\&=&\frac{\left(\begin{array}{l}80m\\0m\end{array}\right)}{4.0s}\\\\\\&=&\left(\begin{array}{l}20m/s\\0m/s\end{array}\right)\end{eqnarray}}\)
以上から、東向きと北向きを正ととっているので、成分をみてみると
\(\underline{{\bf{東向きに}}20m/s^2}\)
\(\underline{{\bf{北向きに}}0m/s^2}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・変位は"あと"と"はじめ"だけで決まる。
途中のルートは関係なし。
はてなブログ内関連記事
2.v-tグラフと等加速度直線運動
\(v-t\)グラフとは、速度\(v\)と時間\(t\)の関係を表したグラフになります。
このグラフには様々な情報が含まれており、問題を解くうえで活用するので、しっかりと理解しておく必要があります。
主に、\(v-t\)グラフの解説や書き方、読み取りの方法を解説しています。
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.v-tグラフ
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{{\bf{・加速度}}a[m/s^2]}\)
\(\textcolor{red}{→v-t{\bf{グラフの傾き}}}\)
\(\textcolor{red}{{\bf{・変位}}x[m]}\)
\(\textcolor{red}{→v-t{\bf{グラフの面積}}}\)
\(v-t\)グラフとは、速度\(v[m/s]\)と時間\(t[s]\)の関係を表したグラフです。
様々な情報が含まれており、問題を解く際に用いるのでしっかりと活用できるようにしなければなりません。
\(v-t\)グラフは基本的にはじめとあとの情報で構成されており、これを図示したものとなります。
例えば、
はじめ:\(t=t_{\bf{はじめ}}(=0)\)のとき\(v=v_{\bf{はじめ}}\)
あと:\(t=t_{\bf{あと}}\)のとき\(v=v_{\bf{あと}}\)
のとき、\(v-t\)グラフは下図のようになります。
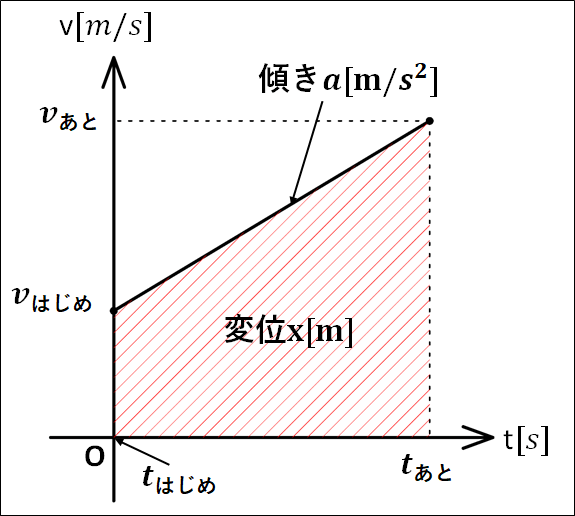
\(\bf{\underline{加速度について}}\)
加速度\(a[m/s^2]\):
→\(v-t\)グラフの傾きを表す
定義式は
\(\displaystyle{a[m/s^2]=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m/s]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}\)
\(a=0\)のとき、\(x\)軸と平行
\(a\gt0\)のとき、右上がり
\(a\lt0\)のとき、右下がり
\(\bf{\underline{変位について}}\)
変位\(x[m]\):
→\(v-t\)グラフの面積
\(v\gt0\)(\(t\)軸より上の面積)のとき正
\(v\lt0\)(\(t\)軸より下の面積)のとき負
変位は、正の面積と負の面積の和になります。
移動距離は、面積の大きさの合計となるので、
\({\bf{(正の面積)}}+|{\bf{(負の面積)}}|\)
で表されます。
\(\underline{v_{\bf{はじめ}}{\bf{について}}}\)
\(v_{\bf{はじめ}}\)を\(\textcolor{red}{\bf{初速度}}\)といい、\(t=0\)のときの速度を意味します。
変位・速度・加速度については、こちらの記事も参考にしてください。
→変位・速度・加速度
\(v-t\)グラフから\(x-t\)グラフを書く際は、変位\(x\)が\(v-t\)グラフの面積であることを利用します。
\(v-t\)グラフから\(a-t\)グラフを書く際は、加速度\(a\)が\(v-t\)グラフの傾きであることを利用します。
これらについては、別記事の練習問題のほうで具体的にみていきたいと思います。
特に、\(v-t\)グラフの傾きが直線(加速度の値が一定)のものを\(\textcolor{red}{\bf{等加速度直線運動}}\)といいます。
※\(v-t\)グラフの面積(変位\(x\)について)
少しの時間を\(dt[s]\)とすると、時間\(dt[s]\)の間の変位は
\(v[m/s]×dt[s]=v dt[m]\)
となります。
(\(m/s×s=m(メートル)\))
グラフでみてみると、
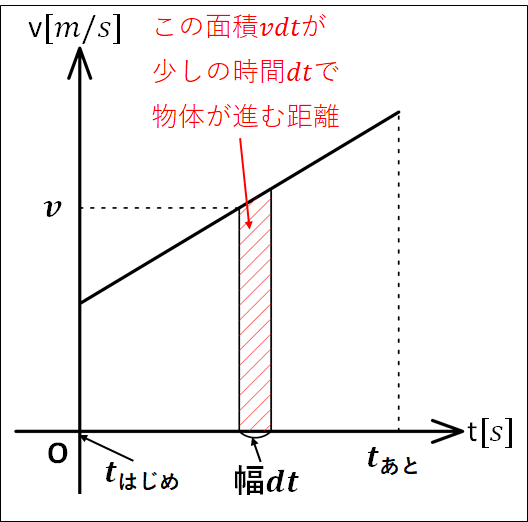
画像では、\(dt\)にはある程度の幅がありますが、実際には限りなく小さい幅であるとイメージしてください。
そうすると、赤色斜線部は画像では台形にみえますが、限りなく細くなっていき線(長方形)であるとみなせます。
なので、一瞬の時間\(dt\)の間の物体の変位は(縦×横)で\(v dt\)となります。
この面積を、\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)まで足していきます。
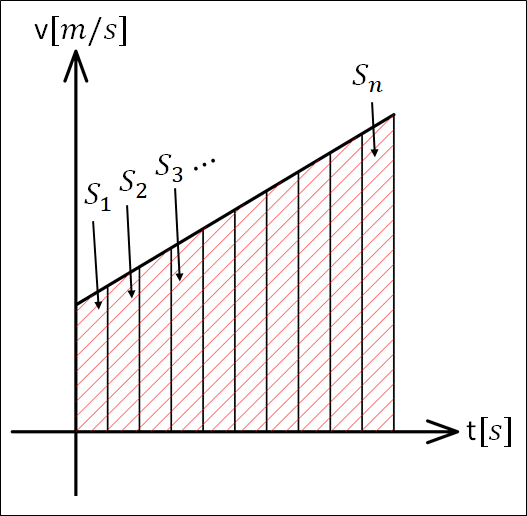
各部分の面積を\(S_{1},S_{2},S_{3}{\cdots}S_{n}\)とすると、\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)までの変位は
\(S_{1}+S_{2}+S{3}+{\cdots}+S_{n}\)
となります。
よって、全体の面積が変位\(x\)となります。
※補足
積分を考える
微小時間\(dt\)の間の変位\(x[m]\)は\(v dt[m]\)。
これを\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)までなめらかに足して(積分して)
\(\displaystyle{x[m]=\int_{t_{\bf{はじめ}}}^{t_{\bf{あと}}}v dt}\)
となります。
グラフと面積については、こちらも参考にしてください
→積分法
→積分法の応用
→よく使う積分の考え方と微積公式まとめ
2.v-tグラフの読み取り
練習問題を通して、\(v-t\)グラフの読み取り練習をします。
使う知識は、
・加速度は\(v-t\)グラフの傾きを表している
・加速度\(a[m/s^2]\)の定義は
\(\displaystyle{a=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}}\)
・\(v-t\)グラフの面積が変位\(x\)を表している
です。
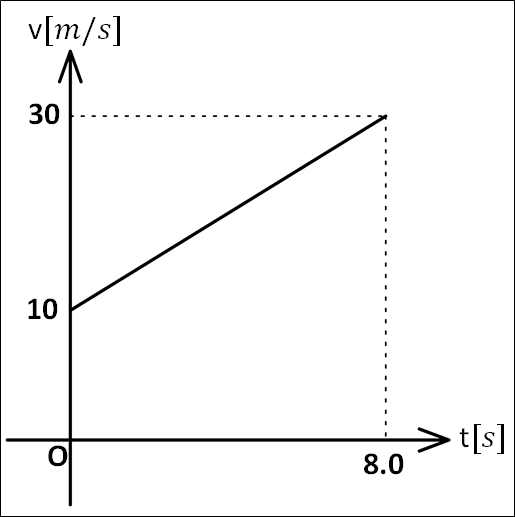
\(\bf{[問題1]}\)
下図の\(v-t\)グラフのように物体が等加速度直線運動をしているとき、
(\(1)\)加速度の正負
(\(2)\)加速度
(\(3)\)時刻\(0\)秒から\(8.0\)秒までの移動距離
を求めよ。
\(\bf{[問題1]の解答}\)
\( (1)\)
グラフは右上がりの直線なので、加速度は正
\( (2)\)
情報をまとめると
はじめ:\(t=0s\)で\(v=10m/s\)
あと:\(t=8.0s\)で\(v=30m/s\)
よって、加速度の定義式から
\(\displaystyle{\begin{eqnarray}a[m/s^2]&=&\frac{30m/s-10m/s}{8.0s-0s}\\\\&=&\frac{20m/s}{8.0s}\\\\&=&+2.5m/s^2\end{eqnarray}}\)
\( (3)\)
グラフから、物体は常に正の方向に進んでいることがわかる。(グラフが常に\(t\)軸より上にあるため)
このことから、移動距離は\(v-t\)グラフの面積となるので、グラフの台形の面積を求めて
\(\displaystyle{\begin{eqnarray}&&(10m/s+30m/s)×8.0s×\frac{1}{2}\\\\=&&160m\\\\=&&1.6×10^2m\end{eqnarray}}\)
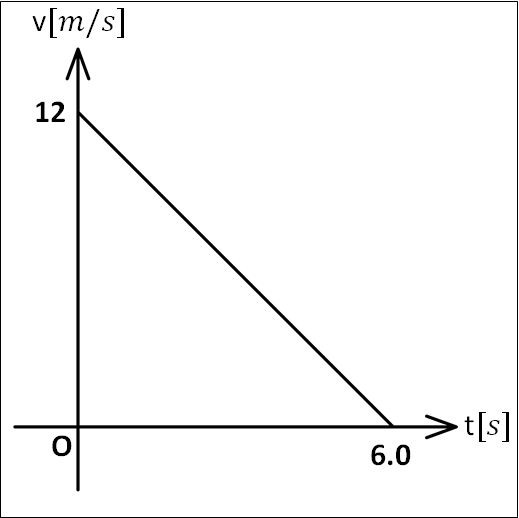
\(\bf{[問題2]}\)
下図の\(v-t\)グラフのように物体が等加速度直線運動をしているとき、
\( (1)\)加速度の正負
\( (2)\)加速度
\( (3)\)時刻(0秒)から\(6.0\)秒までの移動距離
を求めよ。
\(\bf{[問題2]の解答}\)
\( (1)\)
グラフは右下がりの直線なので、加速度は正
\( (2)\)
情報をまとめると
はじめ:\(t=0s\)で\(v=+12m/s\)
あと:\(t=6.0s\)で\(v=0m/s\)
よって、加速度の定義式から
\(\displaystyle{\begin{eqnarray}a[m/s^2]&=&\frac{0m/s-12m/s}{6.0s-0s}\\\\&=&\frac{-12m/s}{6.0s}\\\\&=&-2.0m/s^2\end{eqnarray}}\)
\( (3)\)
グラフから、物体は常に正の方向に進んでいることがわかる。(グラフが常に\(t\)軸より上にあるため)
このことから、移動距離は\(v-t\)グラフの面積となるので、グラフの三角形の面積を求めて
\(\displaystyle{\begin{eqnarray}&&6.0s×12m/s×\frac{1}{2}\\\\=&&36m\end{eqnarray}}\)
3.v-tグラフの作成
与えられた情報から\(v-t\)グラフを作成するには、はじめの情報とあとの情報を把握して、グラフにプロットします。
等加速度直線運動ならば、グラフの傾きが直線(加速度の値が一定)となります。
注意する点としては、わからない部分は自分で文字でおきましょうということぐらいだと思います。
こちらも、練習問題を扱っていきます。
練習問題に使用するのは、加速度の定義式と\(v-t\)グラフの面積を求める式のみです。
\(\bf{[問題1]}\)
物体は等加速度直線運動をするとする。
静止している物体が、右向きの加速度\(1.0m/s^2\)で\(4.0\)秒間移動したとき、この間の変位はどちら向きに何\(m\)か。
\(\bf{[問題1]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理します。
\(\textcolor{red}{\bf{静止している}}\)というのは、速度が\(0m/s\)ということです。
なので、はじめ(\(t=0s\))のとき\(v=0m/s\)という意味になります。
はじめとあとの情報を整理すると
はじめ:
\(t=0s\)で\(v=0m/s\)
あと:
\(t=4.0s\)で\(v=v_{\bf{あと}}[m/s]\)
あとの速度は分からないので、\(v_{\bf{あと}}\)としています。
また、右向きを正としているので、右向きの加速度の符合は\(+\)となります。
右向きの加速度\(1.0m/s^2\)→\(+1.0m/s^2\)
また、加速度は\(v-t\)グラフの傾きを表しています。
今、変位を求めるということなので、変位を\(x[m]\)としておきます。
変位は\(v-t\)グラフの面積となります。
以上のことをふまえて、\(v-t\)グラフを描くと、下図のようになります。
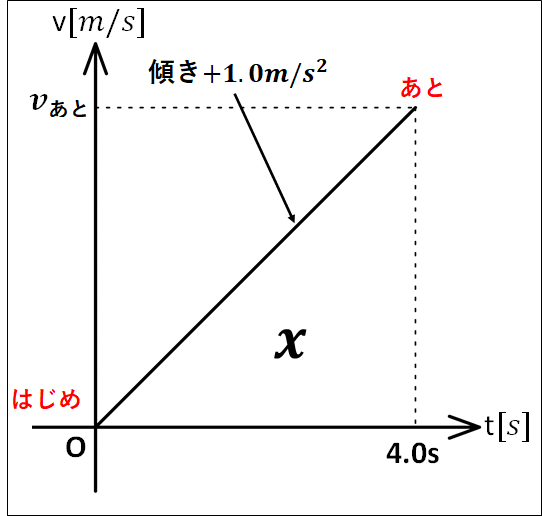
\(v-t\)グラフが描けたところで、問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&1.0m/s^2=\frac{v_{\bf{あと}}-0m/s}{4.0s-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=4.0m/s\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(三角形の面積)から、変位\(x[m]\)は
\(\displaystyle{\begin{eqnarray}x[m]&=&4.0s×v_{\bf{あと}}×\frac{1}{2}\cdots②\end{eqnarray}}\)
\(①\)を\(②\)に代入して
\(\displaystyle{\begin{eqnarray}x[m]&=&4.0s×v_{\bf{あと}}×\frac{1}{2}\\\\&=&4.0s×4.0m/s×\frac{1}{2}\\\\&=&+8.0m\end{eqnarray}}\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}8.0m}\)
となります。
\(\bf{[問題2]}\)
物体は等加速度直線運動をするとする。
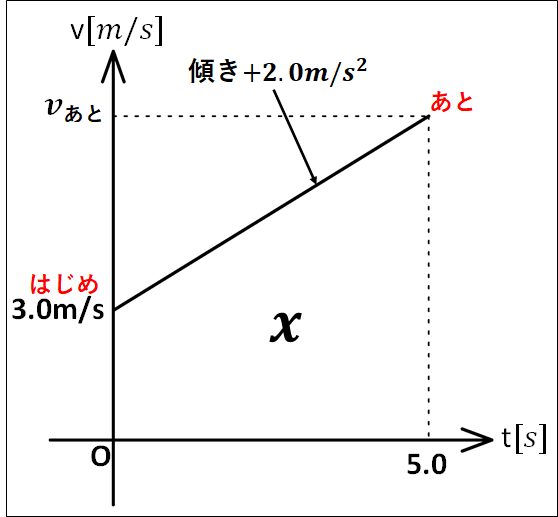
右向きの速さ\(3.0m/s\)で進んでいた物体が、右向きの加速度\(2.0m/s^2\)で\(5.0\)秒間移動したとき、この間の変位はどちら向きに何\(m\)か。
\(\bf{[問題2]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理すると
はじめ:
\(t=0s\)のとき、右向きの速さ\(3.0m/s\)
→\(+3.0m/s\)(右向きを正としているので符合は\(+\))
あと:
\(t=5.0s\)のとき、\(v=v_{\bf{あと}}\)
右向きの加速度\(2.0m/s^2\)
→\(+2.0m/s^2\)(右向きを正としているので符合は\(+\))
これが、\(v-t\)グラフの傾きとなる。
変位\(x[m]\)は\(v-t\)グラフの面積
以上から\(v-t\)グラフを描くと、下図のようになります。
問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&2.0m/s^2=\frac{v_{\bf{あと}}-3.0m/s}{5.0s-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=13m/s\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(台形の面積)から、変位\(x[m]\)は
\(\displaystyle{x[m]=(3.0m/s+v_{\bf{あと}})×5.0s×\frac{1}{2}\cdots②}\)
\(①\)を\(②\)に代入して、
\(\displaystyle{\begin{eqnarray}x[m]&=&(3.0m/s+v_{\bf{あと}})×5.0s×\frac{1}{2}\\\\&=&(3.0m/s+13m/s)×5.0s×\frac{1}{2}\\\\&=&+40m\end{eqnarray}}\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}40m}\)
となります。
\(\bf{[問題3]}\)
物体は等加速度直線運動をするとする。
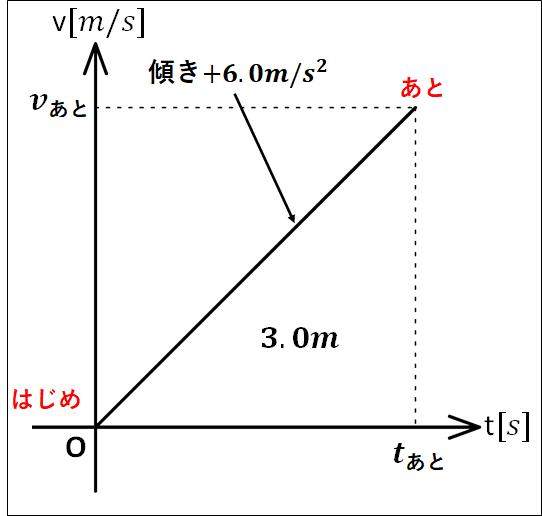
静止していた物体が、右向きの加速度\(6.0m/s^2\)の運動をはじめ、右側に\(3.0m\)移動したとき、物体の速度はどちら向きに何\(m/s\)か。
\(\bf{[問題3]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理すると
はじめ:
\(t=0s\)のとき、静止
→\(0m/s\)
あと:
\(t=t_{\bf{あと}}\)のとき、\(v=v_{\bf{あと}}\)
右向きの加速度\(6.0m/s^2\)
→\(+6.0m/s^2\)(右向きを正としているので符合は\(+\))
これが、\(v-t\)グラフの傾きとなる。
変位\(x[m]\)は\(v-t\)グラフの面積
以上から\(v-t\)グラフを描くと、下図のようになります。
問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&6.0m/s^2=\frac{v_{\bf{あと}}-0m/s}{t_{\bf{あと}}-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=6.0m/s^2×t_{\bf{あと}}\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(三角形の面積)から、変位\(3.0[m]\)は
\(\displaystyle{\begin{eqnarray}&&3.0m=t_{\bf{あと}}×v_{\bf{あと}}×\frac{1}{2}\\\\\Leftrightarrow&&t_{\bf{あと}}=\frac{6m}{v_{\bf{あと}}}\cdots②\end{eqnarray}}\)
\(②\)を\(①\)に代入して、
\(\displaystyle{\begin{eqnarray}&&v_{\bf{あと}}=6.0m/s^2×\frac{6m}{v_{\bf{あと}}}\\\\\Leftrightarrow&&v_{\bf{あと}}^2=6.0^2m^2/s^2\end{eqnarray}}\)
\(v-t\)グラフから、\(v_{\bf{あと}}\gt0\)なので、\(v_{\bf{あと}}=+6.0m/s\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}6m/s}\)
となります。
この手の問題は、\(v-t\)グラフを描き、加速度の定義式と(v-t)グラフの面積の式を立式することで解くことができます。
4.等加速度直線運動
等加速度直線運動とは、これまでに説明したように\(v-t\)グラフが直線(加速度の値が一定)である物体の運動となります。
変位・速度・加速度の解説で、平均の加速度と瞬間の加速度の説明をしましたが、\(v-t\)グラフの傾きが一定のときにはこの2つの値は同じになります。
※
平均の加速度は、あととはじめの点を結んだ直線の傾きであるが、傾き一定のためどこをあと、はじめにしても傾きは同じになる。
一方、瞬間の加速度もグラフの傾きが一定であるため、どこの点をみても傾きは同じになる。
等加速度直線運動には、公式と呼ばれるものが存在します。
これを\(v-t\)グラフから導出していきましょう。
(個人的には、加速度の定義式と面積の式で問題が解けるので、覚える必要はないと思いますが…)
\(\bf{[等加速度直線運動の公式]}\)
\(v=v_0+at\cdots①\)
\(\displaystyle{x=v_0t+\frac{1}{2}at^2\cdots②}\)
\(v^2-v_0^2=2ax\cdots③\)
上の公式中の\(v_0\)ははじめの速度、\(v\)はあとの速度のことです。
また、\(t_0\)ははじめの時間、\(t\)はあとの時間となります。
\((1)\)
加速度の定義式から、時刻\(t_0=0\)のとき\(①\)式を導く。
加速度の定義式は、
\(\displaystyle{a=\frac{v-v_0}{t-t_0}}\)
上式において、\(t_0=0\)のとき、
\(\displaystyle{\begin{eqnarray}&&a=\frac{v-v_0}{t-0}\\\\\Leftrightarrow&&at=v-v_0\\\\\Leftrightarrow&&v=v_0+at\end{eqnarray}}\)
となります。
\((2)\)
\(v-t\)グラフを用いて、\(v_0\gt0 , a\gt0\)のとき、\(②\)式を導く。
上記のとき、はじめの状態は\(t_0=0\)のとき\(v=v_0\gt0\)です。
そこから、加速度\(a\gt0\)なのでグラフは右上がりになります。
\(v-t\)グラフは以下のようになります。
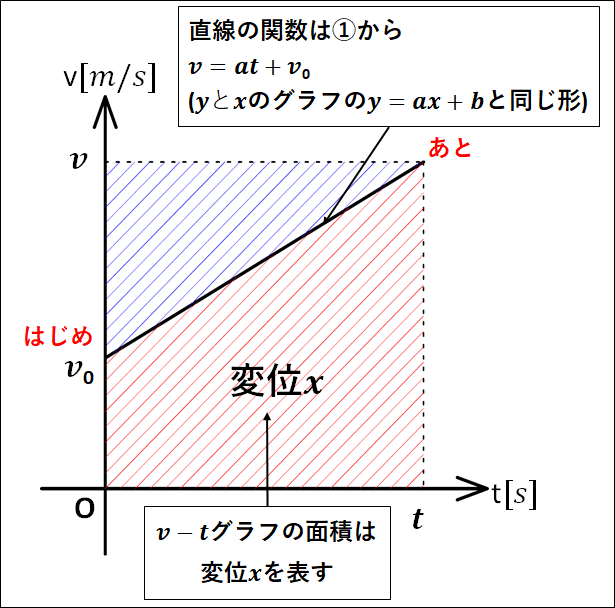
変位\(x\)は\(v-t\)グラフの面積なので、全体の四角形から青色の三角形の面積を引いて
\(\displaystyle{\begin{eqnarray}x&=&vt-\frac{1}{2}(v-v_0)t\\\\&=&\frac{1}{2}{2v-(v-v_0)}t\\\\&=&\frac{1}{2}(v+v_0)t\\\\&=&\frac{1}{2}(v_0+at+v_0)t (∵①)\\\\&=&\frac{1}{2}(2v_0+at)t\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となります。
※台形の面積、
\(({\bf{上底}}+{\bf{下底}})×{\bf{高さ}}÷2\)
を用いると、変位\(x\)部分は台形なので
\(\displaystyle{\begin{eqnarray}x&=&(v_0+v)×t÷2\\\\&=&\frac{1}{2}(v_0+v)t\\\\&=&\frac{1}{2}(v_0+at+v_0)t (∵①)\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となる。
\((3)\)
\(v-t\)グラフを用いて、\(v_0\gt0 , a\lt0\)のとき、\(②\)式を導く。
上記のとき、はじめの状態は\(t_0=0\)のとき\(v=v_0\gt0\)です。
そこから、加速度\(a\lt0\)なのでグラフは右下がりになります。
\(v-t\)グラフは以下のようになります。
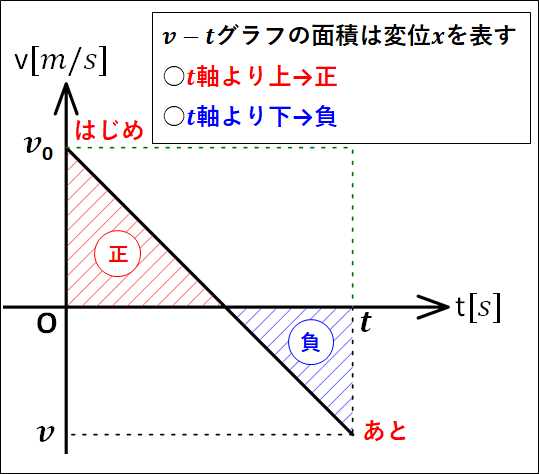
変位は、\(v-t\)グラフの面積であり、正の面積と負の面積の和となります。
したがって、正の面積から、負の面積の絶対値を引いたものとなります。
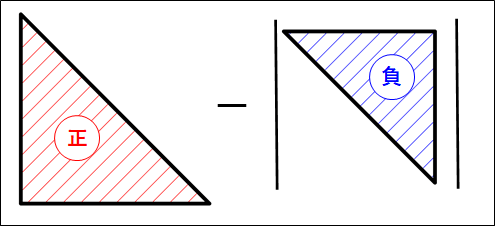
ここで、計算の工夫として、緑部分の面積を考えます。
緑部分の面積は共通なので、同じだけ足してから引いても計算結果は変わりません。
緑部分の面積を考慮すると、縦が\(v_0\)で横が\(t\)の長方形から、底辺が\(t\)で高さが\(v_0-v\)の三角形を引けばよいことが分かります。
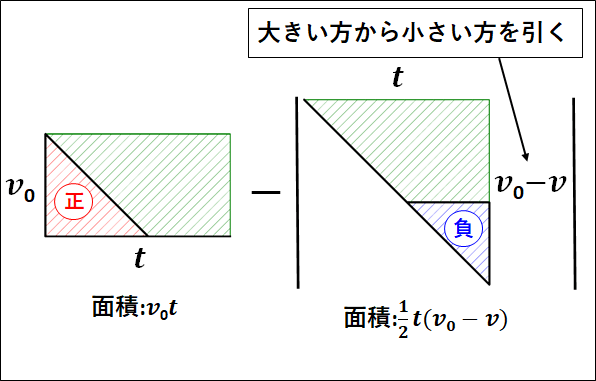
上記を計算すると、
\(\displaystyle{\begin{eqnarray}x=v_0t-\left|\frac{1}{2}t(v_0-v)\right|\end{eqnarray}}\)
ここで、\(t\)は正であり、\(v_0-v\)も正なので絶対値記号をとって
\(\displaystyle{\begin{eqnarray}x&=&v_0t-\left|\frac{1}{2}t(v_0-v)\right|\\\\&=&v_0t-\frac{1}{2}(v_0-v)t\\\\&=&\frac{1}{2}(2v_0-v_0+v)t\\\\&=&\frac{1}{2}(v_0+v)t\\\\&=&\frac{1}{2}(v_0+v_0+at)t (∵①)\\\\&=&\frac{1}{2}(2v_0+at)t\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となります。
\((4)\)
\(v-t\)グラフを用いて、\(①\)式から\(t\)を消去して\(③\)式を導く。\((v_0\gt0 , a\gt0)\)
\(①\)式から
\(\displaystyle{\begin{eqnarray}&&v=v_0+at\\\\\Leftrightarrow&&v-v_0=at\\\\\Leftrightarrow&&t=\frac{v-v_0}{a}\end{eqnarray}}\)
\((2)\)の\(v-t\)グラフから、変位\(x\)は三角形の面積なので
\(\displaystyle{\begin{eqnarray}&&x=\frac{1}{2}(v+v_0)t\\\\\Leftrightarrow&&x=\frac{1}{2}(v+v_0)×\frac{v-v_0}{a} (∵t=\frac{v-v_0}{t})\\\\\Leftrightarrow&&x=\frac{1}{2a}(v+v_0)(v-v_0)\\\\\Leftrightarrow&&x=\frac{1}{2a}(v^2-v_0^2)\\\\\Leftrightarrow&&2ax=v^2-v_0^2\\\\\Leftrightarrow&&v^2-v_0^2=2ax\end{eqnarray}}\)
となります。
\((5)\)
\(v-t\)グラフを用いて、\(①\)式から\(t\)を消去して\(③\)式を導く。\((v_0\gt0 , a\lt0)\)
\((4)\)と同様にして、\(①\)式から
\(\displaystyle{t=\frac{v-v_0}{a}}\)
\((3)\)の\(v-t\)グラフ面積から、変位\(x\)を計算して
\(\displaystyle{\begin{eqnarray}&&x=\frac{1}{2}(v+v_0)t (←(4)と同じ式)\\\\\Leftrightarrow&&v^2-v_0^2=2at\end{eqnarray}}\)
となります。
はてなブログ内関連記事
1.変位・速度・加速度
こちらでは、変位・速度・加速度の解説をしています。
また、速度と速さの違いや平均の速度と瞬間の速度の図形的意味、速度と加速度の定義式についても扱っています。
定義式については、問題を解くうえで何度も用いるので、しっかり覚えておく必要があります。
練習問題も別記事で用意しています。
問題を解くうえで、解説内容をどのように用いるのかや補足説明もしていますので、こちらの方にも目を通していただくようお願いします。
補足解説と練習問題の記事はこちらです。
→1-1.変位・速度・加速度(補足解説と練習問題)
サイトを設立しました。
こちらでも解説しているのでよろしくお願いします。
Twitterアカウント→@roke_blog
目次
1.変位と移動距離
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\bf{・変位は"あと"と"はじめ"で決まる}}\)
\(\textcolor{red}{\bf{・変位と移動距離の違い}}\)
\(\textcolor{red}{\bf{変位}}\)とは、物体がどちら向きにどれだけ移動したかを表す量となります。
また、向き(符合)と大きさがあるので、ベクトルとなります。
(ベクトルについてはこちら→ベクトルの演算と成分表示)
変位がどのように表されるかというと、
\(\displaystyle{\bf{変位=(あとの座標)-(はじめの座標)}}\)
で表されます。
特に、\(x\)座標上の物体の場合、
\(\displaystyle{\textcolor{green}{\begin{eqnarray}{\bf{変位}}&=&{\bf{(あとの}}{x}{\bf{座標)-(はじめの}}{x}{\bf{座標)}}\\\\&=&x_{\bf{あと}}[m]-x_{\bf{はじめ}}[m]\\\\&=&\Delta{x}[m]\end{eqnarray}}}\)
となります。
\(\Delta\)は(あと-はじめ、変化量)という意味になります。
上記の式は、\(\textcolor{green}{\bf{変位の定義となる}}\)ので、覚えるようにしましょう。
また、物体の位置は時間によって変わるので、\(x\)は時間\(t\)の関数となります。(\(x(t)\)と書く)
ベクトルである変位に対して、移動距離とは、移動した距離の合計であり、向きを持ちません。
したがって、符合は必ず正となりスカラーとなります。
例)
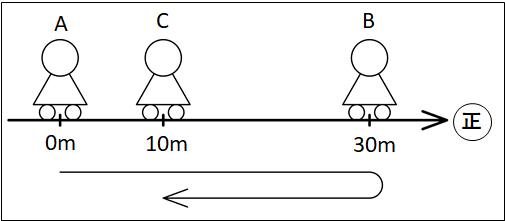
ある人が上図のように、\(A\)地点から\(B\)地点へと移動した後、\(C\)地点まで引き返したとします。(右向きを正とする)
このとき、変位は
(あとの\(x\)座標)=\(x_{\bf{あと}}\)=+\(10m\)
(はじめの\(x\)座標)=\(x_{\bf{はじめ}}\)=\(0m\)
なので、変位の定義から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}\Delta{x}&=&x_{\bf{あと}}-x_{\bf{はじめ}}\\\\&=&+10m-0m\\\\&=&+10m\end{eqnarray}}\)
となります。
今、右向きを正としているので、\(+10m\)の符合\(+\)は、正の方向を表しています。
すなわち、右向きに\(10m\)という意味になります。
また、移動距離は\(A→B\)までで\(30m\)、\(B→C\)までで\(20m\)移動しているので、
\(30m+20m=50m\)
となります。
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\bf{・変位は"あと"と"はじめ"で決まる}}\)
\(\textcolor{red}{\bf{・変位と移動距離の違い}}\)
2.速度と速さ
\(\textcolor{red}{\bf{速度}}\)とは単位時間あたりの変位で、こちらも向きと大きさをもつベクトルとなります。
単位時間の単位とは\(1\)という意味になります。
よって、単位時間というのは\(1\)秒や\(1\)分、\(1\)時間のことです。
※
\(1\)秒は\(1s\)とも書く。(\(s\)は\(second\)(秒)の頭文字)
\(1\)時間は\(1h\)とも書く。(\(h\)は\(hour\)(時間)の頭文字)
平均の速度\(\bar{v}\)の定義式は以下のようになります。
\(\displaystyle{\textcolor{green}{\bar{v}[m/s]=\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}}\)
上記は\(\textcolor{green}{\bf{平均の速度の定義となる}}\)ので、覚えるようにしましょう。
速度\(v\)は、\(velocity\)(速度)の頭文字です。
また、\(v\)の上についている\(-\)は平均という意味です。
定義式中の分子は\(x\)座標のあと-はじめなので変位となります。
分母は時間のあと-はじめになっています。
どちらもあと-はじめになっていることに注目しましょう。
あと-はじめ(変化量)という意味の\(\Delta\)(デルタ)を用いると、平均の速度の定義式は以下のようにも書けます。
\(\displaystyle{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}[m]}{\Delta{t}[s]}\end{eqnarray}}\)
速度\(v\)の単位は、距離\(m\)(メートル)を時間\(s\)(秒)で割っているので、\(m/s\)(メートル毎秒)となります。
(単位についてはこちら→単位の計算や換算(変換)方法)
向きと大きさをもつベクトルである速度に対して、この大きさにだけ注目したものが\(\textcolor{red}{\bf{速さ}}\)になります。
平均の速さを、平均の速度\(\bar{v}\)と絶対値記号を用いて表すと、
\({\bf{速さ}}=|\bar{v}|[m/s]\)
となります。
例)
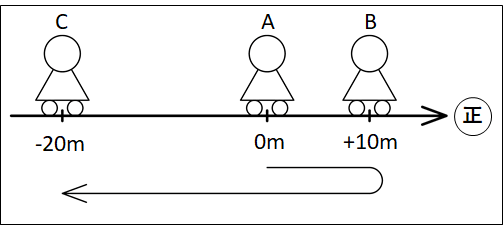
ある人が、上図のように(A→B→C)と(10)秒かけて移動したとします。
このときの、変位、移動距離、平均の速度、平均の速さを求めてみます。(右向きを正)
\(\bf(○変位)\)
はじめ(\(0\)秒のとき)、\(A\)地点にいるので\(x_{\bf{はじめ}}=0m\)
あと(\(10\)秒後)のとき\(C\)地点にいるので、\(x_{\bf{あと}}=-20m\)
以上より、変位の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}&=&x_{\bf{あと}}-x_{\bf{はじめ}}\\\\&=&(-20m)-(0m)\\\\&=&-20m\end{eqnarray}}\)
となります。
今右向きを正としているので、求めた変位についている符合のマイナスは左向きを表しています。
よって、左向きに\(20m\)ということもできます。
\(\bf{○移動距離}\)
移動距離は、\(A→B\)までで\(10m\)、\(B→C\)までで\(30m\)移動しているので
\(10m+30m=40m\)
となります。
\(\bf{○平均の速度}\)
はじめの地点とあとの地点の情報をまとめてみます。
\(A\)地点にいるときがはじめで、\(B\)地点にいるときがあとです。
はじめ:\(0s\)のとき、\(0m\)
あと:\(10s\)のとき、\(-20m\)
この情報と、平均の速度の定義式から
\(\displaystyle{\begin{eqnarray}\bar{v}&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}\\\\&=&\frac{-20m-0m}{10s-0s}\\\\&=&\frac{-20m}{10s}\\\\&=&-2.0m/s\end{eqnarray}}\)
となります。
今右向きを正としているので、符合マイナスの意味は左向きという意味になります。
よって、左向きに\(2.0m/s\)ともいえます。
\(\bf{○速さ}\)
速さは、速度の大きさなので(向き=符合の情報はもたない)
\({\bf{速さ}}=|\bar{v}|=|-2.0m/s|=2.0m/s\)
となります。
3.平均の速度と瞬間の速度のグラフ(図形)的意味
\(\textcolor{red}{\bf{○ポイント}}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・平均の速度}\\\\x-t{\bf{グラフのはじめの点とあとの点を結んだ直線の傾き}}}}\end{eqnarray}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・瞬間の速度}\\\\x-t{\bf{グラフのある点における直線の傾き}}}}\end{eqnarray}\)
先ほどみたように、平均の速度\(\bar{v}\)は
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}}{\Delta{t}}\end{eqnarray}}}\)
となります。
ここで、位置\(x[m]\)と時間\(t[s]\)の関係を表すグラフを考えてみます。(\(x-t\)グラフ)
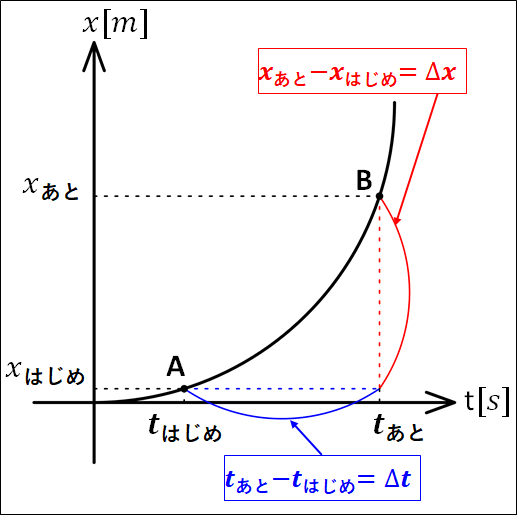
平均の速度\(\bar{v}\)は、
\(\displaystyle{\begin{eqnarray}\bar{v}[m/s]&=&\frac{\textcolor{red}{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}}{\textcolor{blue}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}\\\\&=&\frac{\textcolor{red}{\Delta{x}}}{\textcolor{blue}{\Delta{t}}}\\\\&=&\frac{\textcolor{red}{x{\bf{の変化量}}}}{\textcolor{blue}{t{\bf{の変化量}}}}\end{eqnarray}}\)
なので、これは点\(A\)と点\(B\)を結んだ直線の傾きとなります。
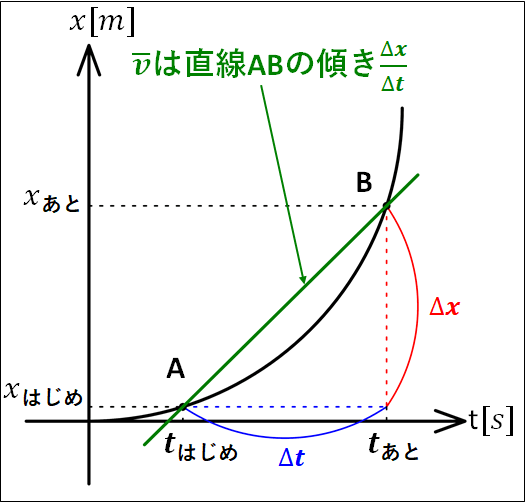
ここで、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に近づけていくと、\(x_{\bf{あと}}\)は\(x_{\bf{はじめ}}\)に近づいていきます。
このとき、直線\(AB\)の傾きも変化していきます。
瞬間の速度は、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に限りなく近づけたときの、接線の傾きになります。
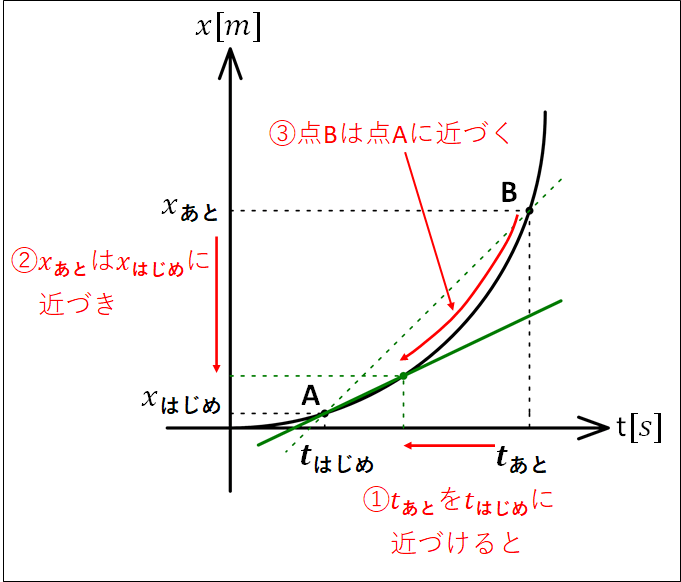
↓
ここで、\(t_{\bf{あと}}\)を限りなく\(t_{\bf{はじめ}}\)に近づけると、その傾きが瞬間の速度となる。
(点\(A\)における接線の傾きが瞬間の速度)
↓
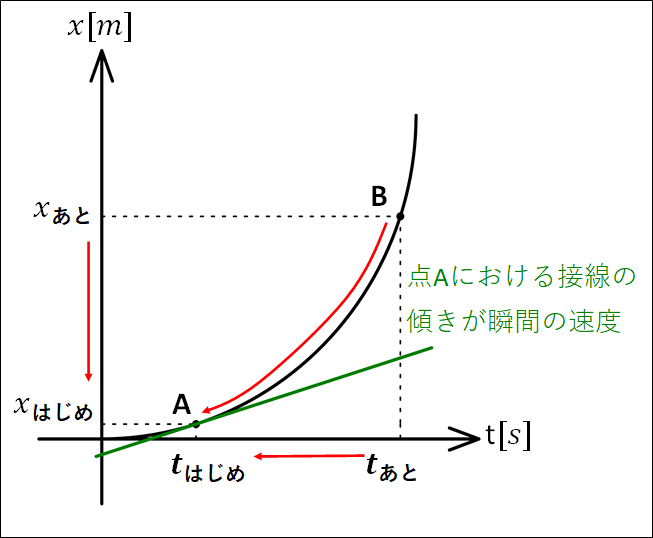
\(\textcolor{red}{\bf{○ポイント}}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・平均の速度}\\\\x-t{\bf{グラフのはじめの点とあとの点を結んだ直線の傾き}}}}\end{eqnarray}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・瞬間の速度}\\\\x-t{\bf{グラフのある点における直線の傾き}}}}\end{eqnarray}\)
※補足
数学的に…
平均の速度は
\(\displaystyle{\begin{eqnarray}\bar{v}&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}\\\\&=&\frac{\Delta{x}}{\Delta{t}}\end{eqnarray}}\)
ここで、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に限りなく近づけると、\(\Delta{t}\)は限りなく\(0\)に近づきます。
\(\Delta{t}\)を限りなく近づけるという記号である\(\displaystyle{\lim_{\Delta{t}\to0}}\)を用いると、瞬間の速度\(v\)は
\(\displaystyle{\begin{eqnarray}v&=&\lim_{\Delta{t}\to0}\bar{v}\\\\&=&\lim_{\Delta{t}\to0}\frac{\Delta{x}}{\Delta{t}}\\\\&=&\frac{dx}{dt}\end{eqnarray}}\)
となります。
これは数学でいう微分の考え方で、位置\(x\)を時間\(t\)で微分したものが瞬間の速度であるという意味になります。
(位置\(x\)は時間\(t\)の関数)
記号の感覚的には、\(\Delta{t}\)を限りなく\(0\)に近づけたので、
\(\displaystyle{\frac{dx}{dt}=\frac{{\bf{限りなく小さい}}x{\bf{のあと-はじめ}}}{{\bf{限りなく小さい}}t{\bf{のあと-はじめ}}}}\)
になります。
微分についてはこちらも参考にしてください
→微分係数と導関数
→微分法とその応用
4.加速度
物体が動いている方向に速度を加えていくと、物体はどんどん速くなります。
逆に、物体が動いている方向と逆向きに速度を加えていくと、物体はどんどん遅くなります。
\(\textcolor{red}{\bf{加速度}}\)とは、上記の速度を加えていくことに関して、単位時間(\(1\)秒間)あたりにどれだけ速度を加えるかを表す量となります。
また、加速度も向き(符合)と大きさをもつベクトルとなります。
平均の加速度\(\bar{a}\)の定義は以下のようになります。
(\(a\)は\(acceleration\)(加速度)の頭文字)
\(\displaystyle{\textcolor{green}{\bar{a}[m/s^2]=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m/s]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}}\)
となり、平均の速度の定義式の分子が位置\(x\)から速度\(v\)に変わったものになります。
分子は速度のあと-はじめ、分母は時間のあと-はじめとなります。
また、あと-はじめ(変化量)という意味の記号\(\Delta\)(デルタ)を用いて
\(\displaystyle{\bar{a}[m/s^2]=\frac{\Delta{v}[m/s]}{\Delta{t}[s]}}\)
とも表せます。
単位は、
\(m/s÷s=m/s^2\)(メートル毎秒毎秒)
となります。
瞬間の加速度は、瞬間の速度を考えたときと同様にして、時間の変化量\(\Delta{t}\)を(0)に近づけ
\(\displaystyle{a[m/s]=\lim_{\Delta{t}\to0}\frac{\Delta{v}[m/s]}{\Delta{t}[s]}=\frac{dv}{dt}[m/s^2]}\)
です。
速度\(v\)が位置\(x\)と時間\(t\)の関係を表す\(x-t\)グラフの傾きであったことと同様に、\(\textcolor{red}{\bf{加速度}}\)\(\textcolor{red}{a}\)\(\textcolor{red}{\bf{は速度}}\)\(\textcolor{red}{v}\)\(\textcolor{red}{\bf{と時間}}\)\(\textcolor{red}{t}\)\(\textcolor{red}{\bf{の関係を表す}}\)\(\textcolor{red}{v-t}\)\(\textcolor{red}{\bf{グラフの傾きを表しています}}\)
5.まとめ
\(\bf{[変位の定義]}\)
変位:
\(\textcolor{green}{\Delta{x}[m]=x_{\bf{あと}}-x_{\bf{はじめ}}}\)
(\(x\)軸上の運動の場合)
\(\bf{[速度の定義]}\)
○平均の速度
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}[m]}{\Delta{t}[s]}\end{eqnarray}}}\)
\(x-t\)グラフのあととはじめの点を結んだ直線の傾きを表す。
○瞬間の速度
\(\displaystyle{v[m/s]=\frac{dx}{dt}[m/s]}\)
\(x-t\)グラフのある点の接線の傾きを表す。
\(\bf{[加速度の定義]}\)
○平均の加速度
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{a}[m/s^2]&=&\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{v}[m/s]}{\Delta{t}[s]}\end{eqnarray}}}\)
\(v-t\)グラフのあととはじめの点を結んだ直線の傾きを表す。
○瞬間の加速度
\(\displaystyle{a[m/s^2]=\frac{dv}{dt}[m/s^2]}\)
\(v-t\)グラフのある点の接線の傾きを表す。
