物理と三角関数について2　三角関数のグラフ

サイトを設立しました。

こちらでも解説しているのでよろしくお願いします。

→三角関数の定義と関係式

Twitterアカウント→@roke_blog

○三角関数について2

今回は、前回に引き続き、三角関数のグラフについて書いていこうと思います。
こちらも参考にしていただけると有難いです。

物理と三角関数について1 三角関数の定義 - 高校物理理解の手助け

○三角関数のグラフについて

y=sinθや、y=cosθのグラフはどのようになっているのでしょう。
基本の形と、その説明を行っていきます。
単位円で考えると分かりやすいと思います。
下の画像のように、単位円周上の点Pは、角度θが変化していくと、円の上を回っていきます。
ここで、sinθは点Pのy座標、cosθは点Pのx座標なので、この座標の変化を図示したものがグラフの形です。

f:id:j-shindo:20190812161326j:plain

・y=sinθ

y=sinθのグラフは下の画像のようになります。

f:id:j-shindo:20190812161359j:plain

画像中の角度・θ・sinθの対応表は、sinθの値が特徴的な0、1、-1のものだけを載せています。
sinθは、単位円周上におけるy座標を表しているので、角度が0°から増えていくに従って、y座標も増えていきます。
角度が90°の点で値は最大の1となり、90°を過ぎるとsinθの値は減少していきます。
角度が270°の点で値は最小の1となり、270°を過ぎるとsinθの値は増大していき、360°で再び0 となります。

・y=cosθ

y=cosθのグラフは下の画像のようになります。

f:id:j-shindo:20190812161437j:plain

画像中の角度・θ・cosθの対応表も、cosθの値が特徴的な0、1、-1のものだけを載せています。
また、cosθは単位円周上のx座標を表していますが、y=cosθのグラフでは、cosθの値がy座標の値となるので、y=cosθの右側の単位円は、90°回転させています。
この画像中の単位円において、θが0°のときにはcosθは最大である1となります。
角度θが0°から増えていくに従って、cosθの値は徐々に減少していき、180°で最小の値-1となります。
角度が180°を超えると、cosθの値は徐々に増大していき、360°で再び最大値1となります。

・y=tanθ

y=tanθのグラフは下の画像のようになります。

f:id:j-shindo:20190812161505j:plain

角度が0°から増えていくと、原点と単位円周上の点を結んだ直線の傾きは右上がり(+)のまま徐々に増えていきます。
90°に近づくにつれて、大きくなっていき、最後は+∞となります。
ここで注意しなければならないのは、角度が90°及び-90°のときには、傾きが垂直となりtanθが定義できないということです。(tanθ= $\displaystyle \frac{c}{b}$ において、b=0となり分母が0となってしまう)
+∞になるというのは、角度が90°に近づくにつれて、画像中の式tanθ= $\displaystyle \frac{c}{b}$ におけるcは1に近づき、bは0に近づいていきます。
ほぼ90°の付近では、cはほぼ1、bはほぼ0なので簡単に考えれば $\displaystyle \frac{c}{b}$ = $\displaystyle \frac{0.99999999}{0.00000001}$ =0.99999999× $\displaystyle \frac{100000000}{1}$

のような状態であり、この後もさらに角度が90°に限りなく近づくにつれて分母は限りなく小さくなっていきます。
分母が小さくなるにつれて、tanθの値は大きくなっていき、+∞となります。
90°を超えると、傾きは右下がり(-)となるので、180°から90°へ限りなく近づく場合にはtanθの値は-∞となります。

次に、角度が0°から-90°へと近づいていく時を考えてみます。
原点と単位円周上の点を結んだ直線の傾きは右下がり(-)のまま徐々に増えていきます。(傾きはきつくなっていく)
ただし、-90°に限りなく近づいていくと、90°へ近づく時と同様の考え方で、tanθは-∞となり、-90°を超えた部分では、+∞となります。

f:id:j-shindo:20190812161540j:plain

○三角関数の周期

y=sinθやy=cosθ、y=tanθのグラフは、同じ形が繰り返してでてきます。
y=sinθとy=cosθでは、2πごとに、y=tanθではπごとに、同じ形が繰り返されます。
この、繰り返される形の間隔を周期といいます。
なので、y=sinθとy=cosθの周期は2πであり、y=tanθは周期がπとなります。

○振幅、周期など

上記の三角関数では簡単なものを扱いましたが、振幅や周期が上記とは異なるような関数になることもあります。
これから説明していくグラフについてですが、(θ-α)やkθが分かりやすい値となるようなθを考えて、表を作り、実際にグラフを書いてみると、どのようなグラフになるのか忘れてしまった時でも自分で導けると思います。

・振幅について

y=Asinθという関数について考えてみます。
上の関数において、Aを振幅といいます。
ですので、y=sinθやy=cosθのグラフはこの振幅Aが1の場合となります。
グラフでみてみると、y=sinθ、y=cosθの最大値はAとなります。
単位円で考えた場合は、半径Aの円周上の点のx座標とy座標がそれぞれ、AcosθとAsinθとなります。
以上のことから、y=Asinθやy=Acosθのグラフは、y=sinθ及びy=cosθのグラフをy軸方向にA倍したグラフとなります。
下にy=Asinθの画像を載せておきます。

f:id:j-shindo:20190812161613j:plain

・グラフの平行移動について

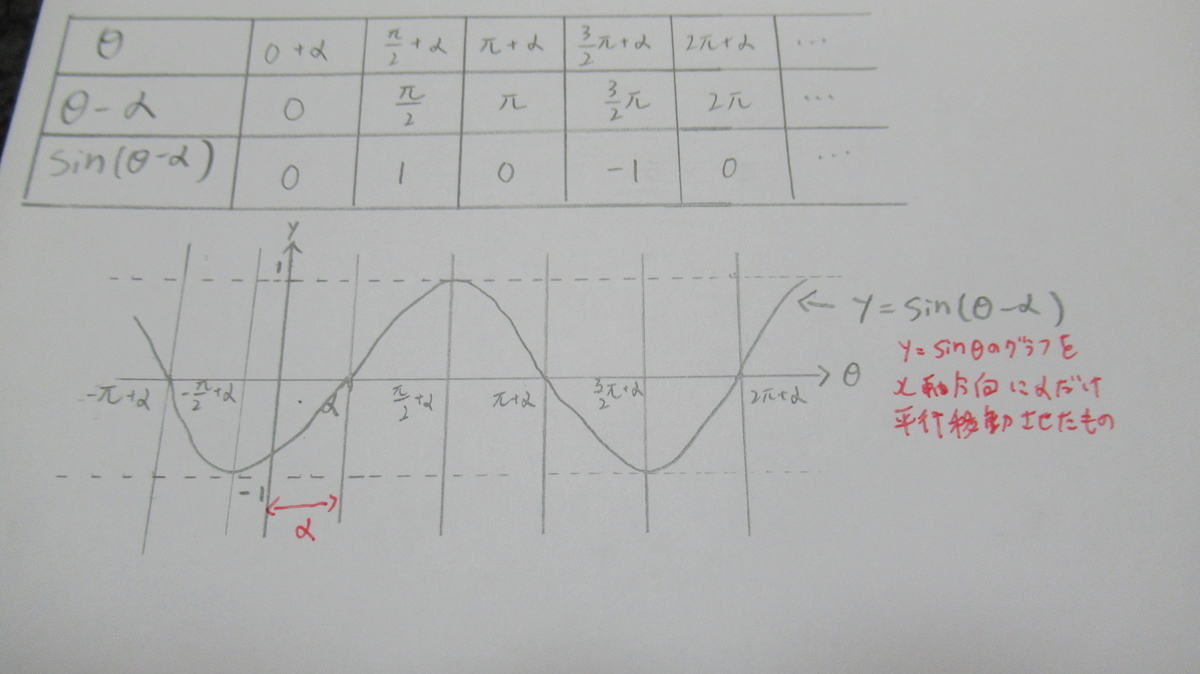
y=sin(θ-α)という関数について考えてみます。
この関数は、y=sinθのグラフをθ軸方向にαだけ平行移動させたものとなります。
y=cos(θ-α)のグラフも同様に、平行移動したものとなります。
参考として、y=sin(θ-α)のグラフの画像を載せておきます。
θとθ-αとsin(θ-α)の表とy=sin(θ-α)のグラフを実際に見ながらの方が分かりやすいと思います。
表のθの値は、(θ-α)が $\displaystyle \frac{π}{2}$ やπなどの分かりやすい値となるものを選んでいます。

f:id:j-shindo:20190812161646j:plain

・周期について

y=sinkxのグラフについて考えてみます。
これまでと同様に、表とグラフの画像を載せます。

f:id:j-shindo:20190812161738j:plain

表のθの値は、kθの値が分かりやすい値となるものを選んでいます。
画像の通り、y=sinkθのグラフは、y=sinθのグラフをθ軸方向に $\displaystyle \frac{1}{k}$ 倍したものとなっています。
ですので、周期も $\displaystyle \frac{1}{k}$ 倍されています。
これは、y=coskθのグラフについても同様です。
比較のために、y=sinθとy=sin2θのグラフを下に載せておきます。